Пример решения задачи №2

Пример решения задачи №1

Пример выполнения контрольной работы

Пусть задана следующая структурная схема системы (рис. 8.):

Рис.8

1.Используя правила преобразования структурных схем, определим эквивалентную передаточную функцию между точками “b” и “c”:

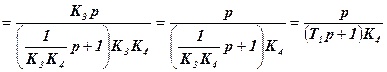, где T₁ = .

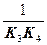2. Передаточная функция системы разомкнутой на главной обратной связи

3. Эквивалентная функция системы в замкнутом состоянии.

4. Передаточная функция ошибки относительно задающего воздействия:

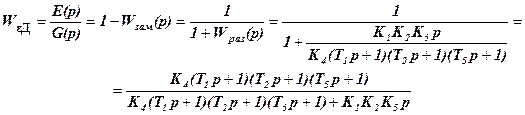
5. Передаточная функция системы относительно возмущения f(t) (точка приложения возмущения – вход)

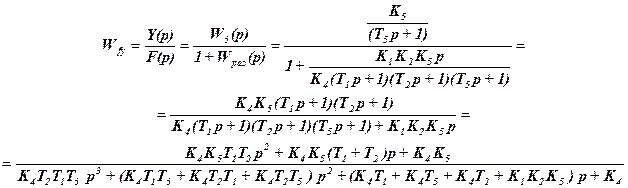
6. Изображение выходного сигнала: Y(p) = G(p) W_зам (p) + F(p) W_fy (p).

7. Уравнение системы в изображениях

,

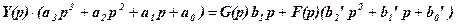где

8. Уравнение движения системы в дифференциальной форме

.

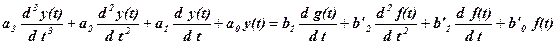Расчет устойчивости систем.

Рассчитать устойчивость системы, заданной следующей структурной схемой (рис.9) и построить кривую D-разбиения по коэффициенту усиления САУ в разомкнутом состоянии.

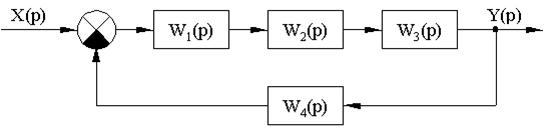
Рис. 9

W₁(P)=k₁; W₂(P)=;W₃(P)= 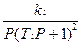; W₄(P)= .

Параметры звеньев: k₁=12; k₂=80; k₃=0.15; k₄=2; T₂=0.5; T₃=10; T₄=2.

1. Критерий Гурвица.

Запишем эквивалентную передаточную функцию системы

W_зам(р) = .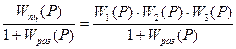

Запишем передаточную функцию системы, разомкнутой по главной обратной связи.

W_раз(p) = W₁(P) ×W₂(P) ×W₃(P) ×W₄(P) = .

Характеристическое уравнение системы.

D(p)=1+ W_раз(p)=0 ® D(p)=1+= 0;

K_э+(Т₂Т₃р³+Т₂р²+Т₄р+р)(Т₃²р²+2Т₃р+1)=0; Kэ=К₁К₂К₃К₄;

K_э + Т₂Т₄Т₃² р⁵ + (2Т₂Т₄Т₃ + Т₂Т₃² + Т₄Т₃²) р⁴ + (Т₄Т₂ + 2Т₂Т₃ + 2Т₄Т₃ + Т₃²) р³ +
(Т₂ + Т₄ + 2Т₃) р² + р = 0 ® .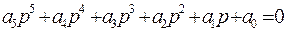

Подставляя численные значения, получаем:

.

Т.к. все коэффициенты положительны, то первое условие Гурвица выполняется.

Составим матрицу из коэффициентов характеристического уравнения и вычислим определители:

	22.5
		22.5

D₁=270>0; D₂=270•151-100•22,5=38520>0

		22.5
D3=				= 917325+0+7776000-0-72900-50625 = 8569800>0
			22.5

		22.5
D4 =					= – 7,96*10^8<0
		22.5

Ответ: Т.к. D₄ меньше нуля то система неустойчива.

2. Критерий Рауса.

Коэффициенты первого столбца таблицы должны быть положительны.

100р⁵+270р⁴+151 р³+ 22,5р⁴+ р+288=0

Таблица №8

№ п/п	Значение вспомогательного коэффициента	Столбец 1	Столбец 2	Столбец 3
	----------------
	----------------

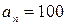
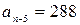
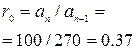
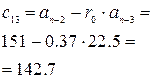
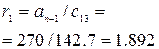
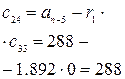
Ответ: Т.к. с₁₅<0, то система неустойчива.

3. Критерий Михайлова.

Уравнение характеристического вектора получим из характеристического уравнения заменой оператора р®jw.

D(p)= 100р⁵+270р⁴+151 р³+ 22,5р²+ р+288=0;

D(jw)=100(jw)⁵+270 (jw)⁴+151(jw)³+22,5(jw)²+jw+288 = 100jw⁵+270jw⁴-151jw³- -22,5jw²+jw+288 = (288-22.5w²+270w⁴)+jw(1-151w²+100w⁴)=Re(w)+Im(w).

Изменяя w в интервале 0<w<¥, рассчитываем Re(w) и Im(w) и заносим в таблицу №12.

Таблица №9

w		0.1	0.5				¥
Re		287.9		535.5			¥
Im		-0.05	-15.3	-50			¥

Т.к. годограф начинается на положительном отрезке вещественной оси (рис.14), но не обходит 5 квадрантов, то система неустойчива.

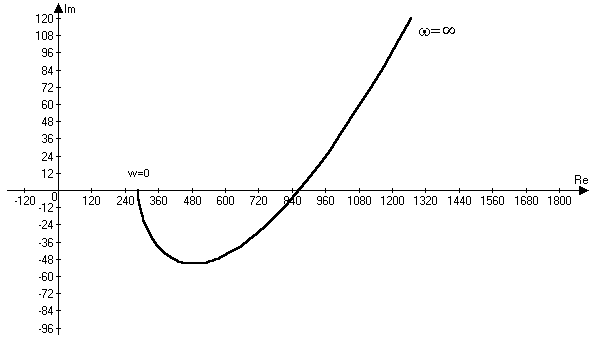Рис. 10

4. Критерий Найквиста.

Определяем устойчивость по АФЧХ системы, разомкнутой по главной обратной связи.

W_раз(p)= W₁(P)* W₂(P)* W₃(P) * W₄(P)=.

Комплексный коэффициент передачи САУ получим, заменяя p®jw

W_раз(jw)=.

Выведем действительную и мнимую части домножая числитель и знаменатель на комплексно-сопряженные множители.

;

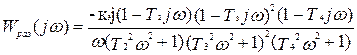Re=;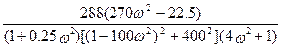
Im=.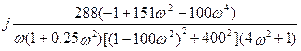

Задаваясь значениями w из промежутка 0 £ w < ¥, рассчитываем Re(w) и Im(w).

Таблица №10

w		0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9		¥
Re	-6336	-1334	-115	3,72	12,4	9,1	5,95	3,8	2,5	1,65	0,056
Im	-¥					12,2	5,33	2,43	1,13	0,52	-0,026

По данным таблицы строим АФЧХ системы (рис. 11).

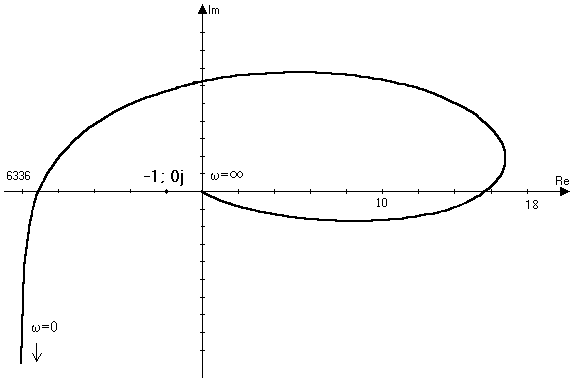
Рис. 11

Система неустойчива т.к. при дополнении годографа дугой с бесконечным радиусом до положительного отрезка вещественной оси АФЧХ охватывает критическую точку с координатами (–1; 0j).

Определим устойчивость, используя ЛАЧХ и ФЧХ системы.

Уравнение для построения ЛАЧХ системы:

20 lg|W(jw)| = 20 lgК_э – 20 lgw – 10 lg(1+T₂²w²) – 20 lg(1+T₃²w²) – 10 lg(1+T₄²w²)

20 lg K_э = 20 lg 288 = 49,19

Асимптотическую ЛАЧХ легко построить по ЛАЧХ типовых звеньев, суммируя их. Для этого рассчитывают частоты излома .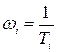

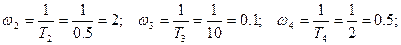
Уравнение для построения ФЧХ системы

j(w) = – 90 – arctg(wT₂) – 2 arctg(wT₃) – arctg(wT₄) =
= 90 – arctg(0,5w) – 2 arctg(10w) – arctg(2w).

Построим ФЧХ системы.

w		0.1	0.5		¥
j(w)	-90	-194	-306	-385	-450

САУ будет устойчива в замкнутом состоянии, если ЛАЧХ пересекает ось частот раньше, чем ФЧХ пересекает линию -180° (рис. 12.).

Значит система неустойчива.

Рис. 12

5. Метод D-разбиений по коэффициенту усиления.

100р⁵+270р⁴+151р³+22,5р²+р+288 = 0, К_сис= 288.

Выражаем коэффициент усиления системы из характеристического уравнения системы:

К_сис= -100р⁵-270р⁴-151 р³- 22,5р²- р.

Заменим p®jw

К_сис= -100(jw)⁵-270 (jw)⁴-151(jw)³-22,5(jw)²-jw =
-j100w⁵-270w⁴+j151w³+j22,5w²-jw = (-270w⁴ + 22.5w²)+j(-100w⁵ + 151w³ – w).

По этому выражению, изменяя 0<w<¥, строим кривую, которая затем дополняется зеркальным отображением относительно оси Х,и заштриховываем (рис. 13.) в соответствии с правилами.

Таблица №11

w		0,01	0,02	0,03	0,04	0,05	0,06	0,07
Re		0,002	0,009	0,02	0,035	0,055	0,078	0,104
Im		-0,01	-0,02	-0,03	-0,03	-0,03	-0,03	-0,02
w	0,08	0,09	0,1	0,2	0,3	0,4	0,5	0,6
Re	0,133	0,165	0,198	0,468	-0,16	-3,31	-11,3	-26,9
Im	-0	0,019	0,05	0,976	3,534	8,24	15,25	24,24
w	0,7	0,8	0,9		1,1	1,2	1,3	¥
Re	-53,8	-96,2	-159	-248	-368	-527	-733	-¥
Im	34,29	43,74	50,13		38,83	10,9	-40,8	-¥

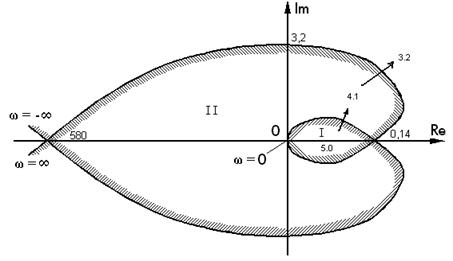
Рис. 13

Претендентом на область устойчивости является область 1.

Определим корни характеристического уравнения (определим устойчивость) при К, взятом из этой области, по критерию Гурвица.

100 р⁵ + 270 р⁴ +151 р³ + 22,5 р² + р + К=0

К=0.1 – получим все отрицательные корни.

Таким образом, САУ будет устойчива, если 0<K<0,14.

Критический коэффициент усиления системы можно определить, используя любой из критериев. D-разбиение позволяет выделить области с различным расположением корней характеристического уравнения на комплексной плоскости при изменении какого-либо параметра (в нашем случае К).

Дата добавления: 2014-10-23