
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
НИКОЛАЕВ, 2005. Разработано Ю.П. Кочановым
|
|
|
|
Разработано Ю.П. Кочановым
По выполнению расчетно-графической работы №1
Методические указания
Имени адмирала С.О.Макарова
Образования и науки Украины
М и н и с т е р с т в о
НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ КОРАБЛЕСТРОЕНИЯ
Кафедра СМК
по дисциплине «Математические модели и численные методы СМК»
«Расчет прямоугольной пластины при плоском напряженном состоянии»
1. С о д е р ж а н и е з а д а н и я. Для прямоугольной свободной подвешенной на кромках 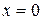 и
и  (рис.1) изотропной пластины, нагруженной по верхней кромке нормальными усилиями Р(х), определить:
(рис.1) изотропной пластины, нагруженной по верхней кромке нормальными усилиями Р(х), определить:
- перемещения v и нормальные напряжения σ х и σ у в сечении  ;
;
- перемещения u и касательные напряжения τ ху в сечении 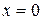 .
.
Вычислить указанные величины в пяти равноотстоящих точках по высоте поперечных сечений и построить эпюры. Сравнить полученные результаты с результатами расчета пластины по технической теории изгиба балок и сделать выводы.
Исходные данные:

t - толщина пластины;
a, b - размеры пластины (см. рис. 1);
Е - модуль Юнга,
μ = 0,3 - коэффициент Пуассона;
γ = b/a = 1; 1/2; 1/3; 1/4; 1/5; 1/6.
Погонная интенсивность нормальных усилий:
1) р(х)= 4 р0 ξ(1-ξ); ξ = х/a;
2) р(х)= р 0 sin 2πξ;
3) р(х)= 16 р 0ξ2(1-ξ)2;
4) р(х)= р 0.
Рис 1. Величины Е, b, t, р 0 считать заданными.
2. Указания по выполнению. На основании общего решения плоской задачи теории упругости для прямоугольной пластины [1,2], полученного методом разделения переменных выражения для компонентов напряженного состояния принять в виде:
 , (1)
, (1)
 , (2)
, (2)
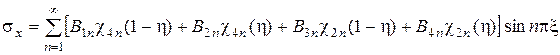 , (3)
, (3)
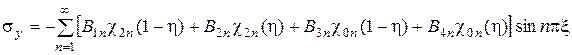 , (4)
, (4)
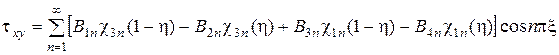 , (5)
, (5)
где 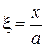 ;
;  ;
; 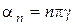 ;
; 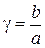 ; (6)
; (6)
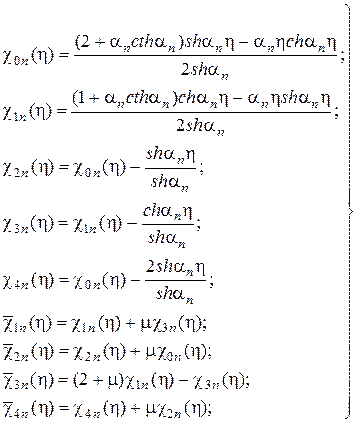 (7)
(7)
 - функции А.С. Калманка, подробные таблицы которых приведены в учебнике [2] и сокращенные в П.1.
- функции А.С. Калманка, подробные таблицы которых приведены в учебнике [2] и сокращенные в П.1.
Рекомендуется следующий порядок выполнения задания.
1. Записывается принятая форма решения (1-5), тождественно удовлетворяющая условиям жесткого подвеса на кромках пластины 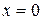 и
и  ;
;
2. Выписываются граничные условия на кромках пластины 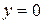 и
и ;
;
3. Решение (1-5) подчиняется граничным условиям на кромках 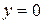 и
и ; в результате получается система уравнений для определения коэффициентов рядов
; в результате получается система уравнений для определения коэффициентов рядов 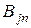 (
( = 1, 2, 3, 4);
= 1, 2, 3, 4);
4. Из системы п.3 определяются коэффициенты 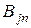 и подставляются в формулы (1-5);
и подставляются в формулы (1-5);
5. По формулам (1-5) вычисляются компоненты напряженно-деформированного состояния в соответствии с заданием в сечении 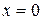 и
и  . Вычисления на ЭВМ выполнять при числе членов в рядах (1-5)
. Вычисления на ЭВМ выполнять при числе членов в рядах (1-5)  = 1, 3, 5, 7 и оценить сходимость результатов. Вручную вычислить максимальные значения при
= 1, 3, 5, 7 и оценить сходимость результатов. Вручную вычислить максимальные значения при  = 1:
= 1: 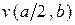 ,
, 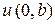 ,
,  ,
, 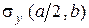 ,
, 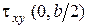 .
.
6. Строятся эпюры напряжений 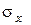 ,
,  ,
, 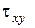 и перемещений
и перемещений 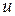 ,
, 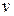 в заданных сечениях;
в заданных сечениях;
7. Находятся перемещения и напряжения рассматриваемой балки-стенки по технической теории изгиба балок под действием поперечной нагрузки
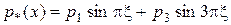 , (8)
, (8)
где 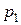 ,
,  - коэффициенты Фурье внешней нагрузки
- коэффициенты Фурье внешней нагрузки 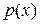 , представленной в виде ряда по синусам кратных дуг (см. ниже).
, представленной в виде ряда по синусам кратных дуг (см. ниже).
Решение по технической теории выполняется с учетом и без учета деформации сдвига. Сравниваются величины напряжений и перемещений, полученные на базе решений плоской задачи теории упругости (при  =3) и технической теории изгиба балок. Устанавливается погрешность технической теории изгиба балок с учетом и без учета деформации сдвига.
=3) и технической теории изгиба балок. Устанавливается погрешность технической теории изгиба балок с учетом и без учета деформации сдвига.
3. Справочные данные. Таблицы для функций А.С. Калманка приведены в учебнике [2] и приложении 1*. Расчет свободно опертой балки при действии на нее нагрузки (2) может быть выполнен с помощью таблиц изгиба балок [3], [4] или формул приложения 2.
Разложение внешней нагрузки 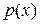 в ряд Фурье по синусам имеет вид:
в ряд Фурье по синусам имеет вид:
 (9)
(9)
где
 . (10)
. (10)
Для заданных четырех вариантов внешней нагрузки  коэффициенты Фурье (10) равны (при п =1, 3, 5…
коэффициенты Фурье (10) равны (при п =1, 3, 5… ):
):
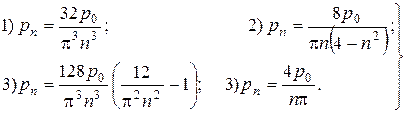 (11)
(11)
Коэффициенты  при
при  =2, 4, 6…
=2, 4, 6… равны нулю в силу симметрии заданных нагрузок относительно сечения
равны нулю в силу симметрии заданных нагрузок относительно сечения  .
.
Приложение 1.
Таблицы функций А.С. Калманка 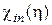 при
при  =1,
=1, 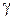 =1, 1/2, 1/3, 1/4, 1/5, 1/6.
=1, 1/2, 1/3, 1/4, 1/5, 1/6.
Таблица 1.
Значения функции 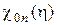
| η γ | 0,25 | 0,5 | 0,75 | 1,0 | |
| 0,0000 | 0,1488 | 0,3428 | 0,6234 | 1,0000 | |
| 1/2 | 0,0000 | 0,2330 | 0,4747 | 0,7308 | 1,0000 |
| 1/3 | 0,0000 | 0,2457 | 0,4937 | 0,7462 | 1,0000 |
| 1/4 | 0,0000 | 0,2485 | 0,4978 | 0,7484 | 1,0000 |
| 1/5 | 0,0000 | 0,2494 | 0,4991 | 0,7493 | 1,0000 |
| 1/6 | 0,0000 | 0,2497 | 0,4995 | 0,7497 | 1,0000 |
Таблица 2.
Значения функции 
| η γ | 0,25 | 0,5 | 0,75 | 1,0 | |
| 0,1798 | 0,2087 | 0,2947 | 0,4238 | 0,5136 | |
| 1/2 | 0,5894 | 0,6010 | 0,6325 | 0,6716 | 0,6935 |
| 1/3 | 0,9370 | 0,9416 | 0,9536 | 0,9681 | 0,9759 |
| 1/4 | 1,2649 | 1,2671 | 1,2727 | 1,2793 | 1,2828 |
| 1/5 | 1,5871 | 1,5882 | 1,5913 | 1,5948 | 1,5967 |
| 1/6 | 1,9072 | 1,9079 | 1,9097 | 1,9118 | 1,9129 |
Таблица 3.
Значения функции 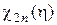
| η γ | 0,25 | 0,5 | 0,75 | 1,0 | |
| 0,0000 | 0,0736 | 0,1435 | 0,1708 | 0,0000 | |
| 1/2 | 0,0000 | 0,0579 | 0,0972 | 0,0920 | 0,0000 |
| 1/3 | 0,0000 | 0,0338 | 0,0552 | 0,0500 | 0,0000 |
| 1/4 | 0,0000 | 0,0210 | 0,0340 | 0,0304 | 0,0000 |
| 1/5 | 0,0000 | 0,0141 | 0,0228 | 0,0202 | 0,0000 |
| 1/6 | 0,0000 | 0,0101 | 0,0162 | 0,0143 | 0,0000 |
Таблица 4.
Значения функции 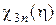
| η γ | 0,25 | 0,5 | 0,75 | 1,0 | |
| 0,0932 | 0,0940 | 0,0774 | -0,0371 | -0,4901 | |
| 1/2 | 0,1548 | 0,1326 | 0,0569 | -0,1010 | -0,3969 |
| 1/3 | 0,1366 | 0,1136 | 0,0410 | -0,0921 | -0,3050 |
| 1/4 | 0,1138 | 0,0936 | 0,0316 | -0,0774 | -0,2420 |
| 1/5 | 0,0956 | 0,0784 | 0,0256 | -0,0653 | -0,1990 |
| 1/6 | 0,0819 | 0,0669 | 0,0215 | -0,0561 | -0,1684 |
Таблица 5.
Значения функции 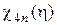
| η γ | 0,25 | 0,5 | 0,75 | 1,0 | |
| 0,0000 | -0,0017 | -0,0557 | -0,2819 | -1,0000 | |
| 1/2 | 0,0000 | -0,1171 | -0,2803 | -0,5469 | -1,0000 |
| 1/3 | 0,0000 | -0,1782 | -0,3833 | -0,6453 | -1,0000 |
| 1/4 | 0,0000 | -0,2065 | -0,4297 | -0,6876 | -1,0000 |
| 1/5 | 0,0000 | -0,2211 | -0,4535 | -0,7090 | -1,0000 |
| 1/6 | 0,0000 | -0,2295 | -0,4671 | -0,7211 | -1,000 |
Приложение 2.
Расчет пластины по технической теории изгиба балок.
При рассмотрении заданной пластины как балки необходимо принять (см. рис. 2):
- материал балки, такой же как у пластины;
- пролет балки равен 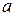 ;
;
- поперечное сечение - прямоугольник высотой 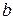 и шириной
и шириной  ;
;
- интенсивность поперечной нагрузки, определяется формулой (8);
- условия свободного подвеса пластины на кромках 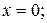 а соответствуют шарнирному опиранию балки на жесткие опоры.
а соответствуют шарнирному опиранию балки на жесткие опоры.
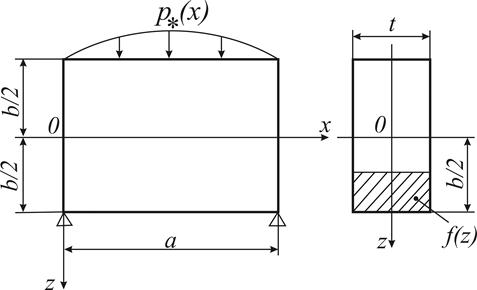
Рис. 2
Геометрические характеристики поперечного сечения будут:
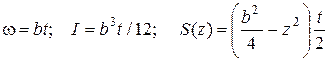 , (П.1)
, (П.1)
где
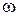 - площадь поперечного сечения;
- площадь поперечного сечения;
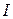 - центральный момент отсеченной площади;
- центральный момент отсеченной площади;
 - статический момент отсеченной площади
- статический момент отсеченной площади 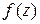 относительно нейтральной оси.
относительно нейтральной оси.
Определение прогиба балки сводится к решению краевой задачи:
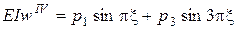 ; (П.2)
; (П.2)
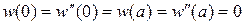 ; (П.3)
; (П.3)
Решение краевой задачи (П.2), (П.3) имеет вид:
 , (П.4)
, (П.4)
где
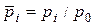 (П.5)
(П.5)
Прогиб от деформации сдвига будет:
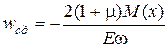 . (П.6)
. (П.6)
Изгибающий момент  и перерезывающая сила
и перерезывающая сила 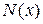 определяются по формулам:
определяются по формулам:

 . (П.7)
. (П.7)
Прогиб в сечении  равен:
равен:
- от изгиба
 ; (П.8)
; (П.8)
- от сдвига
 ; (П.9)
; (П.9)
- суммарный прогиб
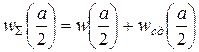 . (П.10)
. (П.10)
Нормальные напряжения 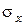 в сечении
в сечении  равны
равны
 . (П.11)
. (П.11)
В сечении  имеем:
имеем:
- перемещение точек вдоль оси 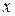 :
:
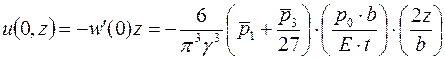 . (П.12)
. (П.12)
- касательные напряжения:
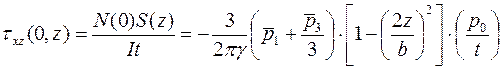 . (П.13)
. (П.13)
Формулы (П.8-П.13) получены на основании зависимостей (П.1), (П.4-П.7). Рекомендуется самостоятельно проверить указанные формулы.
Список литературы
1. Суслов В.П., Кочанов Ю.П. Задачник по строительной механике корабля и основам теории упругости. - Л.: Судостроение, 1977, с.216.
2. Суслов В.П., Кочанов Ю.П., Спихтаренко В.Н. Строительная механика корабля и основы теории упругости. - Л.: Судостроение, 1972, с.720.
3. Справочник по строительной механика корабля.Т.1.под ред. Ю.А.Шиманского. -Л.: Судпромгиз,1958, с.628.
4. Справочник по строительной механике корабля./Бойцов Г.В., Палий О.М., Постнов В.А., Чувиковский В.С. -Т.1. -Л.: Судостроение, 1982, с.376.
* Таблицы составлены на ПЭВМ П.В. Торондушем
|
|
|
|
Дата добавления: 2014-10-23; Просмотров: 229; Нарушение авторских прав?; Мы поможем в написании вашей работы!