Расчет тормозных устройств

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №9

Ленточные конвейеры с плоской и желобчатой лентой применяются для транспортирования сыпучих материалов и штучных грузов как в горизонтальной, так и в наклонной плоскостях.

К техническим параметрам унифицированного оборудования ленточных конвейеров относят ширину ленты, наибольшую скорость, диаметр приводного барабана, наибольший крутящий момент на валу.

Надежная и безопасная работа ленточного конвейера зависит от величины крутящего момента, максимального натяжения ленты, правильности выбора и эксплуатации тормоза.

Крутящий момент на валу определяют расчетным путем

Его значение должно быть примерно на 5 % меньше максимального крутящего момента. Максимальное натяжение ленты Sл рассчитывают по формуле

где Р - тяговое усилие на ободе, Н; Ко - коэффициент обхвата, его значение принимают по табл.10 N₁ - потребляемая мощность на валу приводного барабана кВт; 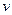- скорость движения ленты, м/с.

Необходимость установки тормоза выводят из неравенства 2N₀ > N₁. Если неравенство выполняется, то тормоз необходим:

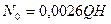
где Q - производительность конвейера, т/ч; Н - высота подачи груза, м.

Тормоз подбирают по моменту на валу приводного барабана от силы, движущей ленту вниз,

где п - частота вращения барабана, об/мин.

Значения коэффициента обхвата К₀

Пример 9.1. Требуется определить крутящий момент на валу, максимальное натяжение ленты, момент на валу приводного барабана от силы, движущей ленту вниз, и установить, на сколько процентов крутящий момент меньше максимального, требуется ли тормоз. Для решения задачи приведены следующие исходные данные N₁ = 1,6 кВт; n = 1500 об/мин; 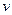= 0,925 м/с; атмосфера влажная производительность конвейера Q = 73 т/ч; высота транспортирования груза Н= 6 м.

Решение. Для заданных условии крутящий момент на валу по формуле

натяжение ленты по формуле (9.2)

мощность N_o - 0,0026·73·6 =1,13 кВт.

Тормоз в данном случае необходим, так как 2N₀ > N₁, т. е. 2·1,13 > 1,6.

Его необходимо подобрать по моменту М₁ на валу приводного барабана от силы, движущей ленту вниз,

Колодочные и ленточные тормоза в грузоподъемных механизмах получили наибольшее применение.

Взаимодействие различных сил в двух колодочном тормозе с грузовым замыканием показано на рисунке 9.1.

Рисунок 9.1 Расчетная схема двухколодочного тормоза

Обычно расчет тормоза с грузовым замыканием сводят к подбору электромагнита, подъемную силу которого определяют по формуле

где N - нормальное усилие, кгс; i - передаточное отношение тормоза (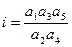 в расчетах принимают 1/16 -1/20); L - рабочее плечо электромагнита, м; q - вес якоря электромагнита, кгс.

С учетом к. п. д. 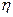электромагнита его подъемная сила должна быть равна 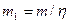. К.п.д. принимают в расчетах 0,94-0,96.

Допустимую массу удерживаемого груза можно oпpeделить из суммы моментов рычагов:

Пример 9.2. Установите, будет ли достаточным вес груза G = 10 кгс для следующих условий эксплуатации двухколодочного тормоза: i = 1/20; N = 100 кгс; l ₁ = 1 м.

Решение. Вес груза определяем по формуле (9.5)

Для приведения тормоза в положение торможения достаточен вес груза 5 кгс.

Потребный ход электромагнита h зависит от зазора, образованного при отходе колодок шкива 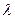коэффициента, учитывающего мертвые ходы С_о, передаточного отношения тормоза:

при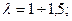Со = 1,1 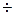1,2.

Пример 9.3. Определите подъемную силу для условий, приведенных в задаче 20. Другие данные имеют следующие численные значения: 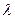= 1,4; Со = 1,2; q = 0,5 кгс; 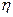= 0,95; L = 1,2.

Решение. Подъемную силу электромагнита определим по формуле (9.4)

а с учетом к.п.д. 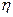=0,95

Колодки после подбора тормоза проверяют на удельную нагрузку

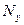- удельная нагрузка, мПа; 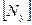- допускаемая удельная нагрузка, мПа (его значение принимают равным: чугун по чугуну 1; дерево по чугуну 0,3 - 0,6; феродо по чугуну 0,05 - 0,3); 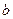- ширина колодки, м; 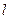- длина опорной поверхности колодки, м.

Пример 9.4. В процессе эксплуатации разрушилась колодка тормоза. Проверьте, не была ли превышена удельная нагрузка на ее при следующих условиях: 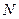= 100 кгс; рабочая поверхность чугунной колодки 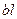= 6 см2.

Решение. Удельная нагрузка при заданных условиях составит

При трении чугунной колодки по чугунной опорной поверхности 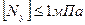. Следовательно, причиной разрушения колодки тормоза могло быть превышение удельной нагрузки.

Для определения массы груза или силы пружины -ленточных тормозов пользуются формулами: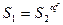

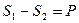
Решая совместно уравнения, получим:

S₁ и S₂ - натяжение соответственно набегающей и сбегающей

ветвей, Н; - основание натурального логарифма; a - угол обхвата шкива, рад; 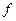- коэффициент трения скольжения; Р - окружное усилие, Н.

Значение 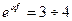, а величина окружного усилия может быть определена по формуле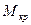- крутящий момент, Н·м; 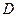- диаметр тормозного шкива, м; 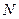- мощность привода, Вт; 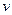- скорость, м/с.

На основании формул для расчета усилии S₁ и S₂ и условия взаимодействия сил в процессе торможения получены выражения для определения массы груза G, необходимого для торможения применительно к различным схемам тормозов:

простого ,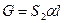

дифференциального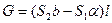

суммирующего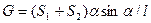

Пример 9.5. Определите натяжение набегающей ветви S₁ ленточного дифференциального тормоза и установите, не превышает ли оно предельно допустимое (16,5 кН) при следующих условиях: 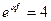; Р=12525Н.

Рисунок 9.2. Принципиальные схемы ленточных тормозов а - простого, б - дифференциального, в - суммирующего

Рисунок 9.3. Принципиальная схема пластинчатого тормоза: 1- пластина; 2- рукоятка тормоза; 3 – вал тормоза

Решение. Натяжение ленты определяют по формуле (9.8)

В данном случае может произойти обрыв ленты.

Ход электромагнита при отходе ленты от шкива, не пре­дающем 1 - 1,5 мм, должен быть для тормоза:

простого (9.11)

дифференциального (9.12)

суммирующего (9.13)

a, b, l, L - размеры, приведенные.

Пластинчатые тормоза (рисунке 9.3) приме­няют на всех электроталях, а также в других механизмах подъема. Особенность этих тормозов - компактность.

Расчет тормоза сводится обычно к определению размеров и числа пластин. Силу торможения определяют по заданному крутящему моменту 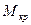Мкр, Н · м,

где 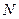- мощность, Вт; 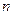- частота вращения, об/с.

Приняв во внимание, что 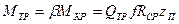, можно определить число пластин тормоза

где 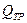- усилие торможения, задается при расчете тормоза, Н; Rср - средний радиус пластин, см; - коэффициент - отношение момента трения к крутящему моменту.Его значение принимают дифференцированно: для легкого режима - 1,75, среднего – 2, тяжелого - 2,5.

Тормозные прокладки проверяют на удельную нагрузку:

где F - площадь прокладки,

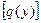- допускаемая удельная нагрузка, мПа; D₁ и D₂ - диаметры пластин, см.

Пример 9.6. Определите, будет ли превышена удельная нагрузка на пластины тормоза при следующих условиях: Мкр= 900 кгс·см; 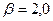; zп =6; f= 0,2;

D1 = 8; D2 = 12; 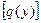= 4; Rср = 5.

Решение. Удельную нагрузку определяем, пользуясь формулам (9.14) и (9.15).

После подстановки исходных данных получим

Следовательно, в данном случае будет превышена допускаемая нагрузка на пластины тормоза.

Дата добавления: 2014-10-23