Подання періодичних несинусоїдних функцій рядом Фур’є

Для дослідження лінійних електричних кіл з періодичними несинусоїдними струмами доцільно ЕРС, напруги і струми подавати рядом Фур’є.

Будь-яка періодична функція f( ω t), яка відповідає умовам Діріхле (має протягом періоду скінченну кількість розривів 1-го роду і скінченну кількість екстремумів), може бути записана тригонометричним рядом Фур’є:

(7.1)

Тут: 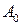– стала складова (нульова гармоніка);

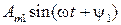– основна чи перша гармоніка;

– вища гармоніка k -го порядку;

– основна частота (кутова);

– період несинусоїдної функції.

Від форми ряду (7.1) легко перейти до іншої форми (7.2), врахувавши значення синуса суми ():

(7.2)

де

Коефіцієнти якщо функція f( ω t) задана аналітично на періоді (0, 2π), можуть бути визначені із співвідношень:

(7.3)

Якщо ж функція f( ω t) задана графічно і аналітичне рівняння функції невідоме, тоді замість обчислень за формулами (7.3) користуються чисельними розрахунками визначених інтегралів. Для цього період функції розбивають на р однакових інтервалів (р= 12, 24, 36у залежності від бажаної точності розрахунків) та визначають ординати функції в кінці кожного інтервалу (s набуває значень від 1 до р).

Виконавши відповідні зміни в формулах (7.3)

,

замість формул (7.3) отримаємо:

(7.4)

Визначивши коефіцієнти A ₀, B_k, C_k за формулами (7.3) чи (7.4), можемо записати функцію у вигляді ряду (7.2). Якщо ж є необхідність подати функцію у вигляді ряду (7.1), то попередньо визначають амплітуди A_mk і початкові фази всіх гармонік:

Для розрахунку електричного кола несинусоїдного струму зручніше користуватись формулою ряду (7.1).

В електротехнічних пристроях дуже часто зустрічаємо несинусоїдні періодичні струми і напруги, які відносять до категорії симетричних відносно осі абсцис функцій (рис 7.1 а). Такі функції мають задовольняти умову:

У ряді Фур’є такої функції не буде сталої складової і парних гармонік:

Важливою властивістю вказаних функцій є те, що для визначення коефіцієнтів B_k і C_k достатньо виконати інтегрування за півперіоду:

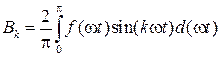, (7.5)

. (7.6)

Якщо функція симетрична відносно початку координат, тобто задовольняє умові 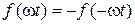(наприклад рис. 7.2 а), то ряд Фур’є такої функції містить тільки синусні складові:

.

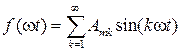Коефіцієнт A_mk ряду цієї функції може бути визначений інтегруванням за півперіоду за формулою (7.5) (A_mk= B_k).

Симетрична відносно осі ординат функція () не містить синусних складових і її ряд матиме вигляд:

.

Коефіцієнт A_mk цього ряду також може бути визначений інтегруванням за половину періоду ((7.6)).

Дата добавления: 2014-10-23