Интегрирование по частям

Пример 12.

Пример 10.

.

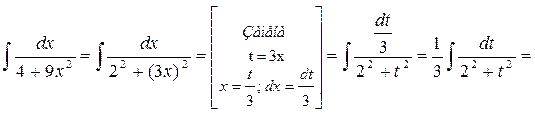
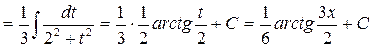Ответ: .

Пример 11.

.

Ответ: .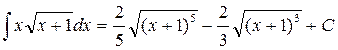

.

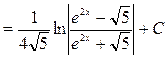Ответ: .

Пример 13.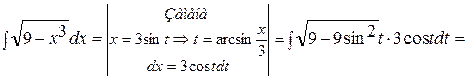

.

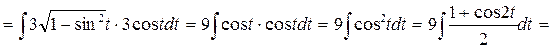
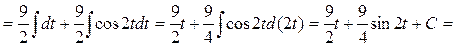
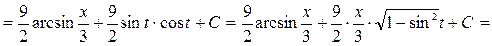
Ответ: .

Метод интегрирования по частям базируется на следующей теореме:

Теорема 2. Пусть функция U = U (x) и V = V (x) дифференцируемы на некотором интервале (a; b). Пусть на (a; b) функция V (x)× U ’(x) имеет первообразную. Тогда на (a; b) функция U (x)× V ’(x) также имеет первообразную. При этом справедливо равенство:

.

Доказательство. По форме дифференцирования:

(U (x)× V (x))’ = U ’(x)× V (x) + U (x)× V ’(x).

По свойству неопределенного интеграла:

.

Тогда можно записать:

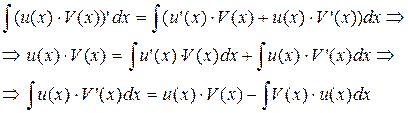
Замечание 1. Определение дифференциала и свойства инвариантности его формы позволяют переписать формулу интегрирования по частям в более короткой форме:

.

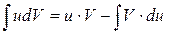Замечание 2. Для успешного вычисления интеграла необходимо разумно разбить подинтегральное выражение на два множителя u (x) и dV (x) так, чтобы интеграл 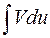оказался легко интегрируемым.

Практика показывает, что большая часть интегралов, берущихся с помощью метода интегрирования по частям может быть разбита на следующие три группы.

1) К первой группе относятся интегралы, у которых подынтегральная функция содержит в качестве множителя одну из следующих функций:

Ln x; arcsin x; arcos x; arctg x; arcctg x; ln² x; lnj(x); arcsin² x;…

при условии, что оставшаяся часть подынтегральной функции представляет собой производную известной функции.

Тогда за функцию u (x) берут соответствующую из перечисленных.

2) Ко второй группе относятся интегралы вида

, ,

, ,

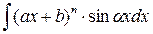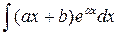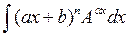где a,b,a,,A – некоторые постоянные числа, A > 0, n Î N.

При этом в качестве u (x) следует брать (ax + b) ⁿ и интегрировать по частям n раз.

3) К третьей группе относятся интегралы вида:

, , ,

, , ,

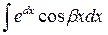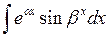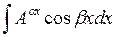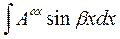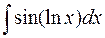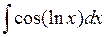где a, b, A – постоянные числа, A > 0, A # 1.

Такие интегралы берутся двукратным интегрированием по частям при любом выборе u (x). Это приводит к линейному уравнению относительно предложенного интеграла, откуда его и находят.

Замечание. Указанные три группы не исчерпывают всех без исключения интегралов, берущихся методом интегрирования по частям.

Дата добавления: 2014-10-15