Математическое выражение 2-го закона термодинамики. Три составляющие изменения энтропии термодинамической системы

Энтропия равновесного процесса S- это функция состояния и ее дифференциал dS- полный дифференциал

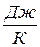, [] и , [].

Температура Т на границе ТС, где подводится теплота, есть интегрирующий делитель, превращающий неполный дифференциал – теплоту в полный дифференциал – энтропию. Для равновесного кругового процесса ∮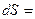∮- интеграл Клаузиуса.

У всякой ТС существует однозначная функция состояния – энтропия, которая при адиабатных равновесных процессах не изменяется.

Для сложной открытой ТС, которая взаимодействует с окружающей средой, изменение энтропии dS связано с подводом теплоты 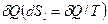, с протеканием процессов внутри ТС и с подводом массы вещества :

, Дж/К.

Для процессов, протекающих внутри ТС, 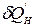- «некомпенсируемая теплота» (Клаузиус), в которую превращается количество работы вследствие необратимости (неравновесности) процессов внутри системы.

Если границу ТС пересекают несколько веществ с массами m_i, то изменение энтропии за счет ее подвода извне будет равно:

.

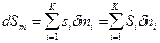Для обратимых процессов при подводе теплоты извне изменение энтропии ТС равно изменению энтропии окружающей среды с обратным знаком, т.е.

,

а в случае необратимых процессов

При протекании процессов внутри ТС энтропия может только расти, т.е. dS_in >0.

При этом количество энергии упорядоченного движения частиц, которое диссипировало в тепловую энергию, равно: 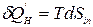. Тогда математическое выражение второго закона термодинамики для сложной открытой ТС примет вид:

,

где знак «=» для равновесных процессов, а знак «>» для неравновесных процессов.

Знак неравенства показывает, что изменение энтропии больше величины .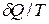

Для закрытой ТС dS_m =0 и математическое выражение 2-го закона термодинамики будет иметь вид:

.

Для неравновесного кругового процесса

∮, т.е. круговой интеграл по неравновесному пути не определяет изменение энтропии в круговом процессе (цикле), а меньше его. (Для равновесного кругового процесса ∮).

В качестве примера, характеризующего возрастание энтропии при неравновесных процессах, рассмотрим самопроизвольный переход теплоты от горячего тела №1 с температурой Т ₁ к холодному телу №2 с температурой Т ₂, приведя их в контакт и рассматривая систему из этих тел, как изолированную ТС, в соответствии со следующей схемой:

Изменение энтропии этой изолированной ТС будет равна сумме изменений энтропий тел №1 и №2 т.к. энтропия - величина аддитивная:

,

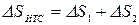или ,

где знак минус перед q/T₁ означает, что тело №1 отводит теплоту, а знак плюс перед q/T₂ означает, что к телу №2 подводится теплота.

Так как Т₁>Т₂, то , т.е. в результате неравновесного теплообмена энтропия ИТС возрастает.

Для равновесного перехода теплоты от тела №1 к телу №2 необходим посредник – термодинамическое рабочее тело (ТРТ), которое могло бы совершать обратимый цикл Карно, взаимодействуя с телами №1 и №2, как с источником теплоты и холодильником. Тело №3 – аккумулятор работы, который равновесно воспринимает от рабочего тела механическую работу. Тогда , где 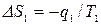, , 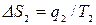, 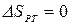т.к. совершив цикл, ТС возвращается в исходное состояние, и , т.к. тело №3 не участвует в теплообмене.

Тогда (с учетом знаков, принятых в термодинамике). Для цикла Карно известно, что термический коэффициент полезного действия цикла равен , или , т.е. сумма приведенных теплот цикла Карно равна нулю. Следовательно, изменение энтропии ИТС.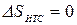

Дата добавления: 2014-10-23