Изохорный и изобарный тепловые эффекты химических реакций и связь между ними

Тепловой эффект химической реакции (ТЭХР) рассматривается только для закрытых ТС 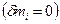при отсутствии работ 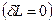и при фиксации двух параметров: T,V =const и T,p =const. При этих условиях мы фактически задаем состояние ТС, если система является равновесной.

Для простой, закрытой ТС уравнение 1-го закона термодинамики имеет вид:

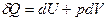, при Т,V =const: 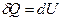, (1)

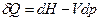, при Т,р =const: 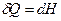. (2)

Тепловой эффект ХР – это максимальная теплота процесса, выделяемая или поглощаемая ТС при T,V =const и Т,р =const и отнесенная к пробегу ХР, т.е.:

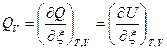, [Дж/моль], (3)

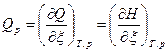, [Дж/моль], (4)

где Q_V – изохорный тепловой эффект ХР; Q_p - изобарный тепловой эффект ХР; 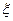- пробег ХР. Q_V и Q_p – функции состояния, т.е. они характеризуют термодинамическое состояние химически реагирующей ТС.

Таким образом, изохорный Q_V и изобарный Q_p ТЭХР выражаются через изменение внутренней энергии и энтальпии соответственно и определяются только начальными и конечными состояниями ТС.

Тепловые эффекты ХР не зависят от промежуточных химических состояний, через которые проходит ТС (закон Гесса, 1840г.).

В соответствии с законом Гесса сумма тепловых эффектов промежуточных ХР есть величина постоянная, равная тепловому эффекту сложной реакции независимо от последовательности протекания реакций. Закон Гесса позволяет косвенным путем аналитически вычислить тепловые эффекты ХР, в том числе и таких, которые не поддаются эксперименту.

Для ТС, где протекает одна химическая реакция, внутренняя энергия и энтальпия определяются выражениями:

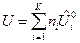, (5)

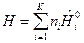, (6)

где 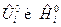, Дж/моль, молярные величины внутренней энергии и энтальпии i-го вещества при стандартном состоянии (р ⁰=1 физ.атм); 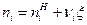, моль, количество i-го вещества.

Соотношения (5) и (6) справедливы как для идеальных, так и для реальных газов и растворов. Для идеальных термодинамических систем величины 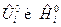являются функциями только температуры. Тогда получим связи:

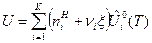, (7)

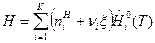. (8)

После подстановки выражений (7) и (8) в формулы (3) и (4) и дифференцирования по пробегу ХР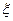получим формулы для расчета изохорного и изобарного ТЭХР:

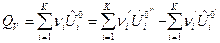, Дж/моль, (9)

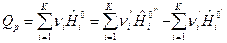, Дж/моль (10)

По формулам (9) и (10) определяется тепловой эффект образования вещества. Тепловой эффект сгорания (теплота сгорания) равен теплоте образования с обратным знаком:

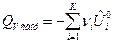, (11)

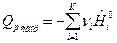. (12)

Рассмотрим пример: для ХР: 2Н₂О-2Н₂-О₂=0. Изобарный ТЭХР равен: 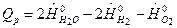, Дж/моль, т.е. из двух молекул Н₂ и одной молекулы О₂ образуется две молекулы воды. Если число элементарных реакций равно N_A=6,022·10²³, то суммарная теплота этих реакций является тепловым эффектом. Таким образом, моль – это набор из пяти частиц (2Н₂, О₂, 2Н₂О) умноженный на число Авагадро.

Если 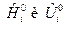зависят и от температуры и от состава ТС, то получим выражения:

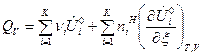, (13)

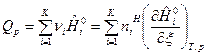. (14)

Связь между изобарным и изохорным ТЭХР получим следующим образом. Запишем для 1 моля идеального газа выражение для энтальпии:

.

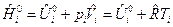Тогда для смеси идеальных газов имеем:

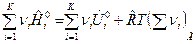, (15)

где ; .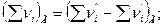

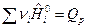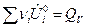После подстановки Q_p и Q_V в выражение (15) имеем:

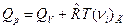. (16)

Эта связь между Q_p и Q_V для смеси идеальныхгазов получена, пренебрегая объемами жидких и твердых реагентов.

Зависимость 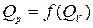определяется видом ХР:

- если 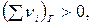то Q_p > Q_V

- если 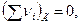то Q_p = Q_V

- если 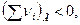то Q_p < Q_V.

Для конденсированных веществ (растворов) .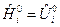

Дата добавления: 2014-10-23