
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Контрольная работа №1
|
|
|
|
ВАРИАНТЫ КОНТРОЛЬНЫХ РАБОТ ДЛЯ СЛУШАТЕЛЕЙ ЗАЧНОГО ОТДЕЛЕНИЯ
Решение примерного варианта КР №1
Примерный вариант контрольной работы №1
Задание 1
по разделу "Линейная алгебра"
1. Вычислить линейную комбинацию матриц А и В:
Дано: ,
, 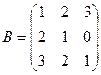 . Найти: 3А – 2В.
. Найти: 3А – 2В.
2. Вычислить произведение матриц:
а) .
.
б) 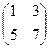
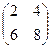 .
.
3. Найти матрицу, обратную данной: A=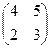 .
.
4. Вычислить определитель 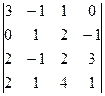 .
.
5. Вычислить ранг матрицы  .
.
6. Решить систему линейных уравнений с помощью формул Крамера:
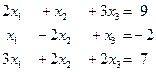 .
.
7. Методом Гаусса исследовать совместность и найти общее решение
системы:
а)
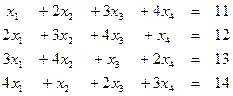 ;
;
б)
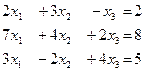 ;
;
в)

Задание 2
по разделу "Аналитическая геометрия"
1. Найти координаты и проверить коллинеарность векторов 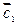 и
и 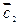 , построенных на векторах
, построенных на векторах 
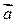 и
и 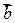 , если
, если  .
.
2. Найти косинус угла между векторами  и
и 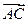 , если даны координаты точек:
, если даны координаты точек:
А (-1; 2; -3); В (3; 4; -6); С (1; 1; -1).
3. Вычислить площадь параллелограмма, построенного на векторах 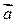 и
и 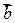 , если:
, если:
а).  ;
;
в) 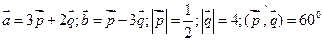 .
.
4. а) Составить уравнение стороны АС треугольника, если точки А (-3; 4) и В (2, 3) – его вершины, а М (1, 1) –точка пересечения его высот.
б)Составить уравнение прямой, проходящей через точку С, которая делит отрезок МК в отношении 1:3, параллельно прямой 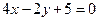 , если М (-3; 4), К (11,0).
, если М (-3; 4), К (11,0).
в) В треугольнике с вершинами А (-2; 0), В (2; 6) и С (4; 2) найти уравнение стороны АС, медианы ВЕ и высоты ВD.
Ответ: x – 3y + 2 = 0; 5x – y –4 =0; 3x + y – 12 = 0.
5. а) В эллипс вписана окружность 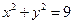 , пересекающая большую ось в фокусах, лежащих на оси OY. Составить уравнение эллипса. Сделать чертеж.
, пересекающая большую ось в фокусах, лежащих на оси OY. Составить уравнение эллипса. Сделать чертеж.
б) Составить уравнение окружности с центром в одной из вершин эллипса  и проходящей через фокус параболы
и проходящей через фокус параболы  . Сделать чертеж.
. Сделать чертеж.
в) Составить уравнение гиперболы, фокусы которой расположены на оси OY симметрично относительно начала координат, зная, что расстояние между фокусами равно 10, а угол между асимптотами кривой равен 600. Сделать чертеж.
Ответ: 4y2 – 12x2 = 75.
6. Написать разложение вектора x по базису p, q, r, если x = (11: –6: 5),
p = (3; –2; 1), q = (–1; 1; –2), r = (2; 1; –3).
Ответ: x = 2p – 3q +r.
Задание 1
по разделу "Линейная алгебра"
Задача 1. Вычислить линейную комбинацию матриц А и В.
Дано: ,
, 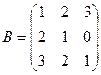 .
.
Найти: 3А – 2В.
Решение
1. Найдем 3А и 2В - произведения матриц на число, умножая каждый элемент матриц на соответствующее число:
 ;
;
 .
.
2. Вычислим поэлементно искомую разность полученных матриц:
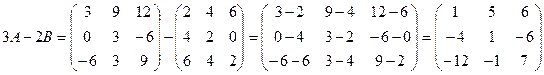 .
.
Ответ: 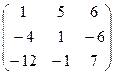 .
.
Задача 2. Вычислить произведение матриц:
а) .
.
Решение
1. Определим размер матрицы-произведения:  .
.
2. Найдем элементы сij матрицы-произведения как сумму произведений элементов i –ой строки матрицы А на соответствующие элементы j –го столбца матрицы В:
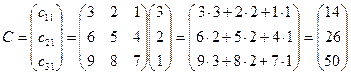 .
.
Ответ: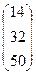 .
.
б) 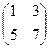
 .
.
Решение
1. Определим размер матрицы-произведения: 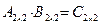 .
.
2. Найдем элементы сij матрицы-произведения С:
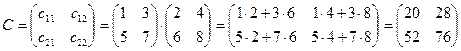 .
.
Ответ: 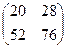 .
.
Задача 3. Найти матрицу, обратную данной: A=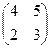 .
.
Решение
Для нахождения обратной матрицы воспользуемся формулой:
 , (1)
, (1)
где
detA - определитель матрицы А;
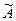 - присоединенная матрица, составленная из алгебраических дополнений элементов матрицы А;
- присоединенная матрица, составленная из алгебраических дополнений элементов матрицы А;
* - символ транспонирования матрицы.
1. Вычислим определитель матрицы:

Определитель матрицы 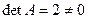 , следовательно, матрица А – невырожденная и обратная матрица
, следовательно, матрица А – невырожденная и обратная матрица 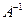 существует.
существует.
2. Составим присоединенную матрицу
 ,
,
где  - алгебраические дополнения,
- алгебраические дополнения, 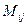 - миноры элементов матрицы А, связь между которыми выражается формулой:
- миноры элементов матрицы А, связь между которыми выражается формулой:
 . (2)
. (2)
Минор элемента определяется как определитель, получающийся из исходной матрицы вычеркиванием строки и столбца, на пересечении которых находится элемент.
3. Транспонируем матрицу 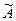 , т.е. поменяем местами строки и столбцы матрицы:
, т.е. поменяем местами строки и столбцы матрицы:
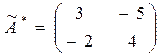 .
.
4. Вычислим обратную матрицу по формуле (1):
 .
.
5. Сделаем проверку. Согласно определению обратной матрицы
 , (3)
, (3)
где Е – единичная матрица.
Вычислим произведение  :
:
 .
.
Аналогично можно показать, что выполняется равенство 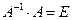 .
.
Ответ: 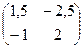 .
.
Задача 4. Вычислить определитель 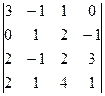 .
.
Решение
Для вычисления определителя четвертого порядка используем теорему о разложении определителя, согласно которой определитель n –го порядка Δ равен сумме произведений элементов какой-либо строки или какого либо столбца на их алгебраические дополнения, т.е.:
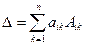 ,
,  ; (4)
; (4)
или
 ,
, 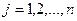 (5)
(5)
где 
 - алгебраические дополнения элементов; i – номер строки, j – номер столбца определителя Δ.
- алгебраические дополнения элементов; i – номер строки, j – номер столбца определителя Δ.
Разложим исходный определитель четвертого порядка (n = 4) по элементам второго столбца (j = 2), тогда формула (5) для вычисления определителя принимает вид:
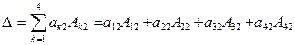 . (6)
. (6)
Пользуясь свойствами определителей, упростим вычисление определителя по формуле (6), обратив в нули все элементы второго столбца, кроме элемента  . Чтобы получить нули во втором столбце определителя, прибавим элементы первой строки (умноженные на 1) к соответствующим элементам второй и четвертой строк и вычтем из соответствующих элементов третьей строки:
. Чтобы получить нули во втором столбце определителя, прибавим элементы первой строки (умноженные на 1) к соответствующим элементам второй и четвертой строк и вычтем из соответствующих элементов третьей строки:
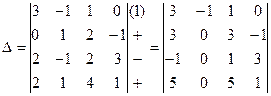 .
.
Вычисляя полученный преобразованный определитель по формуле (6), получим:
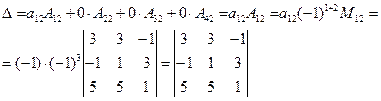
Таким образом, вычисление определителя четвертого порядка свелось к вычислению одного определителя третьего порядка, который можно вычислить, например, методом треугольников, а можно опять понизить порядок определителя, используя теорему разложения.
Применим второй способ, предварительно преобразовав определитель третьего порядка. Обратим в нули все элементы третьего столбца определителя, кроме элемента 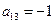 . Для этого сначала умножим все элементы первой строки на 3 и сложим их с соответствующими элементами второй строки, затем все элементы первой строки сложим с соответствующими элементами третьей строки.
. Для этого сначала умножим все элементы первой строки на 3 и сложим их с соответствующими элементами второй строки, затем все элементы первой строки сложим с соответствующими элементами третьей строки.
 .
.
Раскладывая определитель по элементам третьего столбца, и вынося общие множители, получим:
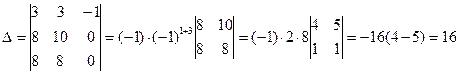 .
.
Ответ:16.
Задача 5. Вычислить ранг матрицы  .
.
Решение
1. Определим интервал, в котором находятся значения ранга данной матрицы. Известно, что для ранга матрицы А размера m x n справедливо соотношение:
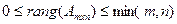 , (7)
, (7)
в соответствии с которым ранг исходной матрицы размера 3х4 лежит в интервале: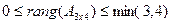 или
или 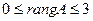 .
.
2. Для вычисления ранга матрицы воспользуемся методом элементарных преобразований, в соответствии с которым исходная матрица приводится к трапециевидной (ступенчатой) форме.
Приведем исходную матрицу к трапециевидной форме. Для этого на первом этапе получим нули в первом столбце матрицы, умножая элементы первой строки сначала на (-2), затем на (-5) и складывая их с соответствующими элементами второй и третьей строки:
 ®
® .
.
На втором этапе получим нули во втором столбце матрицы. Сначала для удобства дальнейших преобразований умножим элементы второй и третьей строки на (-1), а затем умножим элементы второй строки на (-2) и прибавим к соответствующим элементам третьей строки:
 .
.
Ранг полученной трапециевидной матрицы равен числу главных диагональных элементов (в данном случае – единиц), отличных от нуля, т.е. rang (A) = 2.
Ответ: 2.
Задача 6. Решить систему с помощью формул Крамера
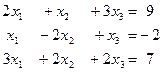 .
.
Решение
Формулы Крамера имеют вид:
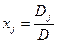 , (D ≠ 0; j = 1,2,…,n) (8)
, (D ≠ 0; j = 1,2,…,n) (8)
где
 - неизвестные, n – число неизвестных;
- неизвестные, n – число неизвестных;
D – главный определитель системы, составленный из коэффициентов при неизвестных,
Dj - вспомогательный определитель, получающийся из главного определителя D заменой j –го столбца на столбец свободных членов.
1. Вычислим определители (например, методом треугольников):
 - главный определитель;
- главный определитель;
вспомогательные определители
 ,
,  ,
,  .
.
2. Так как главный определитель системы отличен от нуля (D ≠ 0), то система имеет единственное решение, которое может быть найдено по формулам Крамера (8):
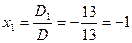 ,
,
 ,
,
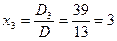 .
.
Целесообразно сделать проверку полученного решения. Подставим найденные значения неизвестных 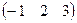 в исходную систему:
в исходную систему:
 .
.
При подстановке найденных значений неизвестных 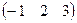 в исходную систему каждое уравнение системы обратилось в тождество, следовательно, найденная последовательность чисел
в исходную систему каждое уравнение системы обратилось в тождество, следовательно, найденная последовательность чисел 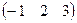 является решением системы.
является решением системы.
Ответ: 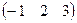 .
.
Задача 7. Решить методом Гаусса систему
а)
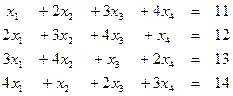 .
.
Решение
1. Определим число неизвестных системы n = 4 и число уравнений m = 4.
Выпишем матрицу коэффициентов системы 
и матрицу-столбец свободных членов 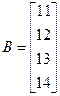 .
.
Составим расширенную матрицу системы 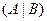 - матрицу коэффициентов, дополненную столбцом свободных членов
- матрицу коэффициентов, дополненную столбцом свободных членов
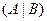 =
=  .
.
2. Приведем расширенную матрицу системы к трапециевидной форме (прямой ход метода Гаусса). Для этого, умножая элементы первой строки на числа (-2),(-3),(-4) и прибавляя их к соответствующим элементам второй, третьей, четвертой строки соответственно, получим нули в первом столбце матрицы. Затем, подбирая соответствующие множители ко второй и третьей строкам, получим нули во втором и третьем столбцах матрицы:
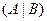 =
=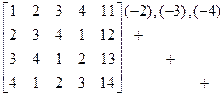 ®
®
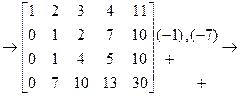
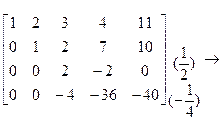
®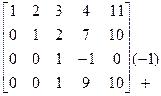 ®
®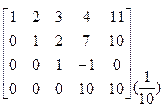 ®
®
3. [1]Определим ранги матриц:
rang  = rang
= rang  = 4 – ранг расширенной матрицы;
= 4 – ранг расширенной матрицы;
rang  =
=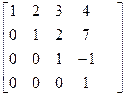 = 4 ранг матрицы коэффициентов системы.
= 4 ранг матрицы коэффициентов системы.
rang  = rang
= rang  = r = 4.
= r = 4.
Ранг матрицы коэффициентов системы равен рангу расширенной матрицы и равен числу неизвестных системы (r = n =4). В этом случае, согласно теореме Кронекера-Капелли, система имеет единственное решение.
4. Найдем решение системы (обратный ход метода Гаусса):
Запишем укороченную систему, соответствующую полученной трапециевидной матрице:
 .
. 
Найдем неизвестные, последовательно исключая переменные
из уравнения (4′) x 4 = 1,
из уравнения (3′) x 3 = 0+ x 4 = 0 + 1 = 1,
из уравнения (2′) x 2=10 – 2 x 3 – 7 x 4 = 10 – 2 – 7 = 1,
из уравнения (1′) x 1 = 11 – 2 x 2 – 3 x 3 – 4 x 4 = 11 – 2 – 3 – 4 = 2.
Ответ: система совместна, определена,
имеет единственное решение  .
.
б)
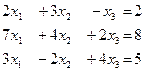 .
.
Решение
m = 3; n = 3.
1. Приведем расширенную матрицу системы к трапециевидной форме (прямой ход метода Гаусса):
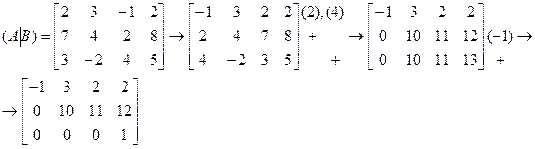 .
.
В процессе преобразований на первом шаге поменяли местами первый и третий столбцы матрицы; на втором и третьем шагах получили нули в первом и втором столбцах соответственно.
Исходя их вида полученной трапециевидной матрицы, можно сделать вывод о том, что система несовместна (т.е. не имеет решений), так как последняя строка матрицы содержит ненулевой свободный член и соответствует противоречивому уравнению, которое привело к неверному равенству 0 = 1.
Заметим, что в данном случае ранг расширенной матрицы не равен рангу матрицы коэффициентов системы rang  ≠ rang
≠ rang  и, в соответствии с теоремой Кронекера-Капелли, такая система несовместна.
и, в соответствии с теоремой Кронекера-Капелли, такая система несовместна.
Ответ: система несовместна.
в)
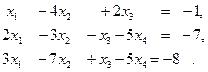
Решение
m = 3; n = 4.
Заметим, что в данном случае число уравнений меньше числа неизвестных (m < n), и такая система не может быть определена, т.е. не может иметь единственное решение.
1. Приведем расширенную матрицу системы к трапециевидной форме (прямой ход метода Гаусса):
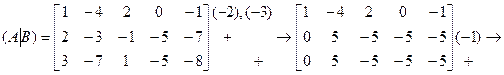
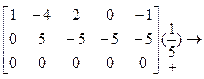
 .
.
2.Ранг полученной трапециевидной матрицы r, равный числу единиц, стоящих на главной диагонали, равен рангу матрицы коэффициентов системы, т. е. в этом случае
rang  = rang
= rang  = r = 2
= r = 2
и система совместна.
Так как r < n (ранг меньше числа неизвестных), система не определена, т.е. имеет бесконечное множество решений.
Так как r = 2, то две переменные х 1 и х 2, входящие в базисный минор, являются базисными, остальные (n – r) переменные – свободные.
Пусть свободные переменные х 3 и х 4 принимают произвольные числовые значения С1 и С2, т.е. положим:
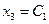
 .
.
3. Обратный ход метода Гаусса. Запишем укороченную систему, соответствующую полученной трапециевидной матрице:

Оставим базисные переменные х 1 и х 2 в левой части уравнений, а свободные переменные х 3 и х 4 перенесем в правую часть:
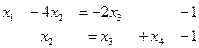 ,
,
где 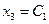 ;
;  ,
,
откуда

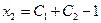 ,
,
 .
.
Запишем общее решение системы в виде вектор-функции от свободных переменных С1 и С2
 .
.
Ответ:  .
.
Задание 2
по разделу "Аналитическая геометрия"
Задача 1. Найти координаты и проверить коллинеарность векторов 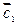 и
и 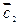 , построенных на векторах
, построенных на векторах 
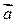 и
и 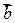 , если
, если  .
.
Решение.
1. Найдем координаты векторов 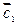 и
и 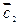 , выполняя линейные операции с векторами в координатной форме:
, выполняя линейные операции с векторами в координатной форме:
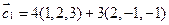 =
=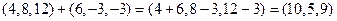 ;
;
 =
=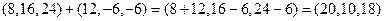 .
.
2. Условием коллинеарности векторов 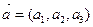 и
и 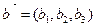 является пропорциональность их координат т.е.:
является пропорциональность их координат т.е.:
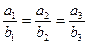
 ║
║ (9)
(9)
Проверим условие коллинеарности для векторов 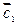 и
и 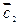 :
:


 ║
║ 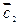 .
.
Координаты векторов пропорциональны, следовательно, векторы коллинеарны.
Убедиться в том, что векторы коллинеарны можно следующим образом: по условию
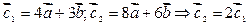 ,
,
т.е. выполняется условие 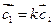 , где
, где  = 2, следовательно
= 2, следовательно  ║
║ 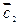 .
.
Ответ: векторы коллинеарны.
Задача 2. Найти косинус угла между векторами  и
и 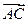 , если даны координаты точек: А (– 1; 2; – 3); В (3; 4; – 6); С (1; 1; – 1).
, если даны координаты точек: А (– 1; 2; – 3); В (3; 4; – 6); С (1; 1; – 1).
Решение
Косинус угла  между векторами
между векторами  и
и 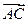 найдем по формуле
найдем по формуле
 , (10)
, (10)
где  - скалярное произведение векторов;
- скалярное произведение векторов;
 - модули векторов.
- модули векторов.
Скалярное произведение векторов 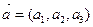 и
и 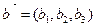 может быть вычислено по формуле:
может быть вычислено по формуле:
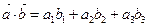 , (11)
, (11)
где  - координаты вектора
- координаты вектора  ;
; 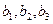 - координаты вектора
- координаты вектора  .
.
Модуль вектора  равен корню квадратному из суммы квадратов его координат, т.е.:
равен корню квадратному из суммы квадратов его координат, т.е.:
 . (12)
. (12)
1. Вычислим координаты векторов. Если вектор  задан координатами его конца (точка
задан координатами его конца (точка ) и начала (точка
) и начала (точка ), то координаты вектора определяются выражением:
), то координаты вектора определяются выражением:
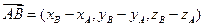 , (13)
, (13)
в соответствии с которым
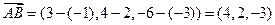 ;
;
 .
.
Найдем модули векторов  и
и 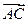 по формуле (12):
по формуле (12):
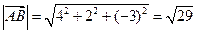 ;
; 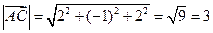 .
.
Вычислим скалярное произведение векторов (формула (11)):
 .
.
Подставим найденные значения в формулу (10) и вычислим косинус угла  между векторами
между векторами  и
и 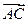 :
:
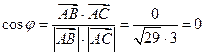 .
.
Ответ: 0.
Задача 3. Вычислить площадь параллелограмма, построенного на векторах 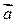 и
и 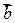 , если:
, если:
1)  ;
;
2)  .
.
Решение
Площадь параллелограмма, построенного на векторах 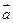 и
и 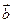 , может быть вычислена как модуль векторного произведения
, может быть вычислена как модуль векторного произведения 
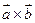 :
:
 . (14)
. (14)
По определению векторного произведения
 , (15)
, (15)
где φ – угол между векторами.
Если векторы 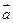 и
и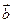 заданы своими координатами
заданы своими координатами
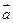 =
= 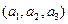 и
и 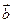 =
=  ,
,
то векторное произведение 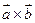 может быть вычислено с помощью определителя
может быть вычислено с помощью определителя
 . (16)
. (16)
1).  .
.
Векторы заданы своими координатами: 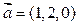 и
и 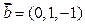 , поэтому для вычисления векторного произведения
, поэтому для вычисления векторного произведения 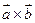 используем формулу (16), подставив в нее координаты векторов:
используем формулу (16), подставив в нее координаты векторов:
 =
= 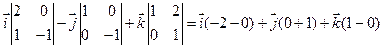 =
=
=  .
.
Найдем площадь параллелограмма (формула (14)), вычислив модуль вектора 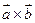 по формуле (12):
по формуле (12):
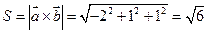 .
.
2).  .
.
В данном случае вычислим векторное произведение 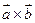 , используя свойства векторного произведения:
, используя свойства векторного произведения:
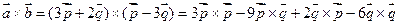 .
.
Так как  ,
,  ,
, 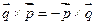 , получим
, получим
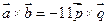 .
.
Найдем площадь параллелограмма (формула (14)), вычислив модуль векторного произведения 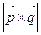 по формуле (15):
по формуле (15):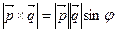 . В итоге получим:
. В итоге получим:
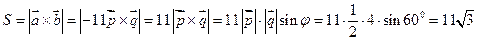
Ответ: 1)  ; 2)
; 2) 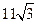 .
.
Задача 4.
а)Составить уравнение стороны АС треугольника, если точки
А(– 3; 4) и В(2, 3) – его вершины, а М (1, 1) – точка пересечения его высот.
Решение
1. Уравнение прямой, проходящей через две данные точки 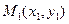 и
и  , имеет вид:
, имеет вид:
 . (17)
. (17)
Составим уравнение прямой ВМ как уравнение прямой, проходящей через две заданные точки В(2, 3) и М(1, 1), подставляя в уравнение (17) координаты точек B и М:
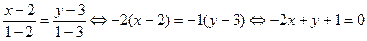 .
.
2. Уравнение прямой, проходящей через заданную точку  перпендикулярно данной прямой
перпендикулярно данной прямой 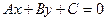 , имеет вид:
, имеет вид:
 . (18)
. (18)
Воспользуемся уравнением (18) и составим уравнение прямой АС как уравнение прямой, проходящей через заданную точку А(– 3; 4) перпендикулярно прямой ВМ, уравнение которой: 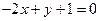 .:
.:
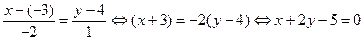 .
.
Полученное уравнение может быть проверено.
Во-первых, можно проверить, проходит ли полученная прямая через точку А. Для этого достаточно подставить координаты точки А (– 3; 4) в полученное уравнение прямой АС и убедиться в том, что координаты точки А удовлетворяют этому уравнению: 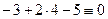 .
.
Во-вторых, можно проверить, выполняется ли условие перпендикулярности прямых АС и BM.
Условие перпендикулярности прямых, заданных общими уравнениями вида 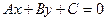 , имеет вид:
, имеет вид:
 , (19)
, (19)
т.е. условием перпендикулярности прямых является равенство нулю суммы произведений коэффициентов при переменных в уравнениях прямых.
Убедимся в перпендикулярности прямой АС: 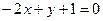 и прямой BM:
и прямой BM:  , подставляя в условие (19) соответствующие коэффициенты:
, подставляя в условие (19) соответствующие коэффициенты: 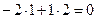 .
.
Ответ: 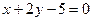 .
.
б)Составить уравнение прямой, проходящей через точку С, которая делит отрезок МК в отношении 1:3, параллельно прямой 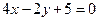 , если М (-3; 4), К (11,0).
, если М (-3; 4), К (11,0).
Решение
1. Координаты точки С, которая делит отрезок М1М2 в данном отношении λ, определяются формулами:
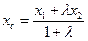 ;
; 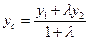 (20)
(20)
где 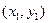 - координаты точки М1- начала отрезка;
- координаты точки М1- начала отрезка; 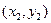 - координаты точки М2 –конца отрезка.
- координаты точки М2 –конца отрезка.
В нашем случае λ = 1/3, 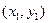 = (- 3,4);
= (- 3,4); 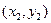 = (11,0). Подставляя эти значения в формулу (20), определим координаты точки С:
= (11,0). Подставляя эти значения в формулу (20), определим координаты точки С:
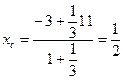 ;
; 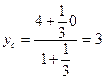 .
.
Итак, точка С имеет координаты (1/2, 3).
2. Уравнение прямой, проходящей через заданную точку  параллельно данной прямой
параллельно данной прямой 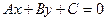 , имеет вид:
, имеет вид:
 . (21)
. (21)
С помощью уравнения (21) составим уравнение прямой, проходящей через точку С(1/2, 3) параллельно прямой 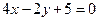 :
:
 , или
, или 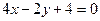 , или
, или  .
.
3. Условием параллельности прямых, является пропорциональность коэффициентов при переменных в общих уравнениях прямых, т.е.:
 (22)
(22)
Проверим, выполняется ли условие параллельности (22) для прямых 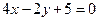 и
и  :
: 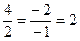 .
.
Ответ:  .
.
в) В треугольнике с вершинами А(-2; 0), В(2; 6) и С(4; 2) найти уравнение стороны АС, медианы ВЕ и высоты ВD.
Решение
1. Составим уравнение прямой АС как уравнение прямой, проходящей через две заданные точки А(-2; 0), и С(4; 2) подставляя в уравнение (17) координаты точек А и С:
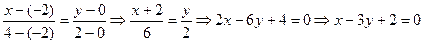 .
.
2. Воспользуемся уравнением (18) и составим уравнение прямой BD как уравнение прямой, проходящей через заданную точку В(2; 6) перпендикулярно прямой AC, уравнение которой 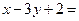 0:
0:
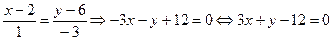 .
.
3. Определим координаты точки Е, как координаты середины отрезка АС. Формула для определения координат середины отрезка может быть получена из формулы (20) при λ = 1:
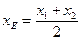 ;
; 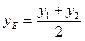 , (20)
, (20)
где 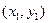 , - координаты точки А - начала отрезка;
, - координаты точки А - начала отрезка; 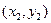 - координаты точки С – конца отрезка.
- координаты точки С – конца отрезка.
Подставляя в (20) координаты точек А(-2; 0) и С(4; 2), вычислим координаты точки Е:
 ;
;  , т.е. Е(1,1)
, т.е. Е(1,1)
4. Составим уравнение медианы BE как уравнение прямой, проходящей через две заданные точки В(2; 6), и Е(1,1) подставляя в уравнение (17) координаты точек B и E:
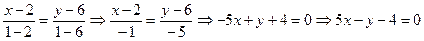 .
.
Ответ: x – 3 y + 2 = 0; 5 x – y –4 =0; 3 x + y – 12 = 0.
Задача 5.
а) В эллипс вписана окружность 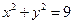 , пересекающая большую ось в фокусах, лежащих на оси OY. Составить уравнение эллипса. Сделать чертеж.
, пересекающая большую ось в фокусах, лежащих на оси OY. Составить уравнение эллипса. Сделать чертеж.
Решение
1. Сделаем чертеж (см. рис.1).
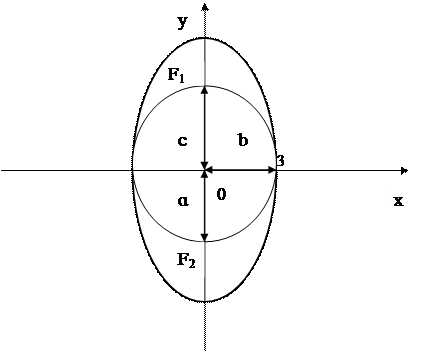
Рис.1. Чертеж к задаче 5а.
2. Уравнение 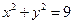 описывает окружность с центром в начале координат, радиус которой
описывает окружность с центром в начале координат, радиус которой 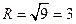 .
.
3. По условию задачи фокусы эллипса лежат на оси OY, тогда малая полуось эллипса лежит на оси ОХ и равна радиусу вписанной окружности, т.е. 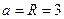 .
.
4. Окружность пересекает большую ось в фокусах эллипса, тогда фокусное расстояние равно радиусу окружности 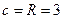 .
.
5. Найдем  (квадрат большой полуоси эллипса) из соотношения
(квадрат большой полуоси эллипса) из соотношения  :
:
 .
.
6. Составим уравнение эллипса, воспользовавшись каноническим уравнением эллипса:
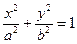 , (23)
, (23)
Подставляя в уравнение (23)  = 9,
= 9,  =18, получим:
=18, получим:
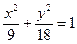 .
.
Ответ: 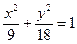 .
.
б) Составить уравнение окружности с центром в одной из вершин эллипса  и проходящей через фокус параболы
и проходящей через фокус параболы  . Сделать чертеж.
. Сделать чертеж.
Решение
1. Определим параметры и построим эллипс, описываемый уравнением  . Сравнивая данное уравнение с каноническим уравнением эллипса (23) найдем:
. Сравнивая данное уравнение с каноническим уравнением эллипса (23) найдем:
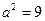 ;
; 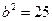
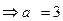
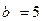 - полуоси эллипса.
- полуоси эллипса.
Определим вершины эллипса как точки пересечения эллипса с осями координат: A1(-3,0), A2(3,0), B1(0,5), B2(0,-5) (см. рис.2).
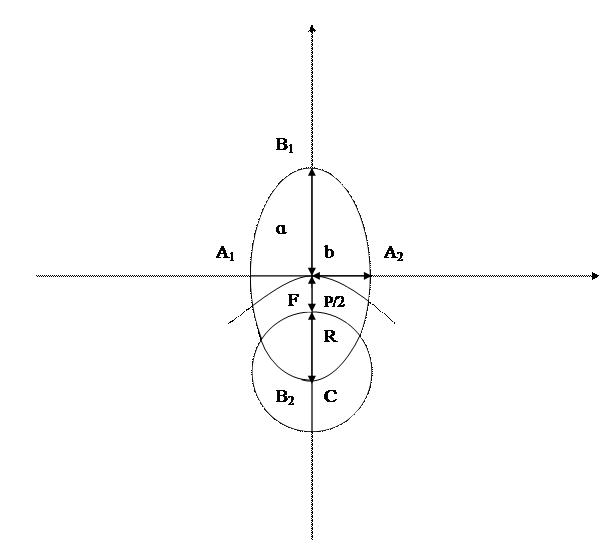
Рис. 2. Чертеж к задаче 5б.
2. По уравнению параболы  определим параметры и построим кривую.
определим параметры и построим кривую.
Каноническое уравнение параболы имеет вид:
 (24)
(24)
где p – параметр параболы.
Записывая уравнение  в виде
в виде  , и сравнивая полученное уравнение с каноническим уравнением (24), определим параметр параболы:
, и сравнивая полученное уравнение с каноническим уравнением (24), определим параметр параболы: 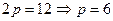 .
.
Парабола, описываемая уравнением (24), проходит через начало координат (точка (0,0) – вершина параболы) и лежит в нижней полуплоскости (y ≤ 0).
Фокус параболы (24) - точка F с координатами (0,  )., следовательно, фокусом параболы
)., следовательно, фокусом параболы  является точка F(0,-3).
является точка F(0,-3).
3. Каноническое уравнение окружности радиуса R с центром в точке С( ) имеет вид:
) имеет вид:
 . (25)
. (25)
По условию задачи центр окружности лежит в одной из вершин эллипса. Выберем центр окружности в вершине эллипса B2(0,-5), тогда координаты центра окружности 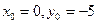 , а радиус окружности
, а радиус окружности 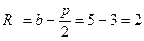 . Подставляя полученные данные в (25), получим искомое каноническое уравнение окружности:
. Подставляя полученные данные в (25), получим искомое каноническое уравнение окружности:
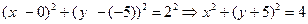 .
.
Ответ: x 2 + (y +5)2 = 4.
в) Составить уравнение гиперболы, фокусы которой расположены на оси OY симметрично относительно начала координат, зная, что расстояние между фокусами равно 10, а угол между асимптотами кривой равен 600. Сделать чертеж.
Решение
1. Каноническое уравнение гиперболы, фокусы которой расположены на оси OY симметрично относительно начала координат, имеет вид:
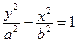 , (26)
, (26)
где  и b – вещественная и мнимая полуоси гиперболы соответственно, которые в данной задаче являются неизвестными (чертеж см. на рис.3).
и b – вещественная и мнимая полуоси гиперболы соответственно, которые в данной задаче являются неизвестными (чертеж см. на рис.3).

Рис. 3. Чертеж к задаче 5в.
2. Для нахождения двух неизвестных составим систему из двух уравнений.
Для гиперболы
 , (27)
, (27)
где с – фокусное расстояние.
По условию задачи 2с = 10, с = 5, тогда из (27) получим первое уравнение:
 .
.
Обозначим угол между асимптотами α. По условию задачи α = 600. Рассматривая главный прямоугольник гиперболы, найдем тангенс угла α/2:
 , или
, или  , откуда получим второе уравнение системы
, откуда получим второе уравнение системы
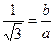 .
.
3. Решая систему, получим:



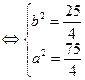 .
.
Подставляя найденные значения в уравнение (26), получим искомое уравнение гиперболы:
 или 4 y 2 – 12 x 2 = 75.
или 4 y 2 – 12 x 2 = 75.
Ответ: 4 y 2 – 12 x 2 = 75.
Задача 6. Написать разложение вектора x по базису p, q, r, если
x = (2, –1, 1)
p = (1; 1; 1), q = (0; 2;3), r = (0; 1;5).
Решение[2]
1. Пусть 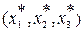 - координаты вектора x в новом базисе, тогда разложение вектора по базису p, q, r будет иметь вид:
- координаты вектора x в новом базисе, тогда разложение вектора по базису p, q, r будет иметь вид:
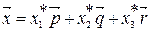 (28)
(28)
Подставим в векторное равенство (28) координаты векторов:
 .
.
Выполним линейные операции с векторами в левой части равенства:
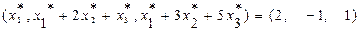 .
.
Если векторы равны, то равны и их соответствующие координаты. Приравнивая соответствующие координаты векторов, стоящих в левой и правой части равенства, получим систему линейных уравнений:
 .
.
2. Найдем решение системы, используя метод Гаусса (система может быть решена и методом Крамера). Составим расширенную матрицу системы и приедем ее к трапециевидной форме:

По виду трапециевидной матрицы заключаем, что система совместна и имеет единственное решение. Найдем значения неизвестных, решая укороченную треугольную систему:
 .
.
Подставив найденные координаты вектора в (28), получим искомое разложение вектора по базису p, q, r.
Ответ: x = 2 p – 2 q + r.
ВАРИАНТ № 1
Задание № 1
1. Вычислить линейную комбинацию матриц А и В.
Дано: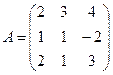 ,
, 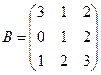 . Найти: 2А – 3В.
. Найти: 2А – 3В.
2. Вычислить произведение матриц: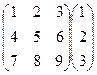 .
.
3. Найти матрицу, обратную данной: A= .
.
4. Вычислить определитель, используя подходящее разложение по строке или столбцу:
 .
.
5. Вычислить ранг матрицы 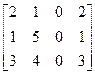 .
.
6. Решить систему линейных уравнений с помощью формул Крамера:

7. Методом Гаусса исследовать совместность и найти общее решение системы:
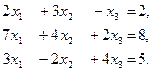 .
.
Задание № 2
5. Проверить коллинеарность векторов 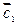 и
и 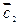 , построенных на векторах
, построенных на векторах 
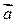 и
и 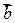 , если
, если

6. Найти косинус угла между векторами  и
и 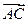 , если даны координаты точек:
, если даны координаты точек:
А (3; – 2; 1); В (2; 1; 6); С (1; 3; – 2).
7. Вычислить площадь параллелограмма, построенного на векторах 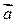 и
и 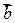 , если:
, если:
а)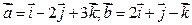 ;
;
в) 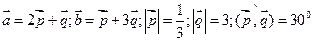 .
.
8. Составить уравнение стороны АВ треугольника, если точки
А (1; 3) и С (– 2, 4) – его вершины, а М (2, 1) –точка пересечения его высот.
9. В эллипс вписана окружность 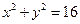 , пересекающая большую ось в фокусах, лежащих на оси OX. Составить уравнение эллипса. Сделать чертеж.
, пересекающая большую ось в фокусах, лежащих на оси OX. Составить уравнение эллипса. Сделать чертеж.
10. Написать разложение вектора 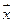 по базису
по базису 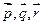 если
если 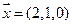 ,
,
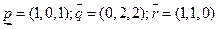 .
.
ВАРИАНТ № 2
Задание № 1
1. Вычислить линейную комбинацию матриц А и В.
Дано: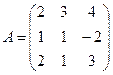 ,
, 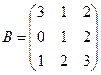 . Найти: 3А – 2В.
. Найти: 3А – 2В.
2. Вычислить произведение матриц: 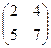
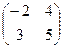 .
.
3. Найти матрицу, обратную данной: A=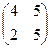 .
.
4. Вычислить определитель, используя подходящее разложение по строке или столбцу
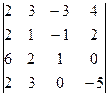 .
.
5. Вычислить ранг матрицы  .
.
6. Решить систему линейных уравнений с помощью формул Крамера:
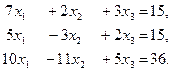
7. Методом Гаусса исследовать совместность и найти общее решение системы:
 .
.
Задание № 2
1. Проверить коллинеарность векторов 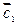 и
и 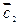 , построенных на векторах
, построенных на векторах 
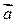 и
и 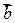 , если
, если
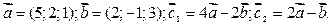
2. Найти косинус угла между векторами  и
и 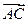 , если даны координаты точек:
, если даны координаты точек:
А (10; 2; –5); В (3; –1; 2); С (0; 5; – 2).
3. Вычислить площадь параллелограмма, построенного на векторах 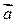 и
и 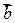 , если:
, если:
а) ;
;
в)
 .
.
4. Составить уравнение прямой, проходящей через точку С, которая
делит отрезок AB в отношении 2:1, параллельно прямой 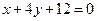 , если А (2; 1), В (12,–6).
, если А (2; 1), В (12,–6).
5. Составить уравнение окружности с центром в одной из вершин эллипса 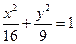 и проходящей через фокус параболы
и проходящей через фокус параболы 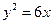 . Сделать чертеж.
. Сделать чертеж.
6. Написать разложение вектора 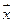 по базису
по базису 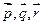 если
если 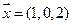 ,
,
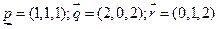 .
.
ВАРИАНТ № 3
Задание № 1
1. Вычислить линейную комбинацию матриц А и В:
Дано: ,
, 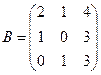 . Найти: 3А + 2В.
. Найти: 3А + 2В.
2. Вычислить произведение матриц: 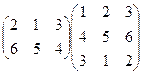 .
.
3. Найти матрицу, обратную данной: A= .
.
4. Вычислить определитель, используя подходящее разложение по строке или столбцу
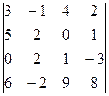 .
.
5. Вычислить ранг матрицы  .
.
6. Решить систему линейных уравнений с помощью формул Крамера:

7. Методом Гаусса исследовать совместность и найти общее решение системы:
 .
.
Задание № 2
1. Проверить коллинеарность векторов 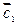 и
и 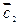 , построенных на векторах
, построенных на векторах 
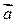 и
и 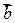 , если
, если

2. Найти косинус угла между векторами  и
и 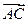 , если даны координаты точек:
, если даны координаты точек:
А (1; –3; 4); В (–3; 1; 2); С (2; 4; –5).
3. Вычислить площадь параллелограмма, построенного на векторах 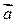 и
и 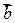 , если:
, если:
а)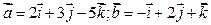 ;
;
в )
 .
.
4. В треугольнике с вершинами А (4; 1), В (–1; 5) и С (3; –1) найти уравнение стороны АС, медианы ВЕ и высоты ВD.
5. Составить уравнение гиперболы, фокусы которой расположены на оси OY симметрично относительно начала координат, зная, что расстояние между фокусами равно 12, а угол между асимптотами кривой равен 900. Сделать чертеж.
6. Написать разложение вектора 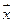 по базису
по базису 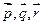 если
если 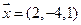 ,
,
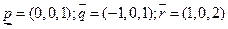 .
.
ВАРИАНТ № 4
Задание № 1
1. Вычислить линейную комбинацию матриц А и В.
Дано: ,
, 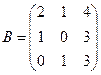 . Найти: А – 2В.
. Найти: А – 2В.
2. Вычислить произведение матриц: 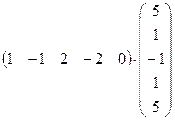 .
.
3. Найти матрицу, обратную данной: A=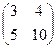 .
.
4. Вычислить определитель, используя подходящее разложение по строке или столбцу  .
.
5. Вычислить ранг матрицы 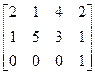 .
.
6. Решить систему линейных уравнений с помощью формул Крамера:
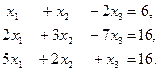
7. Методом Гаусса исследовать совместность и найти общее решение системы:
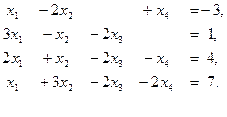 .
.
Задание № 2
1. Проверить коллинеарность векторов 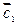 и
и 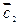 , построенных на векторах
, построенных на векторах 