Основные ФОРМУЛЫ, термины и определения

Раздел "Линейная алгебра"

1. Матрицей размера mxn называется совокупность m n выражений, расположенных в виде прямоугольной таблицы из m строк и n столбцов.

2. Квадратной матрицей порядка n называется матрица, в которой m = n, т.е. число строк равно числу столбцов.

3. Матрицей-строкой (вектор строкой) называется матрица размером, состоящая из одной строки.

4. Матрицей-столбцом (вектор строкой) называется матрица размером, состоящая из одного столбца.

5. Матрица, все элементы которой равны нулю, называется нулевой матрицей и обозначается 0 или (0)_mxn (в алгебре матриц эта матрица играет роль нуля).

6. Квадратнаяматрица, в которой отличны от нуля только элементы, стоящие на главной диагонали, называется диагональной

7. Диагональная матрица, в которой все элементы главной диагонали – единицы, называется единичной матрицей и обозначается символом E.

8.: Минором M_ij элемента a_ij определителя D порядка n называется определитель порядка (n-1), получающийся из D вычеркиванием i-ой строки и j-го столбца.

9. Алгебраическим дополнением А_ij элемента a_ij называется минор М_ij этого элемента, взятый со знаком " + " или " – " согласно формуле:

.

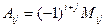10. Теорема разложения: определитель равен сумме произведений всех элементов какой-либо строки (или какого-либо столбца) на их алгебраические дополнения.

11. Обратной матрицей по отношению к квадратной матрице А порядка n называется матрица А^-1 порядка n, удовлетворяющая равенству:

.

12. Вырожденная (особенная) матрица – матрица, определитель которой равен нулю (detA = 0).

13. Система линейных уравнений – система, в которой заданы m линейных уравнений с n неизвестными и требуется найти n чисел, которые одновременно удовлетворяют каждому из m уравнений.

14. Матричная запись системы линейных уравнений (или матричное уравнение):

.

15. Матричное решение системы ( метод обратной матрицы):

.

16. Теорема Крамера.:если определитель системы n линейных уравнений с n неизвестными отличен от нуля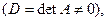то система совместнаи имеет единственное решение Х, которое определяется по формулам: ,.

17. Рангом матрицы А называется наивысший порядок отличного от нуля определителя, который можно построить из элементов данной матрицы.

18. Теорема Кронекера-Капелли (критерий совместности системы линейных уравнений): система mxn линейных уравнений совместна, если ранг матрицы системы r равен рангу её расширенной матрицы, причем, если r = n (ранг матрицы равен числу неизвестных), то система имеет единственное решение; если r < n, то система имеет бесчисленное множество решений.

19. Алгоритм Гаусса для нахождения решения системы линейных уравнений состоит в том, чтобы получить расширенную матрицу системы 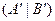трапециевидной формы.

Раздел "Аналитическая геометрия"

1. Вектором называют направленный отрезок.

2. В трехмерном пространствекаждый вектор 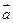может быть единственным образом представлен в виде разложения по ортам прямоугольной системы координат, т.е. в виде:

,

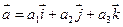где – координаты вектора.

3. Длиной или модулем вектора называют длину отрезка, изображающего вектор. Модуль вектора выражается через его координаты формулой .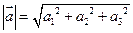

3. Если вектор задан координатами его конца (точка) и начала (точка), то координаты вектора определяются выражением

.

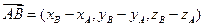4. Коллинеарными называются векторы, лежащие на одной прямой или на параллельных прямых.

5. Векторы называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.

6. Условие коллинеарности векторов в координатной форме:

.

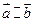
7. Скалярным произведением векторов 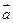и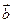называется число, равное произведению модулей векторов на косинус угла между ними:

.

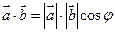8. Скалярное произведение векторов равно сумме произведений соответствующих координат векторов (скалярное произведение векторов в координатной форме):

.

9. Косинус угла между векторами определяется с помощью скалярного произведения:

.=.

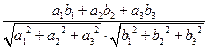10. Векторным произведением векторов 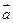и 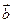называется вектор 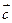, модуль которого равен произведению модулей векторов 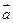и 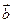на синус угла между ними, а направление вектора 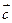перпендикулярно векторам 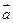и 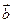, причем векторы 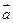,,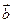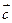образуют правую тройку векторов.

11. Модуль векторного произведения 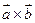равен площади параллелограмма, построенного на векторах 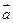и : .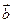

12. Векторное произведение 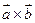в координатной форме может быть записано с помощью определителя:

.

13. Смешаннымпроизведением векторов 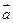,,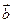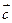называется число, равное скалярному произведению вектора 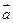на векторное произведение .

14.. Общее уравнение прямой:

.

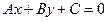15. Уравнение прямой с угловым коэффициентом:

,

где k = tg – угловой коэффициент прямой, – угол, образованный прямой с осью Оx; b – отрезок, отсекаемый прямой на оси ординат.

16. Уравнение прямой, проходящей через заданную точку в данном направлении:

,

где k– угловой коэффициент прямой, – некоторая точка, принадлежащая прямой.

17. Уравнение прямой в отрезках:

,

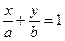где a и b –отрезки, отсекаемые прямой на осях координат.

18. Уравнение прямой, проходящей через две заданные точк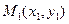и и :

.

19. Уравнение прямой, проходящей через данную точку параллельно данному вектору

.

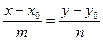20. Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору :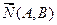

.

21. Условие параллельности прямых 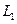и 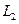, заданных общим уравнением

,

22. Условие перпендикулярности прямых, заданных общими уравнениями

,

т.е. условием перпендикулярности прямых является равенство нулю суммы произведений коэффициентов при переменных.

23. Условие параллельности прямых, заданных уравнениями с угловым коэффициентом:

,

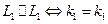т. е. для того чтобы две прямые были параллельны, необходимо и достаточно, чтобы были равны их угловые коэффициенты.

24. Условие перпендикулярности прямых, заданных уравнениям с угловым коэффициентом:

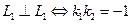, или

т.е. для того чтобы две прямые были перпендикулярны, необходимо и достаточно, чтобы произведение их угловых коэффициентов было равно минус единице.

25. Эллипсом называется кривая второго порядка, каноническое уравнение которой имеет вид

,

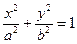где параметры a и b – полуоси эллипса.

26. Уравнение окружности с центром в точке 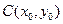и радиусом, равным R:

.

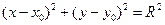27. Гиперболой называется кривая второго порядка, каноническое уравнение которой имеет вид

,

где параметр a называется вещественной полуосью, b – мнимой полуосью.

28. Параболой называется кривая второго порядка, каноническое уравнение которой имеет вид

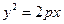, или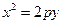

где р – параметр параболы.

ЛИТЕРАТУРА

1. Н.В.Кожусь. Линейная алгебра. Учебное пособие. СПб: РИО СПб филиала РТА, 2006. ­ 44с.

2. Н.В.Кожусь. Математика. Курс лекций. ­ СПб: РИО СПб филиалак РТА, 2008. ­ 170 с.

3. Высшая математика для экономистов. Учебник для вузов./Под ред. Проф. Н.Ш. Кремера. – М.: Банки и биржи, ЮНИТИ, 1998. – 491 с.

4. В.С.Шипачев. Высшая математика. – М.: Высшая школа. 1985.

5. В.С.Шипачев. Задачник по высшей математике: учебное пособие для вузов. – 2-ое изд., М.: Высшая школа, 2001. – 304 с.

6. М.С.Красс. Математика для экономических специальностей. - М.: Инфра. – М. 1998.

7. Сборник задач по математике для ВУЗов: Линейная алгебра и основы математического анализа. / Под ред. А.В. Ефимова и Б.П. Демидовича. – М.: Наука, 1986.

Дополнительная литература

1. Общий курс высшей математики для экономистов: Учебник. /Под ред. В.И. Ермакова. - М.:ИНФРА-М, 2001.- 656 с.

2. Ф.И.Карпелевич, Л.Е. Садовский. Элементы линейной алгебры и линейного программирования. - М.: Наука, 1967. - 274с.

3. А.Г.Курош. Курс высшей алгебры. - М.: Наука, 1971. - 431с.

4. Х.Д.Икрамов. Задачник по линейной алгебре. – М.: Наука, 1975.

5. Д.К. Фадеев, И.С. Соминский. Сборник задач по высшей алгебре. - М.: Наука, 1977.-287с.

6. Н.В.Ефимов. Краткий курс аналитической геометрии. – М.: Наука, 1975.

7. В.А.Ильин, Э.Г. Позняк. Линейная алгебра. – М.: Наука, 1983.

8. Д.В.Беклемишев. Курс аналитической геометрии и линейной алгебры. - М.: Наука, 1980.

9. В.А.Ильин, Э.Г.Позняк. Аналитическая геометрия. - М.: Наука, 1971.

10. Д.В.Клетеник. Сборник задач по аналитической геометрии. М.: Наука, 1986.

ПРИЛОЖЕНИЕ

Образец оформления титульного листа контрольной работы

Государственное образовательное учреждение высшего профессионального образования «Российская таможенная академия» Санкт-Петербургский имени В.Б.Бобкова филиал Российской таможенной академии _______________________________________________________________ Кафедра информатики и информационных таможенных технологий     КОНТРОЛЬНАЯ РАБОТА по дисциплине «Математика» Вариант № 1
	Выполнил: слушатель 1курса номер группы заочного отделения экономического факультета И.О.Фамилия   Проверил: И.О.Фамилия Ученая степень, должность
Санкт-Петербург

[1] Данный пункт решения не является обязательным.

[2] Данная задача может быть решена также с использованием матрицы перехода.

Дата добавления: 2014-10-23