Тема: «Разработка формальной грамматики Хомского»

Расчетно-графическая работа №2

1 Теоретическая часть

1.1 Формальная грамматика

Грамматика языка – это набор средств для его описания. Различают порождающие и распознающие грамматики, в зависимости от того, какая задача ставится: строить новые цепочки языка или определять принадлежит или нет некоторая цепочка языку.

Формальной порождающей грамматикой G называется следующая совокупность четырех объектов:

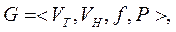где V_T - терминальный алфавит (словарь); буквы этого алфавита называются терминальными символами; из них строятся цепочки порождаемые грамматикой; V_H - нетерминальный, вспомогательный алфавит (словарь); буквы этого алфавита используются при построении цепочек; они могут входить в промежуточные цепочки, но не должны входить в результат порождения; f - начальный символ грамматики f Î V_H; P - множество правил вывода или порождающих правил вида a → b, где a и b - цепочки, построенные из букв алфавита V_T и V_H, который называют полным алфавитом (словарем) грамматики G.

Множество конечных цепочек терминального алфавита V_T грамматики G, выводимых из начального символа f, называется языком, порождаемым грамматикой G и обозначается L (G):

1.2 Пример построения грамматики

Примером языка может являться множество различных корректных формул, включающих в себя натуральные числа, скобки и знаки арифметических действий. Алфавитом в этом случае будет множество Σ = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, +, -, *, /, (,) }. Например, строка (2+3)*(5+7) будет словом такого языка, а строка +2(3-1( не будет (хотя она и состоит из допустимых символов, но записана с очевидными ошибками). Как можно описать этот язык? Мы знаем, что числа состоят из цифр и могут объединяться с помощью знаков арифметических действий в формулы (например, формулой будет цепочка 2+3). Формулы можно заключать в скобки, а также складывать, вычитать, умножать и делить — то есть объединять друг с другом (и с числами) в более сложные формулы. Например, (2+3)*(5+7) — это сложная формула, состоящая из двух более простых, ее можно символически записать следующим образом: ФОРМУЛА ЗНАК ФОРМУЛА. Заметим, что вместо слов ФОРМУЛА можно подставить любую корректную формулу, а вместо слова ЗНАК — знак любого арифметического действия, и эта строка останется правильной формулой.

Идея теории порождающих формальных грамматик, разработанной Н. Хомским, состоит в том, чтобы описывать язык через правила подстановок, которые позволяют строить слова языка из «кирпичиков», описываемых с помощью других «кирпичиков». Правила языка при этом можно записывать, просто указывая, какие цепочки «кирпичиков» можно подставлять вместо других «кирпичиков». Например, разобранное выше правило построения сложных формул из простых можно записать следующим образом (такая запись называется правилом вывода )

1. ФОРМУЛА → ФОРМУЛА ЗНАК ФОРМУЛА

Правило нужно читать так: «вместо слова ФОРМУЛА можно подставить цепочку ФОРМУЛА ЗНАК ФОРМУЛА». При этом вместо «кирпичика» ЗНАК можно подставлять один из четырех символов алфавита Σ: (+, -, *, /). Это можно записать с помощью следующих четырех правил.

2. ЗНАК→ +

3. ЗНАК→ -

4. ЗНАК→ *

5. ЗНАК→ /

Такая запись обычно сокращается до следующей (символ "|" не принадлежит Σ).

6. ЗНАК→ + | - | * | /

«Кирпичики», обозначаемые нами большими буквами (например, ЗНАК), не являются символами рабочего алфавита Σ (хотя и могут быть на них заменены в процессе подстановок). Они называются «нетерминалами» (или «нетерминальными символами»), в отличие от букв алфавита Σ, называющихся терминалами. Смысл этих названий состоит в том, что нетерминал может быть заменен на цепочку других символов (как в случае с нетерминалом ФОРМУЛА), в то время как терминал уже ни на что заменен быть не может и является своеобразным «пунктном назначения» наших замен (от англ. terminal — конечный пункт). Чтобы получить слово языка, мы должны все нетерминалы в конечном итоге заменить на терминалы, а для этого в описание языка должны входить соответствующие правила.

В рассмотренном примере для определения нетерминала ЧИСЛО можно ввести такие правила

7. ЧИСЛО→ ЦИФРА | ЧИСЛО ЦИФРА

8. ЦИФРА → 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9

Иными словами, если к числу приписать справа еще одну цифру, то получится снова число. Одно число — это также корректная формула, что записывается следующим образом:

9. ФОРМУЛА→ ЧИСЛО

Для полного описания грамматики нам требуется также разрешить заключать формулы в скобки. Это делается с помощью правила

10. ФОРМУЛА→ (ФОРМУЛА)

Надо отметить, что нетерминал ФОРМУЛА в нашем случае является выделенным — он задает правильные формулы, то есть слова нашего языка, в то время как, например, нетерминал ЗНАК не задает слово языка. В таком случае говорят, что нетерминал ФОРМУЛА является начальным.

Итак, чтобы задать формальную грамматику, требуется задать алфавиты терминалов и нетерминалов, набор правил вывода, а также выделить в множестве нетерминалов начальный. Тогда словами языка, заданного грамматикой, являются все слова, состоящие только из терминалов, и при этом получаемые из начального нетерминала по правилам вывода.

Выведем формулу (12+5) с помощью перечисленных правил вывода:

ФОРМУЛА 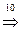(ФОРМУЛА) 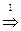(ФОРМУЛА ЗНАК ФОРМУЛА) (ФОРМУЛА + ФОРМУЛА) 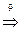(ФОРМУЛА + ЧИСЛО) 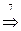(ФОРМУЛА + ЦИФРА) 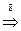(ФОРМУЛА + 5) 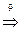(ЧИСЛО + 5) 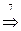(ЧИСЛО ЦИФРА + 5) 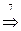(ЦИФРА ЦИФРА + 5) 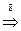(1 ЦИФРА+5) 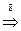(12+5)

1.3 Представление грамматики в виде графа

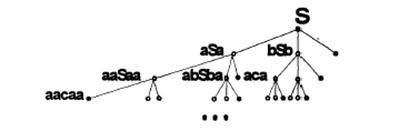
Граф грамматики в качестве вершин содержит цепочки, выводимые из начального символа. Ниже на рисунке дано представление грамматики 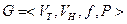, где 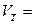{ a,b,c }, 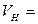{S}, 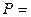{S→ aSa | bSb | c }.

1.5 Классификация формальных грамматик

Множество формальных грамматик можно разложить на классы в зависимости от ограничений, накладываемых на продукции. Такие ограничения формируют особые свойства грамматик и особые методы анализа и синтеза цепочек символов. Общепринятой классификацией грамматик и порождаемых ими языков является иерархия грамматик Хомского, содержащая четыре типа грамматик.

Грамматика типа 0 - грамматика произвольного типа без каких-либо ограничений на цепочки символов. Продукции этой грамматики имеют вид:

a::= b.

В обеих частях продукции могут быть в произвольном порядке и любом количестве терминальные и нетерминальные символы, т.е. a, bÎV*, где верхним левым индексом «*» обозначено множество с пустым символом e, а знак "::=" означает: "...присвоить значение...". Такой тип грамматики порождает множество перечислимых языков, для которых существует перечисляющий алгоритм. Такой алгоритм может быть реализован на машине Тьюринга, являющейся классической моделью рекурсивной функции. Поэтому такие языки называют также рекурсивно-перечислимыми. Однако такой тип грамматики не нашел применения в языках программирования.

Пример 1. Пусть дана грамматика G₁ = < V_T; V_H; P; J >, где

V_T = { a; b }; V_H = { A;B;C;J };

P = { р₁ : J::= AbBb; р₂ : J::= AbJBb; р₃ : Ab::= Bba;

р₄ : Bb::= Cba; р₅: Cb::= ba }.

Какие цепочки терминальных символов формирует грамматика?

Рассмотрим левосторонний вывод:

J =>AbBb =>BbaBb =>CbaaBb =>baaaBb =>baaaCba = (ba³)(ba²);

J =>AbJBb => BbaJBb => CbaaJBb => baaaJBb =>baaaAbBbBb => baaaBbaBbBb => baaaCbaaBbBb => baaabaaaBbBb => baaabaaaCbaBb =>

baaabaaabaaBb => baaabaaabaaCba => baaabaaabaabaa = (ba³)²(ba²)²;

J =>AbJBb => BbaJBb => CbaaJBb => baaaJBb => baaaAbJBb => baaaBbaJBb =>...=> baaabaaabaaabaabaabaa = (ba³)³(ba²)³; и т.д.

Грамматика G₁ формирует множество цепочек, используя процедуру итерации:

L(G₁) = { (ba³)ⁱ (ba²)ⁱ | i = 1;2;3;... }.

Пример 2. Пусть дана грамматика G₂ = < V_T; V_H; P; J >, где

V_T = { a; b }; V_H = { A;J };

P = { р₁ : J::= JAa | b; р₂ : aA::= Aa; р₃ : bA::= ab }

Какие цепочки терминальных символов формирует грамматика?

Используем также левосторонний вывод терминальных цепочек:

J => b;

J => JAa => bAa => aba;

J => JAa => JAaAa => bAaAa => abaAa => abAaa => aabaa = a²ba²;

J => JAa => JAaAa =>JAaAaAa =>... => aaabaaa = a³ba³; и т.д.

Грамматика G₂ формирует множество цепочек, также используя процедуру итерации:

L(G₂) = { aⁱbaⁱ | i = 0;1;2;3;... }.

Грамматика типа 1 - это контекстно-зависимая грамматика или грамматика непосредственных составляющих (НС-грамматика). Второе название грамматики объясняется тем, что любую цепочку можно разложить на синтаксические составляющие (члены предложения естественного языка) и выполнить разбор каждой синтаксической переменной (части речи естественного языка) в составе синтаксической составляющей. В естественных языках для этого проводят грамматической разбор структуры предложения. В языках программирования - грамматический разбор структуры программы, что всегда необходимо при трансляции исходной программы на язык вычислительной машины.

Продукции этой грамматики имеют вид:

w₁Aw₂::= w₁bw₂,

где AÎV_H;

w₁, w₂, bÎV*,

w₁ - левый контекст,

w₂ - правый контекст.

Каждый шаг вывода состоит в замене одного вхождения нетерминального символа вхождением цепочки терминальных и/или нетерминальных символов. Эта замена обусловлена наличием левого и правого контекстов.

Для НС-грамматики существенным является исполнение условия:

|w₁Aw₂| £ |w₁bw₂|,

где |...| означает длину цепочки символов, заключенных между вертикальными линиями.

Это требует исполнения в каждом правиле второго условия:

b ¹ e.

Грамматики, в которых все правила обладают этими свойствами называют неукорачивающими.

Множество языков НС-грамматики является собственным подмножеством языков грамматики типа 0.

Для НС-грамматики возможны случаи:

1) w₁A::= w₁b, когда w₂ = e;

2) Aw₂::= bw₂, когда w₁ = e.

Для НС-грамматик также допустим лево- и правосторонний вывод, когда продукции грамматики применяются к самому левому или самому правому нетерминальному символу анализируемой цепочки.

Пример 3. Пусть дана грамматика G₃ = < V_T; V_H; P; J >, где

V_T = { a; b; c}; V_H = {B; C; J };

P = { р₁ : J::= aJBC | aBC; р₂ : CB::= DB;

р₃: DB::= DC; р₄: DC;;= BC; р₁₅: aB::= ab;

р₆ : bB::= bb; р₇ : bC::= bc; р₈ : cC::= cc }.

Какие цепочки терминальных символов формирует грамматика?

В каждом правиле есть либо левый, либо правый контексты.

Используем также левосторонний вывод терминальных цепочек:

J => aBC => abC => abc;

J => aJBC => aaBCBC => aabCBC =aabDBC => aabDCC => aabBCC => aabbCC => aabbcC => aabbcc = a²b²c²;

J => aJBC => aaJBCBC =>... => aaabbbccc = a³b³c³ и т.д.

Грамматика G₃ формирует цепочки терминальных символов, используя операцию итерации:

L(G₃) = { aⁱbⁱcⁱ | i = 1;2;3;... }.

Грамматика типа 2 - это контекстно-свободная грамматика (КС-грамматика). Правила этой грамматики не зависят от контекста, т.е. в левой части каждого правила находится только один нетерминальный символ, а в правой части цепочка терминальных и/или нетерминальных символов.

Продукции этой грамматики имеют вид:

A::= b,

где b Î V*.

Каждый шаг вывода связан с заменой в цепочке одного нетерминального символа на цепочку терминальных и/или нетерминальных символов.

Множество КС-языков при выполнении условий w₁ = e, w₂ = e и b ¹ e является подмножеством НС-языков.

КС-грамматики наиболее эффективно описывают состав и структуру формального языка. Поэтому они нашли применение в большинстве языков программирования. Для унификации языков программирования были разработаны метаязыковые средства описания синтаксических конструкций. Особое место среди этих средств занимают формулы Бэкуса-Наура (БНФ).

Для КС-грамматик также удобен фиксированный способ вывода (лево- или правосторонний).

Пример 4. Пусть дана грамматика G₄ = < V_T; V_N; P; J >,

где V_T = { буква; цифра}; V_H = {A; B; J };

P = { р₁ : J::= JA | JB | A;

р₂ : A::= буква;

р₃ : B::= цифра }.

Какие цепочки терминальных символов формирует грамматики?

Для удобства доказательства сохраним левосторонний вывод:

J => A => буква;

J => JA => AA => буква буква;

J => JB => AB => буква цифра;

J => JA => JAA => AAA =>... => буква буква буква;

J => JA => JBA => ABA =>... => буква цифра буква;

J => JB => JAB => AAB =>...=> буква буква цифра;

J => JB => JBB => ABB =>...=> буква цифра цифра и т.д.

Грамматика G₄ формирует следующие цепочки терминальных символов:

L(G₄) = { буква { буква | цифра } }.

Такова грамматика для формирования идентификаторов большинства языков программирования.

Грамматика типа 3 (регулярная) - это линейная грамматика, правила которой содержат в правой части не более одного нетерминального символа.

Продукции этой грамматики имеют вид:

A::= w₁Bw₂ или A::= w,

где w₁, w₂, wÎV*\V_N.

Продукция линейной грамматики называется праволинейной (леволинейной), если единственный нетерминальный символ в правой части продукции всегда находится крайним справа (слева).

Например, А::= w₁B - праволинейная продукция,

A::= Bw₂ - леволинейная продукция.

Если все продукции грамматики праволинейные или леволинейные, то грамматика также называется праволинейной или леволинейной. Каждой праволинейной грамматике соответствует эквивалентная ей леволинейная грамматика. В зависимости от типа грамматики различают праволинейные и леволинейные языки.

Языки линейной грамматики представляют собственное подмножество множества КС-языков.

Пример 5. Пусть дана грамматика G₅ = < V_T; V_H; P; J >

где V_T = {a; b; c }; V_H = { A; B; J; };

P = { р₁ : J::= Bb; р₂ : A::= Aa | a; р₃ : B::= Bb | Aac | ac }.

Какие цепочки терминальных символов формирует грамматика?

Можно отметить, что все правила этой грамматики -леволинейные.

Проведем левосторонний вывод терминальных цепочек:

J Þ Bb Þ acb

ß Þ Aacb Þ aacb

acbb Ü Bbb ß

ß ß Þ Þ Þ

ß ß

aacbb Ü Aacbb Üß Aaacb Þ aaacb

ß ß ß

aaacbb Ü Aaacb ß...

Bbbb Þ acbbb

ß

...

Грамматика G₅ формирует цепочки вида:

L(G₅) = { aⁱcb^j | i,j = 1;2;3;... }.

2 Примеры решения задач

Пример 1. Приведите примеры не менее чем пяти языков в алфавите:

Σ={a,b,c,d,e}

Пример 2. Построить праволинейную грамматику для языка, состоящего из 1 и 0 с четным числом нулей и единиц.

Пример 3. Построить КС-грамматику, порождающую правильно расставленные скобки

Пример 4. Даны грамматики G1 = ({0,1}, {A,S}, P1, S) и G2 = ({0,1}, {S}, P2, S).

P1: S→0A1, 0A→00A1, A→e и P2: S→0S1 | 01. Определить языки грамматик и их типы.

Пример 5. Построить грамматику, порождающую язык L = { aⁿbⁿcⁿ | n >0}. Получить вывод терминальной цепочки aaabbbccc.

3 Задание

Для выбранной в соответствии с вариантом задания задачи:

1) Разработать формальную грамматику Хомского G, порождающую цепочки языка L(G).

2) Построить вывод заданной в варианте задания цепочки.

3) Представить грамматику в виде графа.

4) Определить класс, к которому принадлежит грамматика.

5) Сделать выводы.

4 Содержание отчета

1) Определение понятия «Формальная грамматика Хомского».

2) Определение алфавита терминальных символов.

3) Определение алфавита нетерминальных символов.

4) Определение начального символа.

5) Определение правил вывода.

6) Вывод заданной цепочки языка.

7) Разработка графа грамматики.

8) Определение класса грамматики.

9) Анализ результатов и выводы.

5 Варианты задания

Ниже даны варианты задания, в каждом из которых в качестве способа описания формального языка выбран алгебраический способ. Помимо алгебраического описания языка вариант задания включает цепочку, для которой должен быть построен вывод в грамматике.

1.

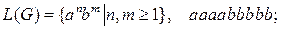
2.

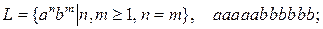
3.

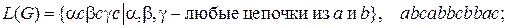
4.

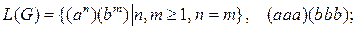
5.

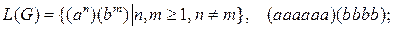
6.

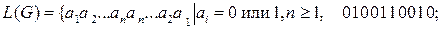
7.

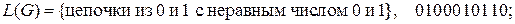
8.

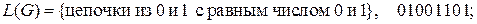
9.

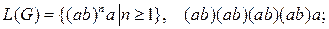
10.

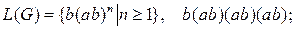
11.

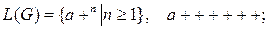
12.

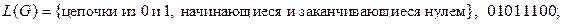
13.

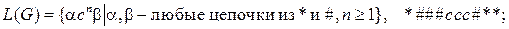
14.

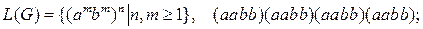
15.

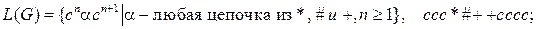
16.

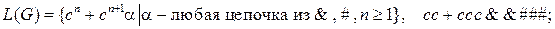
17. L(G) = {1³ⁿ⁺² 0ⁿ | n≥0}, 1111111100;

18. L(G) = {0ⁿ 1^m | n>m и n,m >0 }, 00000000011111;

19. L(G) = { aⁿb^3mc^ma²ⁿ | n>1 и m>1 }, aabbbbbbccaaaa.

6 Список литературы

1) Волкова И.А., Руденко Т.В. Формальные грамматики и языки. Элементы теории трансляции. / Учебное пособие для студентов II курса. Издание второе. - М: ВМиК МГУ, 1999.

2) Пономарев В.Ф. Формальные языки и грамматики. / Учебное пособие. - Калининград: КГТУ, 1998.

Дата добавления: 2014-10-31