
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Коэффициент трения качения
|
|
|
|
Как видно из формулы (4.10), сопротивление качения характеризуется коэффициент трения качения k, который имеет разновидность длины. Значение k определяют опытным путём: для пары сталь-сталь k=0.003…0.0005 см, для пары закалённая сталь - закалённая сталь k=0.001 см.
Потери на трение качения значительно меньше, чем на трение скольжения. Поэтому во многих механизмах, а особенно в приборах, где силы трения являются главными сопротивлениями, конструкции выполняются так, чтобы трение скольжения заменить трение качения.
Глава 5. СИНТЕЗ ЗУБЧАТЫХ МЕХАНИЗМОВ
5.1. Основная теорема и основной закон зацепления 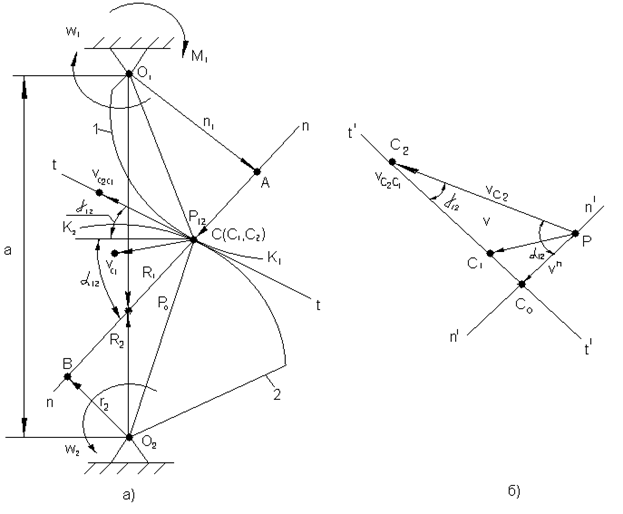
Рис. 5.1. К определению форм профиля двух взаимоогибаемых кривых: а - схема механизма с высшей парой; б – план скоростей.
Пусть передача вращения между двумя осями 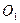 и
и  (рис. 5.1,а) с угловыми скоростями
(рис. 5.1,а) с угловыми скоростями 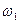 и
и 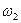 осуществляется посредством двух взаимоогибаемых кривых
осуществляется посредством двух взаимоогибаемых кривых 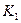 и
и 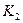 , принадлежащих звеньям 1 и 2. Проведём в точке соприкосновения C кривых
, принадлежащих звеньям 1 и 2. Проведём в точке соприкосновения C кривых 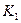 и
и 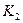 нормаль n – n и касательную t – t к этим кривым.
нормаль n – n и касательную t – t к этим кривым.
Скорости 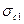 и
и 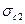 точек
точек 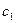 и
и 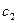 принадлежащим звеньям 1 и 2, связаны условием
принадлежащим звеньям 1 и 2, связаны условием
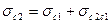
План скоростей механизма, построенный по этому уравнению, показан на рис. 5.1,б
Из точек 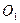 и
и  (рис.5.1,а) опускаем на нормаль n-n перпендикуляры
(рис.5.1,а) опускаем на нормаль n-n перпендикуляры 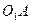 и
и 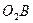 , а из полюса плана скоростей (рис. 5.1,б)- перпендикуляр
, а из полюса плана скоростей (рис. 5.1,б)- перпендикуляр 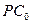 на направлении
на направлении  .
.
Отрезок (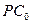 ) представляет собой нормальную составляющую
) представляет собой нормальную составляющую  векторов скоростей
векторов скоростей 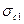 и
и 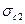 .
.
Из подобия 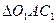 и
и 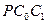 и
и 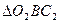 и
и 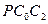 имеем
имеем
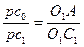 и
и 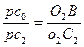 (5.1)
(5.1)
Отрезки (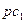 ),(
),(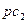 ), (
), (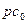 ) представляют собой соответственно скорости
) представляют собой соответственно скорости 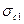 ,
, 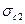 и
и  . Тогда соотношения (9.1) могут быть представлены так:
. Тогда соотношения (9.1) могут быть представлены так:
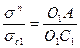 и
и 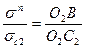 ,
,
или
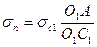 и
и 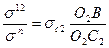 .
.
Заменяя 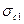 и
и 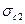 их значениями, равными
их значениями, равными 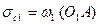 и
и 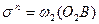 , откуда
, откуда

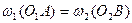
 (5.2)
(5.2)
Следовательно, передаточная функция  равна
равна
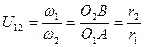 (5.3)
(5.3)
Продолжим нормаль n-n до пересечения в точке 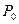 c отрезком
c отрезком 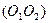 . Тогда из подобия
. Тогда из подобия 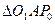 и
и 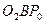 имеем
имеем
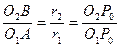 ,
,
и формула (5.3) принимает окончательный вид:
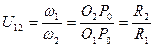 (5.4)
(5.4)
|
|
|
|
|
Дата добавления: 2014-10-31; Просмотров: 438; Нарушение авторских прав?; Мы поможем в написании вашей работы!