Взнос на амортизацию единицы

Данная функция используется для определения величины одного аннуитетного платежа при известной текущей стоимости серии таких платежей. (На практике это нужно для расчета величин платежей по ипотечным кредитам, погашаемым равными выплатами). Эта функция является обратной функции текущей стоимости аннуитета. Величина искомого платежа обозначается как РМТ. Если известна основная сумма кредита (текущая стоимость серии платежей на момент “0”), следует использовать обратную формулу 1/a(n,i) для расчета величины одного платежа PMT- денежной суммы, которую необходимо вносить в конце каждого периода времени для того, чтобы выплатить весь кредит с учетом процентов. Кредит будет погашаться или “амортизироваться” равными платежами. Величина РМТ=1/ a(n,i) называется взносом на амортизацию единицы.

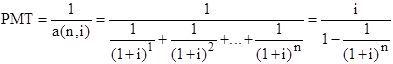
Текущую стоимость PV=1 можно рассматривать как сумму, “превращающуюся” в серию платежей, каждый из которых равен 1/ a(n,i). Предположим, что на счет в банке положена сумма, равная 1, при условии накопления i% за каждый период. В конце периода 1 сумма равная 1/ a(n,i), может быть снята со счета, а на остаток на счете будет начисляться процент. Аналогично, в конце периода 2 со счета может быть снята сумма, равная 1/ a(n,i), и так далее, включая период n. В конце периода n, когда будет произведен последний платеж, равный 1/ a(n,i), остаток на банковском счете будет равен 0.

В таблицах данный фактор показан в колонке 6.

Таблицы амортизации

Рассмотрим кредит, основная сумма которого равна PV, и который должен быть погашен равными платежами PMT=PV/ a(n,i) за периоды 1, 2,..., n. Каждый платеж, включает выплату как процентов, так основной суммы займа. Процентные выплаты будут направляться на обслуживание долга; они не уменьшают остаток основной суммы кредита. Остальная часть платежа пойдет на выплату (сокращение) основной суммы долга. Какую часть платежа составляет выплата процента, и какую часть - выплата основной суммы долга?

Наиболее распространенный способ определения структуры платежа по кредиту заключается в том, что из него вычитается процент, подлежащий выплате в данный период, а оставшаяся часть платежа считается равной выплате основной суммы кредита.

Предположим, что Bal(k) - это остаток по кредиту после того, как в конце периода k был произведен очередной платеж. Начальная сумма кредита Bal(0)=PV. В конце первого периода должен быть выплачен процент по кредиту в сумме, равной i*PV=i Bal(0). Если из периодичного платежа PMT вычесть процентные выплаты iBal(0), то получим часть платежа, идущую на погашение основной суммы долга. Новый остаток по кредиту на конец первого периода (начало второго периода) будет равен первоначальному остатку за вычетом выплат основной суммы долга, т. е. Bal(1)= Bal(0)-(PMT-i Bal(0)). В целом, процент, который должен быть выплачен по кредиту в конце периода k, равен i Bal(k-1), поэтому за период k основной долг уменьшится на следующую величину:

PR(k)=PMT-i Bal(k-1)

Где PR (k) – выплата основной суммы долга за период k

Новый остаток в конце периода k будет равен:

Bal(k)= Bal(k-1)-PR(k)= Bal(k-1)-(PMT-i Bal(k-1))

Последний платеж в конце периода n сведет остаток долга к нулю, т. е. PR(n)= Bal(n-1) и Bal(n)=0.

Расчет структуры периодического платежа обычно проводится в следующей форме:

ТАБЛИЦА АМОРТИЗАЦИИ/ГРАФИК ПОГАШЕНИЯ КРЕДИТА

Период	Остаток на начало периода	Платеж	Выплаты процента	Выплаты основной суммы долга	Остаток на конец периода
	PV	PMT	iPV	PMT-iPV	Bal(1)
	Bal(1)	PMT	i Bal(1)	PMT-i Bal(1)	Bal(2)
...	...	...	...	...	...
n-1	Bal(n-2)	PMT	i Bal(n-2)	PMT-i Bal(n-2)	Bal(n-1)
n	Bal(n-1)	PMT	i Bal(n-2)	PMT-i Bal(n-1)

Дата добавления: 2014-10-31