Вопросы для контроля

7. Какими должны быть ежегодные платежи по ипотеке в 100.000 долл. при 12% годовых? Выплата производится раз в год, срок погашения кредита 25 лет.

Решение:

100.000*0,1275=12750

8. Рассчитать ежемесячные платежи в погашение кредита, предоставленного в сумме 2.500.000 тенге. на два года при номинальной годовой ставке 96%.

Решение:

n=2*12=24

i=96:12=8

0,094978*2500=237.445

9. Каким должен быть ежегодный платеж в погашение 1000-долларового кредита, предоставленного под 10% годовых на четыре года? Составьте график амортизации.

Решение:

1000*0,3154708=315,4708

Период	Остаток на начало периода	Платеж	Выплаты процента	Выплаты основной суммы долга	Остаток на конец периода
1.		315,4708		215,4708	784,5292
2.	784,5292	315,4708	78,45,92	237,0179	547,5113
3.	547,5113	315,4708	54,75113	260,7197	286,7916
4.	286,7916	315,4708	28,67916	286,7916

2.5. Накопление единицы на период (будущая стоимость аннуитета)

Предположим, что вместо рассмотрения текущей стоимости серии равновеликих платежей, нужно знать будущую стоимость, которая должна быть получена в конце периода n за счет внесения равных платежей через промежутки времени t=1, 2,..., n. Данная практика депонирования равных взносов на протяжении серии временных периодов и накопления их до определенной будущей суммы, называется формированием “фонда возмещения”. Каждая денежная сумма, положенная на соответствующий счет, будет в течение n периодов накапливаться в будущую стоимость, а сумма этих будущих стоимостей и будет общей накопленной стоимостью фонда возмещения. Если каждый платеж в фонд равен единице, то общая будущая сумма называется накоплением единицы за период и обозначается s(n,i).

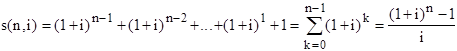
Поскольку формула накопления единицы за период просто обозначает текущую стоимость единичного аннуитета как будущую стоимость в конце периода n, то мы получаем:

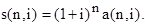
В таблице данный фактор показан в колонке 2.

Рисунок иллюстрирует накопление искомой будущей стоимости аннуитета s (n,i) в момент времени n, складывающейся из отдельных аннуитетных платежей, каждый из которых равен 1.

Дата добавления: 2014-10-31