Лабораторная работа №5. Решение задач линейной алгебры

Решение задач линейной алгебры

Цель работы

Использование возможностей MathCAD при решении задач линейной алгебры..

Задачи:

- умение применять различные способы при вычислении в Mathcad;

Порядок выполнения

Задание №1:

Для матрицы А (2;3) найти:

1. транспонированную;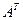

2. обратную ;

3. Вычислить: С=А*В, где В (3;2)

4. Вычислить определитель матрицы С.

1. Необходимо задать матрицу А выполнив: Добавить – Матрицу, в появившимся окне указать параметры исходной матрицы (рис. 19).

Рис 19. Вставка матрицы

,

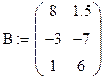
2. Для определения транспонированной матрицы выбрать кнопку , обратной 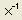на панели инструментов «Матрица» (рис.20).

При вычислении обратной матрицы в данном примере будет ошибка, т.к. матрица не является квадратной, можно найти обратную матрицу для квадратной и сравнить результат с вычисленным значением самостоятельно.

Рис 20. Матрица

3. Затем ввести матрицу В, и вычислить матрицу С.

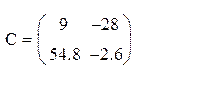
4. Определитель для матрицы С можно вычислить с помощью команды: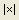

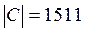
Самостоятельно:

Даны матрицы , найти:

1. транспонированные:, ;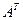

2. обратные: , ;

3. С=А²*В+ 3*В^-1

4. Вычислить определитель матриц А^T, В^-1 , С.

Задание №2:

Решить уравнения и выполнить проверку.

Матричное уравнение – это уравнение вида , неизвестную матрицу можно вычислить так: 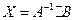или 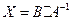. Матричное уравнение имеет единственной решение, если А и В – квадратные матрицы n – порядка и определитель матрицы А не равен нулю.

а). Вычислить неизвестную матрицу Х:

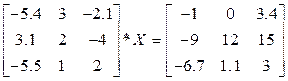
Решение на рис.21:

б). Вычислить неизвестную матрицу Х:

,

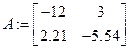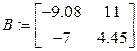
Решение на рис.22:

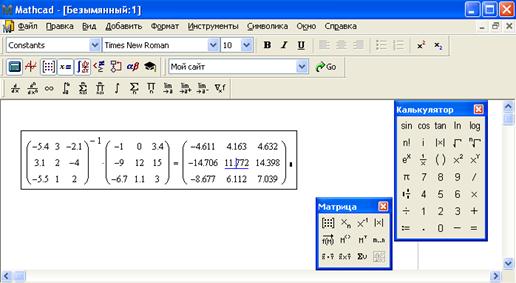
Рис 21. Решение матрицы

Рис 22. Проверка решения уравнения

Самостоятельно:

1. Вычислить неизвестную матрицу Х, выполнить проверку:

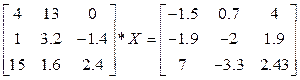
2. Вычислить неизвестную матрицу Х выполнить проверку:

,

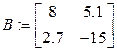
3. Вычислить неизвестную матрицу Х выполнить проверку:

,

Задание №3:

Решить систему уравнений:

а) методом Крамера

б) методом обратной матрицы

в) методом Гаусса

а) Для решения системы уравнений по правилу Крамера, необходимо выполнить следующую последовательность действий:

1. Представить систему в матричном виде, т.е. сформировать матрицу системы А и вектор правых частей.

2. Вычислить главный определитель.

3. Сформировать вспомогательные матрицы для вычисления определителей: .

4. Найти решение системы уравнений по формулам: , 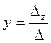(на примере системы уравнений с тремя неизвестными x,y,z).

Система уравнений:

Решение на рис. 23.

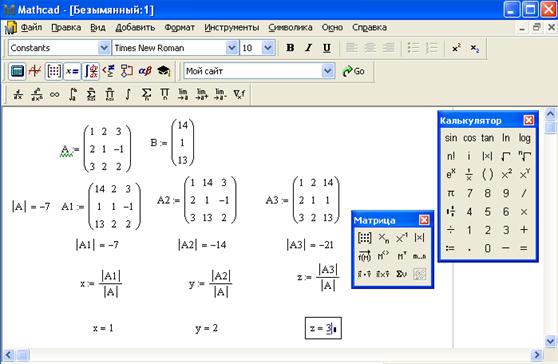
Рис 23. Решение системы уравнений

б). Для решения системы линейных уравнений методом обратной матрицы необходимо:

1. Сформировать матрицу коэффициентов и вектор свободных членов заданной системы.

2. Решить систему, представив вектор неизвестных как произведение матрицы, обратной матрице системы, и вектора свободных членов.

Система уравнений:

Решение на рис. 24.

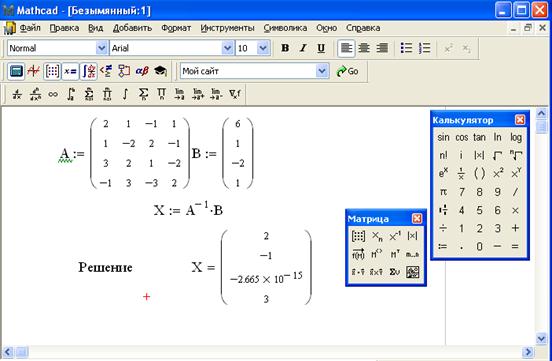
Рис 24. Решение системы методом обратной матрицы

в). Решение системы уравнений методом Гаусса основано на том, что от заданной системы переходят к эквивалентной, которая решается проще, чем исходная.

1. Сначала формируется матрица коэффициентов и вектор свободных членов заданной системы.

2. Создается расширенная матрица при помощи функции augment(A,B).

3. При помощи функции rref(A) привести расширенную матрицу к ступенчатому виду.

4. Вывести решение системы, выделив последний столбец матрицы.

5. Вычислить 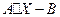, если результатом является нулевой вектор, то задача решена верно.

Система уравнений:

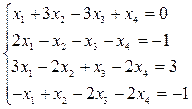
Решение на рис. 25.

Рис 25. Решение системы методом Гаусса

Ответ: .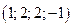

Самостоятельно:

1. Решить систему уравнений: методом Крамера, выполнить проверку

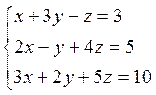
2. Решить систему уравнений: методом обратной матрицы

3. Решить систему уравнений: методом Гаусса

Дата добавления: 2014-10-31