Дискретизация, квантование и восстановление сигнала

Термины «дискретизация» и «квантование» – по существу синонимы, но так сложилось (и это общепринято), что используются они по-разному. Термин «дискретизация» применяется обычно для обозначения процедуры замены непрерывного аргумента (текуще­го времени) ограниченной последовательностью мгновенных зна­чений, т.е. перехода к дискретному времени. Термин «квантование» означает замену бесконечного множества значений непрерыв­ной функции (уровня сигнала) конечными значениями из огра­ниченного множества цифровых эквивалентов. Дискретизация и квантование реализуют аналого-цифровое преобразование, кото­рое является основой цифровой измерительной регистрации и имеет своей целью и результатом представление фрагмента непрерывно­го во времени и по уровню входного сигнала конечным числом цифровых эквивалентов (кодов).

По разным причинам обработка поступающих от АЦП цифро­вых данных не всегда выполняется в реальном времени (в темпе поступления исходных данных), поэтому необходимо промежу­точное запоминание и хранение массива кодов в некотором запо­минающем устройстве. Такая последовательность процедур диск­ретизации и квантования входного сигнала, запоминания и хра­нения кодов и является цифровой регистрацией. А поскольку в из­мерительных экспериментах требуется вполне определенная дос­товерность всех преобразований, то необходимо знание метроло­гических характеристик основных элементов структуры и всего устройства. В этом смысле речь идет о цифровой измерительной реги­страции.

В результате процедур дискретизации и квантования фрагмент непрерывного (во времени и по уровню) входного сигнала х (t)трансформируется в массив цифровых эквивалентов (кодов N_i), соответствующих дискретным отсчетам в моменты времени t ₀, t ₁, t ₂, t ₃,…,взятые с шагом дискретизации Т _д(рис. 77).

Шаг дискретизации и интервал регистрации. Конкретная форма выполнения дискретизации определяется характером сигнала, его спектральным составом, требуемой точностью последующего циф­рового преобразования и/или восстановления в аналоговую форму, задачами и алгоритмами последующей цифровой обработки информации, представления и др. Наиболее простой вид дискре­тизации – равномерная дискретизация,при которой промежуток времени между соседними отсчетами (шаг дискретизации Т _д ) по­стоянный в течение интервала регистрации Т _р.Равномерная диск­ретизация является в технической реализации наиболее простой, поэтому и применяется в большинстве случаев.

а б

Рис. 77. Дискретизация (а) и квантование (б) сигнала

В некоторых случаях используется и неравномерная дискретиза­ция, в которой шаг дискретизации в процессе регистрации не по­стоянен, а определяется особенностями сигнала (например, ско­ростью изменения сигнала, т.е. текущим значением производной сигнала).

Рис. 78 иллюстрирует понятия шага дискретизации Т _д (проме­жутка времени между соседними отсчетами – результатами ана­лого-цифрового преобразования) и интервала регистрации Т _р(об­щего времени записи).

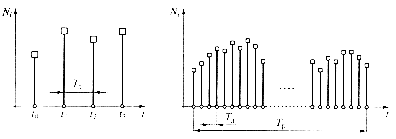
а б

Рис. 78. Иллюстрация понятия шага дискретизации (а) и интервала регистрации (б)

Поскольку значение шага Т _дперед экспериментом может зада­ваться (программироваться пользователем) в некотором диапазо­не, то возникает вопрос выбора конкретного значения шага Т _д (или частоты F _д= 1/ Т _д)дискретизации. Этот вопрос является дос­таточно важным. Чем меньше шаг Т _д(или, что то же, чем больше частота F _д),тем лучше с точки зрения последующей обработки и восстановления сигнала. Но, с другой стороны, высокая частота дискретизации означает высокую скорость заполнения памяти ре­гистратора, объем которой ограничен. Для каждого отдельного экс­перимента значение частоты F _д определяется максимально воз­можной скоростью изменения входного сигнала; способом даль­нейшего использования цифровой информации; алгоритмом обработки данных; целями и задачами восстановления входного сиг­нала по его цифровым эквивалентам; спецификой представления графической информации; требуемой окончательной погрешно­стью; объемом памяти.

В практике электрических измерений есть задачи, где требуется высокая частота дискретизации F _двходных сигналов (высокое бы­стродействие АЦП). Например, при анализе спектрального соста­ва электрического сигнала напряжения сети может потребоваться частота дискретизации F _д = (100...200) кГц (шаг дискретизации Т _ддолжен составлять, соответственно, 10...5 мкс). В то же время есть задачи, где достаточны сравнительно низкие частоты дискретиза­ции (т.е. допустимы большие значения шага Т _ддискретизации). Практически все тепловые процессы – это медленно меняющие­ся процессы, при изучении которых возможна низкая частота дис­кретизации F _д. Например, для исследования характера изменения температуры в помещении в течение трех суток (т. е. общая про­должительность записи – интервал регистрации Т _р = 72 ч) циф­ровым регистратором шаг дискретизации Т _дможет быть выбран равным 15 мин. Это означает, что по окончании записи будет заре­гистрировано (сохранено в памяти) общее число отсчетов (резуль­татов) N = 72 × 60/15 = 288. В некоторых случаях может оказаться достаточно информативным даже шаг дискретизации Т _д= 1 ч.

Восстановление и представление сигналов. Представление циф­ровых данных о зарегистрированном входном аналоговом сигнале х (t)(рис. 79, а) в графической форме возможно по-разному (рис. 79, б...г). Оно определяется требованиями задачи эксперимента, квалификацией оператора, возможностями аппаратуры и др.

а б в г

Рис. 79. Способы восстановления и представления сигнала: а – входной сигнал; б – точечное представление; в – ступенчатая аппроксимация; г – линейная интерполяция

Восстановление может происходить в самом регистраторе/ана­лизаторе или в компьютере, который выполняет обработку и пред­ставление зарегистрированных данных. Наиболее простым и не требующим дополнительных затрат является так называемое то­чечное представление (рис. 79, б),применяемое в основном в циф­ровых осциллографах и анализаторах с матричными индикатора­ми и принтерами. Основанный на способности человеческого гла­за сглаживать последовательность множества точек при небольших расстояниях между ними, этот способ дает удовлетворительное качество изображения уже при разрешающей способности экрана 1,5...2 точки/мм.

Несколько сложнее реализуется ступенчатая аппроксимация,однако при невысоких разрешающих способностях АЦП по времени и амплитуде может создаваться искаженное представление о входном сигнале. Между тем это наиболее распрост­раненный способ восстановления и представления зарегистриро­ванных сигналов.

В некоторых случаях применяется способ линейной {векторной) интерполяции (восстановление формы сигнала отрезками прямых линий), требующий определенных затрат на формирова­ние отрезков (векторов), но дающий более гладкую кривую (см. рис. 79, г).

В любом случае, чем выше частота дискретизации в процессе регистрации и чем больше разрядность аналого-цифрового пре­образования, тем точнее впоследствии может быть восстановлен сигнал по массиву зарегистрированных цифровых данных.

Дата добавления: 2014-10-15