Пример решения задачи Д1

ЗАДАЧА Д1

Механическая система состоит из грузов D₁ массой m₁=2 кг, D₂ массой m₂=6 кг и из прямоугольной вертикальной плиты массой m₃=12 кг, движущийся вдоль горизонтальных направляющих (рис. Д.1.0-Д.1.9, табл. Д1). В момент времени t₀ =0, когда система находилась в покое, под действием внутренних сил грузы начинают двигаться по желобам, представляющие собой окружности радиусов r=0,4 м и R=0,8 м.

При движении грузов угол 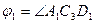изменяется по закону , а угол по закону. В табл. Д.1 эти зависимости даны отдельно для рис.0-4 и 5-9, где φ -выражено в радианах t –в секундах.

Считая грузы материальными точками и пренебрегая всеми сопротивлениями, определить закон изменения со временем величины, указанной в таблице в столбце «Найти», т.е. 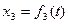и , где x₃- координата центра С₃ плиты (зависимость 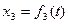определяет закон движения плиты), N- полная нормальная реакция направляющих.

Указания: Задача Д 1- на применение теоремы о движении центра масс. При этом для определения 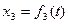составить уравнение в проекциях на горизонтальную ось Х, а для определения N- на вертикальную ось У.

Таблица Д1

Номер условия	Рис. 0-4	Рис. 5-9	Найти
,		,
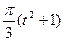
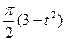
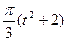
					Х3
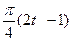
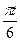
					N
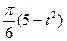
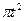
					Х3
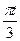
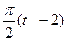
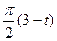
					N
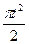
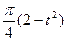
					Х3
					N
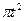
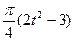
					X3
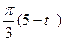
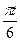
					N
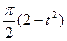
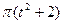
					X3
					N

Механическая система состоит из грузов D₁ массой m₁ и D₂ массой m₂ и из прямоугольной вертикальной плиты массой m₃, движущийся вдоль горизонтальных направляющих (рис. Д1). В момент времени t₀ =0, когда система находилась в покое, под действием внутренних сил грузы начинают двигаться по желобам, представляющие собой окружности радиусов r и R по законам и .

Д а н о: m₁ =6 кг, m₂ =8 кг, m₃ =12 кг, r=0,6 м, R=1,2 м, 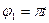рад, рад (t-в секундах). О п р е д е л и т ь: 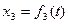- закон движения плиты, - закон изменения со временем полной нормальной реакции направляющих.

Решение. Рассмотрим механическую систему, состоящую из плиты и грузов D₁ и D₂, в произвольном положении (рис. Д 1). Изобразим действующие на систему внешние силы: силы тяжести Р₁, Р₂, Р₃ и реакцию направляющих N. Проведем координатные оси Оху так, чтобы ось у проходила через точку С₃₀, где находится центр масс плиты в момент времени t₀ =0.

а) Определения перемещения х₃. Для определения 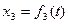воспользуемся теоремой о движении центра масс системы. Составим дифференциальное уравнение его движения в проекции на ось х.

Получим

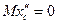или (1)

так как 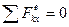, поскольку все действующие на систему внешние силы вертикальны.

Проинтегрировав уравнение (1), найдем, что , т.е. проекция скорости центра масс системы на эту ось есть величина постоянная. Так как в начальный момент времени 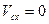, то С₁=0.

Интегрируя уравнение , получим

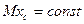(2)

т.е. центр масс системы вдоль оси Ох перемещаться не будет.

Определим значение . Из рисунка Д1 видно, что в произвольный момент времени абсциссы грузов равны соответственно , 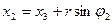. Так как по формуле, определяющей координату х_с центра масс системы, 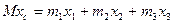, то

. (3)

В соответствии с равенством (2) координаты центра масс х_с всей системы в начальном и произвольном положении будут равны. Следовательно, учитывая, что при , получим

(4)

Отсюда получаем зависимость от времени координаты х_с.

О т в е т: 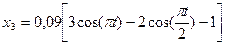м, где t –в секундах.

б) Определение реакции N. Для определения составим дифференциальное уравнение движения центра масс системы в проекции на вертикальную ось у (см. рис. Д 1):

. (1)

Отсюда получим, учтя, что , и.т.д.:

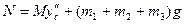. (2)

По формуле определяющей ординату у_с центра масс системы,

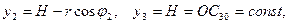получим

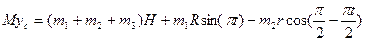
или .

Продифференцировав обе части этого равенства два раза по времени, найдем

;

.

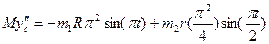Подставив это значение 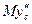в уравнение (2), определим искомую зависимость N от t.

О т в е т: , где t –в секундах, N – в ньютонах.

Дата добавления: 2014-10-31