
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Введение в математический анализ
|
|
|
|
1-40 Найти пределы функции, не пользуясь правилом опиталя.
1. а)  ; б)
; б) 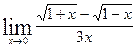 ;
;
в)  ; г)
; г) 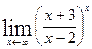 .
.
2. а)  ; б)
; б)  ;
;
в) 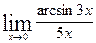 ; г)
; г) 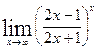 .
.
3. а)  ; б)
; б) 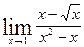 ;
;
в)  ; г)
; г)  .
.
4. а)  ; б)
; б)  ;
;
в) 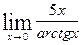 ; г)
; г) 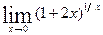 .
.
5. а)  ; б)
; б)  ;
;
в) 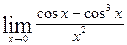 ; г)
; г) 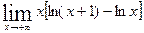 .
.
6. а) 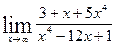 ; б)
; б) 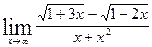 ;
;
в) 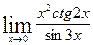 ; г)
; г) 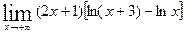 .
.
7. а) 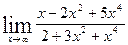 ; б)
; б) 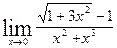 ;
;
в) 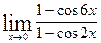 ; г)
; г) 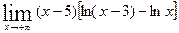 .
.
8. а) 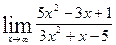 ; б)
; б) 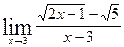 ;
;
в) 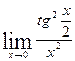 ; г)
; г) 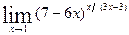 .
.
9. а) 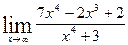 ; б)
; б) 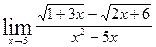 ;
;
в) 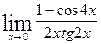 ; г)
; г)  .
.
10. а)  ; б)
; б) 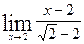 ;
;
в)  ; г.)
; г.)  .
.
11. а)  ; б)
; б) 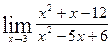 ;
;
в) 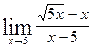 ; г)
; г) 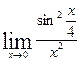 ; д)
; д) 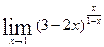 .
.
12. а)  ; б)
; б) 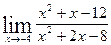 ;
;
в)  ; г)
; г) 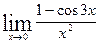 ; д)
; д)  .
.
13. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ; д)
; д) 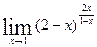 .
.
14. а) 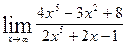 ; б)
; б)  ;
;
г)  ; г)
; г) 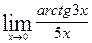 ; д)
; д)  .
.
15. а)  ; б)
; б)  ;
;
в) 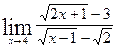 ; г)
; г) 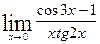 ; д)
; д) 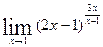 .
.
16. а)  ; б)
; б)  ;
;
в)  ; г)
; г) 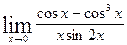 ;
;
д) 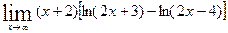 .
.
17. а)  ; б)
; б)  ;
;
в) 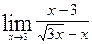 ; г)
; г)  ; д)
; д) 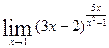 .
.
18. а) 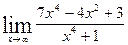 ; б)
; б) 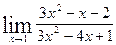 ;
;
в)  ; г)
; г)  ; д)
; д)  .
.
19. а) 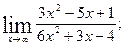 б)
б) 
в) 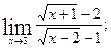 г)
г)  д)
д) 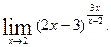
20. а)  ; б)
; б) 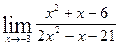 ;
;
в)  ; г)
; г) 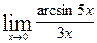 ; д)
; д)  .
.
21. а)  ; б)
; б) 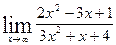 ;
;
в) 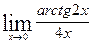 ; г)
; г) 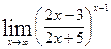 .
.
22. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
23. а) 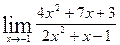 ; б)
; б)  ;
;
в)  ; г)
; г) 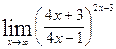 .
.
24. а)  ; б)
; б) 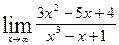 ;
;
в) 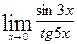 ; г)
; г)  .
.
25. а)
 ; б)
; б) 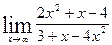 ;
;
в)  ; г)
; г) 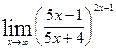 .
.
26. а) 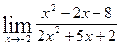 ; б)
; б) 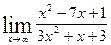 ;
;
в) 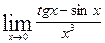 ; г)
; г) 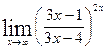 .
.
27. а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
28. а)  ; б)
; б) 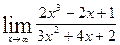 ;
;
в) 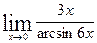 ; г)
; г)  .
.
29. а) 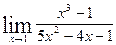 ; б)
; б) 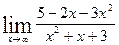 ;
;
в)  ; г)
; г) 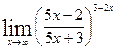 .
.
30. а) 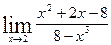 ; б)
; б)  ;
;
в 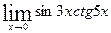 ; г)
; г) 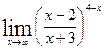 .
.
5. В каждой из задач 1-30 задана функция у=f(x) и два значения аргумента x. Требуется 1) найти пределы функции приближении к каждому из заданных значений x слева и справа; 2) установить, является ли данная функция непрерывной или разрывной для каждого из заданных значений x; 3) сделать схематический чертеж.
1. 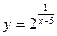 ;
;  3;
3;  5.
5.
2.  ;
;  1;
1;  3.
3.
3. 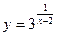 ;
;  2;
2;  4.
4.
4. 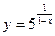 ;
;  -1;
-1;  1.
1.
5. 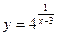 ;
;  1;
1;  3.
3.
6.  ;
;  -3;
-3;  0.
0.
7.  ;
;  -2;
-2;  0.
0.
8. 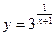 ;
;  -1;
-1;  1.
1.
9. 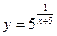 ;
;  -5;
-5;  1.
1.
10.  ;
;  -5;
-5;  -3.
-3.
11. 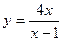 ;
; 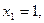

12.  ;
; 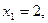

13.  ;
; 
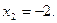
14. 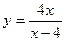 ;
; 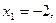

15. 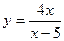 ;
; 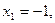

16.  ;
; 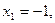

17. 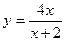 ;
; 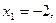

18. 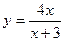 ;
; 

19. 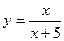 ;
; 

20. 


21. 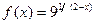


22. 


23. 


24. 
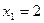
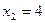
25. 
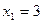
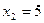
26. 
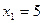

27. 


28. 
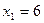

29. 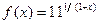


30. 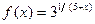


6. В задачах 1-24 функция задается различными аналитическими выражениями для различных областей изменения независимой переменной. Требуется найти точки разрыва функции, если они существуют. Сделать чертеж.
1. 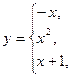

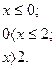
2. 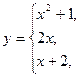

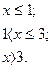
3. 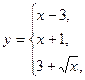


4. 

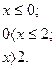
5. 

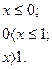
6. 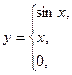

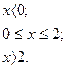
7. 


8. 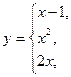

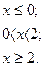
9. 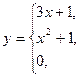

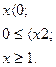
10. 


11. 

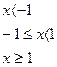
12. 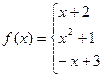

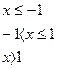
13. 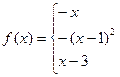

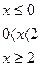
14. 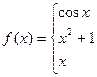


15. 


16. 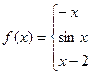

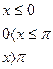
17. 


18. 

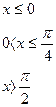
19. 

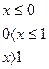
20. 


21. 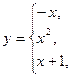

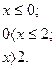
22. 

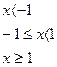
23. 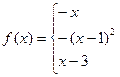

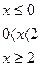
24. 


(25-30) Найти точки разрыва функции, исследовать их характер, в случае устранимого разрыва доопределить функцию «по непрерывности».
25. 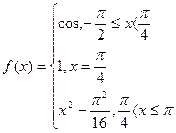
26. 
27. 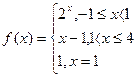
28. 
29. 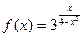
30. 
7. Производная и её приложения.
1-10. Найти производные  данных функций.
данных функций.
- а)
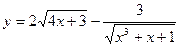 ; б)
; б) 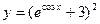 ;
;
в)  ; г)
; г)  ; д)
; д)  .
.
- а)
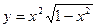 ; б)
; б) 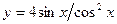 ;
;
в) 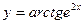 ; г)
; г) 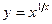 ; д)
; д)  .
.
- а)
 ; б)
; б) 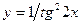 ;
;
в)  ; г)
; г) 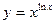 ; д)
; д) 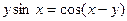 .
.
- а)
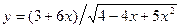 ; б)
; б)  ;
;
в) 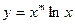 ; г)
; г) 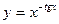 ; д)
; д)  .
.
- а)
 ; б)
; б)  ;
;
в)  ; г)
; г)  ; д)
; д) 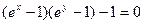 .
.
- а)
 ; б)
; б)  ;
;
в)  ; г)
; г) 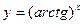 ; д)
; д)  .
.
- а)
 ; б)
; б)  ;
;
в)  ; г)
; г) 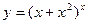 ; д)
; д) 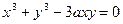 .
.
- а)
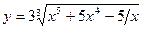 ; б)
; б) 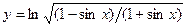 ;
;
в)  ; г)
; г) 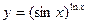 ; д)
; д)  .
.
- а)
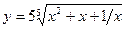 ; б)
; б)  ;
;
в)  ; г)
; г) 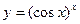 ; д)
; д)  .
.
- а)
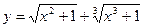 ; б)
; б) 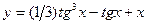 ;
;
в)  ; г)
; г) 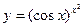 ; д)
; д) 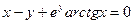 .
.
11-20. Найти  и
и 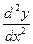 .
.
- а)
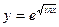 ; б)
; б) 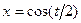 ,
, 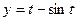 .
. - а)
 ; б)
; б)  ,
, 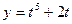 .
. - а)
 ; б)
; б) 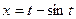 ,
,  .
. - а)
 ; б)
; б)  ,
,  .
. - а)
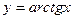 ; б)
; б)  ,
, 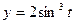 .
. - а)
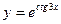 ; б)
; б) 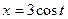 ,
, 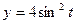 .
. - а)
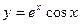 ; б)
; б)  ,
,  .
. - а)
 ; б)
; б)  ,
,  .
. - а)
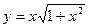 ; б)
; б) 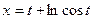 ,
,  .
. - а)
 ; б)
; б) 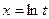 ,
,  .
. - а)
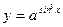 ; б)
; б) 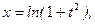 y = t – arctg t.
y = t – arctg t. - а) y = sin(2 x) б)
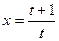 ,
, 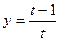 .
. - а)
 ; б) x = a cos φ, y = b sin φ.
; б) x = a cos φ, y = b sin φ. - а)
 ; б) x = et sin t, y = et cos t.
; б) x = et sin t, y = et cos t. - а)
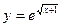 ; б) x = a cos2 φ, y = b sin2 φ.
; б) x = a cos2 φ, y = b sin2 φ. - а)
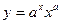 ; б) x = a(φ – sin φ), y = a(1– cos φ).
; б) x = a(φ – sin φ), y = a(1– cos φ). - а)
 ; б) x = 1 – t2, y = t – t3.
; б) x = 1 – t2, y = t – t3. - а)
 ; б)
; б) 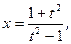
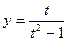 .
. - а)
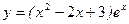 ; б)
; б) 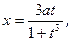
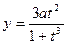 .
. - а)
 ; б)
; б)  ,
, 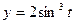 .
.
|
|
|
|
|
Дата добавления: 2014-10-31; Просмотров: 396; Нарушение авторских прав?; Мы поможем в написании вашей работы!