Формула Маклорена

Разложение функций по формуле Маклорена

Одним из основных принципов математики является пред­ставление сложного через более простое. Формула Маклорена* как раз и является реализацией этого принципа. Любые функ­ции, дифференцируемые достаточное число раз в точке х = 0, могут быть представлены в виде многочлена некоторой степе­ни. Многочлены же являются наиболее простыми элементар­ными функциями, над которыми удобно выполнять арифмети­ческие действия, вычислять значения в любой точке и т.д.

* Колин Маклорен — шотландский математик (1698 — 1746).

Итак, функцию f (x), имеющую (n + 1) производных в точке х = 0, можно представить по формуле Маклорена вместе с остаточным членом:

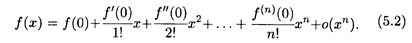
Формула (5.2) дает возможность разложить функцию f (x) по формуле Маклорена (в окрестности нуля) или, что то же самое, представить f (x) в виде многочлена, коэффициенты ко­торого вычисляются достаточно просто. Эта формула широко используется и для приближенных вычислений значений раз­личных функций; при этом погрешность вычислений оценива­ется по остаточному члену о (xⁿ).

Рассмотрим примеры разложения функций по формуле Маклорена.

Пример 1. f (x) = е^x.

Решение. Поскольку (e^x)⁽ⁿ⁾ = e^х, f⁽ⁿ⁾ (0) = е ⁰ = 1 для любого п, формула Маклорена (5.2) имеет вид

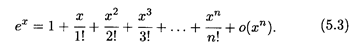
Формула (5.3) используется для вычисления числа е с лю­бой необходимой точностью. Отсюда при х = 1 получаем при­ближенное значение числа е ≈ 2,7182818....

Пример 2. f (x) = sin x.

Решение. Нетрудно проверить, что f⁽ⁿ⁾(x) = sin 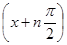; отсюда имеем

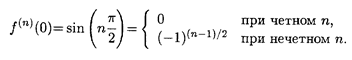
Подстановка в формулу (5.3) приводит к выражению

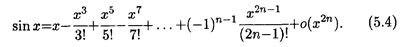
Пример 3. f (x) = cos x.

Решение. По аналогии с функцией синуса имеем 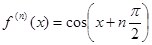, откуда получаем

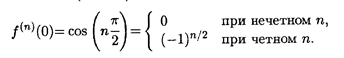
Подстановка в формулу (5.2) приводит к разложению по формуле Маклорена:

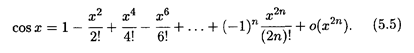
Пример 4. f(x) = ln (l + х).

Решение. Так как , то f (0) = 0, 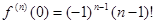; подстановка в формулу (5.2) приводит к разложению функции ln (1 + x) по формуле Маклорена (при этом 0! = 1):

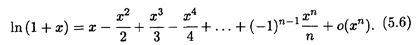
Пример 5. f (x) = (1 + x)^α, где α — вещественное число.

Решение. Производная n -го порядка имеет вид f⁽ⁿ⁾ (x) = α(α - 1)(α - 2)... (α - n +1)(1 + x) ^{α- n} , т.е. f⁽ⁿ⁾ (0) = α(α — 1)... (α - п + 1), и формула Маклорена для данной функции такова:

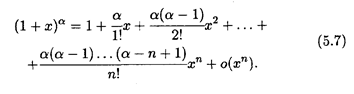
В частном случае, когда α = п — целое число, имеем f ^{(n + l)} = 0 и формула (5.7) переходит в формулу бинома Нью­тона:

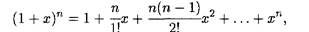
т.е. бином Ньютона является частным случаем формулы Мак­лорена.

Формула Маклорена в асимптотических формулах и вычислениях пределов функций

Формулы (5.3)-(5.7) представляют собой асимптотичес­кие формулы (или оценки) соответственно для функций e^х, sin x, cos x, ln (l + x), (1 + x) ^α при x 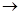0. Аналогичные раз­ложения можно получить с использованием формулы (5.2) и для других функций. Асимптотические формулы эффективно применяются при вычислении пределов функций. Покажем это на примере.

Пример 6. Найти .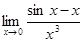

Решение. Применяя формулу (5.2) при п = 2, получаем

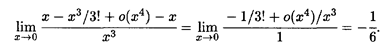
Дата добавления: 2014-10-15