Применение в экономике

Предельные показатели в микроэкономике

Приведем примеры двух предельных показателей в микро­экономике.

1. Первый из них связан с зависимостью себестоимости С произведенной продукции от ее объема Q: С = f(Q). Так называемая предельная себестоимость характеризует себестои­мость Δ C прироста продукции Δ Q:

В предположении о непрерывной зависимости Δ С от Δ Q естес­твенно напрашивается замена разностного отношения в (5.13) его пределом:

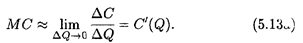
Обычно в приложениях с использованием аппарата математи­ки под предельной себестоимостью понимают именно величину (5.13а).

Например, пусть зависимость издержек производства от объема выпускаемой продукции выражается формулой

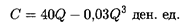
Определим средние и предельные издержки при объеме про­дукции Q = 15 ден. ед.

А) Функция средних издержек на единицу продукции опре­деляется по формуле 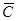= C/Q, или в нашем случае

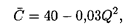
откуда 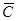(15) = 40 - 0,03 ∙ 225 = 33,25 ден. ед.

Б) Предельные издержки определяются, согласно (5.13а), по формуле

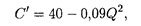
откуда при Q = 15 получаем С' (15) = 19,75 ден. ед.

Иными словами, при средних издержках на производство единицы продукции в 33,25 ден. ед. дополнительные затраты на производство единицы дополнительной продукции составят 19,75 ден. ед. и не превысят средних издержек.

2. В анализе и прогнозах ценовой политики применяется понятие эластичности спроса. Пусть D = f (Р) — функция спроса от цены товара Р (см. п. 3.1). Тогда под эластичнос­тью спроса понимается процентное изменение спроса при из­менении цены товара на один процент:

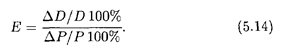
Как и в предыдущем случае, в случае непрерывной зависимос­ти Δ D от Δ Q удобно перейти к пределу при Δ Р 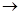0:

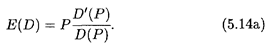
Аналогичное понятие можно ввести и для функции предло­жения S(P). Напомним, что функция D(P) убывает, а функция S(P) возрастает с ростом цены Р.

Укажем некоторые свойства эластичности. Как следует из формулы (5.14а), ее можно выразить так:

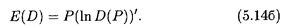
Из равенства (5.14 б) следует, что E(D) обладает свойствами логарифма, а значит,

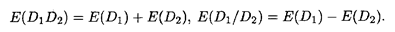
Заметим, что поскольку функция D(P) убывающая, то D'(P) < 0, а тогда согласно формуле (5.14а) и E(D) < 0. Напротив, поскольку функция предложения возрастающая, то соответствующая эластичность E(S) > 0.

Различают три вида спроса в зависимости от величины |E(D)|:

а) если |E(D)| > 1 (E(D) < -1), то спрос считается элас­тичным;

б) если |E(D)| = 1 (E(D) = -1), то спрос нейтрален;

в) если | E(D)| < 1 (E(D) > -1), то спрос неэластичный.

Рассмотрим два примера из этой области.

Пример 1. Пусть функция спроса описывается формулой

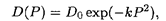
где D₀ и k — известные величины. Найти, при каких значениях цены Р спрос будет эластичным.

Решение. Согласно формуле (5.14а) составляем выраже­ние для E(D):

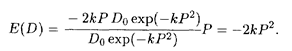
Для того чтобы спрос был эластичным (случай а), необходимо, чтобы выполнялось неравенство

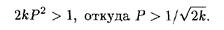
Пример 2. Найти изменение выручки с увеличением цены на товар при разных вариантах эластичности спроса.

Решение. Выручка I равна произведению цены Р на товар на величину спроса D:

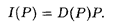
Найдем производную этой функции:

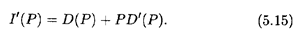
Теперь проанализируем все варианты эластичности спроса, приведенные выше, с учетом формулы (5.14а).

1) E(D) < -1; тогда, подставляя (5.14а) в это неравенст­во, получаем, что правая часть уравнения (5.15) отрицательна. Таким образом, при эластичном спросе повышение цены Р ве­дет к снижению выручки. Напротив, снижение цены на товар увеличивает выручку.

2) E(D) = -1. Из (5.14а) следует, что правая часть (5.15) равна нулю, т.е. при нейтральном спросе изменение цены на товар не влияет на выручку.

3) E(D) > -1. Тогда I'(P) > 0, т.е. при неэластичном спросе повышение цены Р на товар приводит к росту выручки.

Понятие эластичности распространяется и на другие обла­сти экономики. Рассмотрим один характерный пример.

Пример 3. Пусть зависимость между себестоимостью продук­ции С и объемом Q ее производства выражается формулой

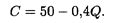
Требуется определить эластичность себестоимости при выпус­ке продукции Q = 30 ден. ед.

Решение. По формуле (5.14а) получаем

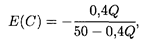
откуда при Q = 30 искомая эластичность составит около —0,32, т.е. при данном объеме выпуска продукции его увеличение на 1% приведет к снижению себестоимости примерно на 0,32%.

Максимизация прибыли

Пусть Q — количество реализованного товара, R(Q) — функция дохода; C(Q) — функция затрат на производство то­вара. В реальности вид этих функций зависит в первую оче­редь от способа производства, организации инфраструктуры и т.п. Прибыль от реализации произведенного товара дается формулой

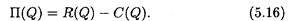
В микроэкономике известно утверждение: для того чтобы прибыль была максимальной, необходимо, чтобы предельный доход и предельные издержки были равны. Оба упомянутых предельных показателя определяются по аналогии с (5.14а), так что этот принцип можно записать в виде R'(Q) = C'(Q). Действительно, из необходимого условия экстремума для функ­ции (5.16) следует, что П'(Q) = 0, откуда и получается основ­ной принцип.

Пример 4. Найти максимум прибыли, если доход и издержки определяются следующими формулами:

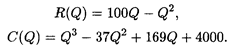
Решение. Согласно (5.16), прибыль П(Q) = - Q³ + 36 Q² - 69 Q — 4000. Приравнивая производную функции прибыли к нулю, получаем уравнение

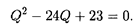
Корни этого уравнения Q₁ = 1, Q₂ = 23. Проверка показы­вает, что максимальная прибыль достигается при Q = 23: П_mах = 1290.

Закон убывающей эффективности производства

Этот закон утверждает, что при увеличении одного из ос­новных факторов производства, например капитальных затрат К, прирост производства начиная с некоторого значения К яв­ляется убывающей функцией. Иными словами, объем произве­денной продукции V как функция от К описывается графиком со сменой выпуклости вниз на выпуклость вверх.

Пример 5. Пусть эта функция дается уравнением

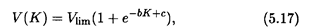
где b и с — известные положительные числа (они определя­ются прежде всего структурой организации производства), а V_lim — предельно возможный объем выпускаемой продукции. Нетрудно подсчитать, что вторая производная функции (5.17) имеет вид

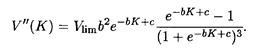
Критическая точка находится из условия V"(K) = 0, откуда

График функции (5.17) приведен на рис. 5.10. В точке пе­региба (5.18) выпуклость графика функции вниз меняется на выпуклость вверх. До этой точки увеличение капитальных за­трат приводит к интенсивному росту объема продукции: темп прироста объема продукции (аналог первой производной) воз­растает, т.е. V"(K) > 0. При К > К _cr темп прироста объема выпускаемой продукции снижается, т.е. V"(K) < 0, и эффек­тивность увеличения капитальных затрат падает.

Таким образом, в стратегии капиталовложений оказывает­ся очень важным моментом определение критического объема затрат, сверх которого дополнительные затраты будут приво­дить все к меньшей отдаче при данной структуре организа­ции производства. Зная этот прогноз, можно пытаться совер­шенствовать и менять структуру организации производства: "улучшать" показатели b, с и V _lim в сторону повышения эф­фективности капиталовложений.

Дата добавления: 2014-10-15