Нахождение оптимальных путей транспортировки грузов при нестабильной загрузке дорог

Транспортная параметрическая задача

Задача формулируется следующим образом: для всех зна­чений параметра δ ≤ λ ≤ φ, где δ, φ — произвольные дейст­вительные числа, найти такие значения x_ij (i = 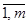; j =), которые обращают в минимум функцию

при ограничениях:

Пользуясь методом потенциалов, решаем задачу при λ = δ до получения оптимального решения. Признаком оптимально­сти является условие:

u_i + v_j — [ c'_ij + λ с"_ij) ≤ 0 для незанятых клеток

и u_i + v_j = с' _ij + λ с''_ij для занятых клеток,

где u_i, v_j — потенциалы строк, столбцов распределительной таблицы.

Условие совместимости транспортной задачи запишется в виде

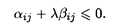
Значения α_ij и β_ij определяются из условия

где u'_i, v'_i, u"_j, v"_j определяются из систем уравнений

Значения λ находятся в пределах λ₁ ≤ λ ≤ λ₂:

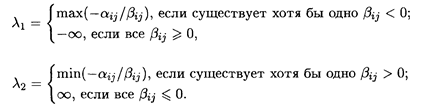
Алгоритм решения.

1) Задачу решаем при конкретном значении параметра λ = δ до получения оптимального решения.

2) Определяем α_ij и β_ij.

3) Вычисляем значения параметра λ.

4) Если λ < φ, производим перераспределение поставок и получаем новое оптимальное решение. Если λ = φ, то процесс решения окончен.

Имеются три поставщика однородного товара с объемами поставок: а ₁ = 100 т, а ₂ = 200 т, a ₃ = 100 т и четыре потреби­теля с объемами потребления b ₁ = - 80 т, b ₂ = 120 т, b ₃ = 150 т, b ₄ = 50 т. Стоимость транспортных расходов изменяется в определенном диапазоне в зависимости от загрузки дороги и задана матрицей

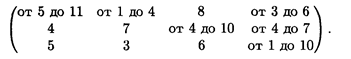
Определить оптимальное решение перевозок, обеспечиваю­щее минимальные транспортные затраты.

Решение. В матрицу расходов введем параметр λ, где 0 ≤ λ ≤ 3. Получим

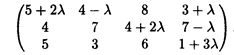
Полагая λ = 0, решаем задачу методом потенциалов, опре­делим оптимальное решение перевозок. Распределительная таблица этого решения будет иметь вид табл. 25.5.

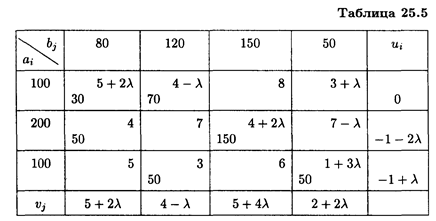
В таблице u_i и v_j — потенциалы строк и столбцов. Для занятых клеток они определяются из условия

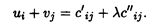
Полагая u ₁ = 0, v ₁ + и ₁ = 5 + 2λ, получаем v ₁ = 5 + 2λ,

v ₂ + и ₁ = 4 — λ, откуда v ₂ = 4 — λ;

v ₁ + u ₂ = 4 или 5 + 2λ + u ₂ = 4, откуда и ₂ = -1 - 2λ;

v ₃ + u ₂ = 4 + 2λ или -1 – 2λ + v ₃ = 4 + 2λ, v ₃ = 5 + 4λ.

Аналогично находим, что u ₃ = -1 + λ, v ₄ = 2 + 2λ.

Оценки свободных клеток находим по формуле

Имеем

Аналогично находим, что Δ₂₄ = -6 + λ, Δ₃₁ = -1 + 3λ, Δ₃₃ = -2 + 5λ.

Решение, полученное при λ = 0, является оптимальным для всех значений параметра λ, удовлетворяющих условию

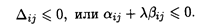
Имеем

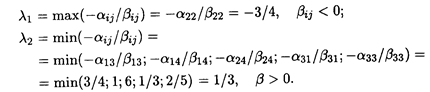
Так как по условию задачи λ ≥ 0, то оптимальное решение сохраняется при 0 ≤ λ ≤ 1/3. При этом минимальная стои­мость транспортных расходов составляет

Таким образом, при λ [0; 1/3] L (X ₁)_min = 1430 + 440λ и

Чтобы получить оптимальное решение при λ ≥ 1/3, пере­распределим поставки товаров в клетку (3, 1), где λ₂ = 1/3. Вновь полученное распределение представлено в табл. 25.6.

Находим оценки свободных клеток:

Определим пределы изменения λ:

Полученное в таблице оптимальное решение сохраняется при 1/3≤ λ≤ 1/2. При этом L(X ₂ ) _min = 1460 + 350λ. Итак,

Перераспределим поставки грузов в клетку (3, 3), где λ₂ = 1/2. Получим новое распределение (табл. 25.7). Находим оценки свободных клеток:

Определим пределы изменения λ:

Оптимальное решение сохраняется при 1/2 ≤ λ ≤ 1. При этом L (Х ₃)_min = 1490 + 290λ. Итак,

Перераспределим поставки товаров в клетку (1, 4), где λ₂ = 1 (табл. 25.8).

Оценки свободных клеток:

Пределы изменения λ:

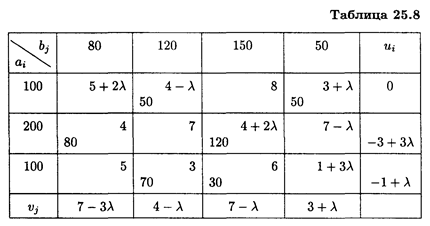
Полученное в предыдущей таблице оптимальное решение сохраняется при λ ≤ 7/5. При этом L(Х ₄ ) _min = 1540 + 240λ. Итак,

Перераспределим поставки грузов в клетку (2, 4), где λ₂ = 7/5 (табл. 25.9).

Оценки свободных клеток:

Пределы изменения λ:

Оптимальное решение сохраняется при 7/5≤ λ≤ 3. При этом L(X ₅ ) _min = 1890 – 10λ. Итак,

Дата добавления: 2014-10-15