Модель запасов, включающая штрафы

Рассмотрим основную модель, допускающую возможность существования периодов дефицита, который покрывается при последующих поставках, и штрафов за несвоевременную по­ставку.

Пусть предприятие должно поставить q ед. товара в тече­ние каждого промежутка времени L, за единицу времени по­ставляется g ед. товара (q = Lg).

Предположим, что в начале каждого периода L предприя­тие делает запас, равный k. Это означает, что в течение пе­риода будет наблюдаться дефицит товара и некоторое время поставки не будут осуществляться. Невыполненные заявки бу­дут накапливаться до максимальной величины q — k и будут удовлетворены, как только поступит следующая партия това­ров в количестве q.

За то, что товары доставляются предприятием позже необ­ходимого срока, на предприятие налагается штраф, который зависит от того, насколько была задержана поставка. Такая модель целесообразна, поскольку иногда выгоднее заплатить штраф, чем расходовать дополнительные средства на хране­ние запасов, превышающих величину k.

Задача управления запасами состоит в том, чтобы выбрать такое значение k, которое ведет к минимизации всех затрат, включая затраты на хранение и штрафы.

График изменения запасов модели представлен на рис. 33.5.

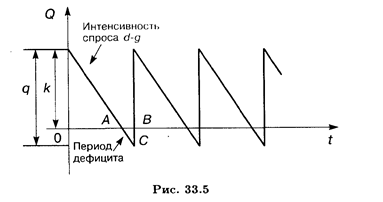
Для определения оптимального значения k обозначим:

h — издержки хранения единицы товара за единицу вре­мени;

р — затраты на штраф в расчете на единицу товара за один день отсрочки.

Найдем издержки одного цикла:

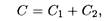
где С ₁ — общие издержки содержания запасов; С ₂ — общие затраты на штраф.

Так как товары находятся на складе в течение периода ОА (см. рис. 33.5), средний уровень запасов за этот период равен k/2. Если продолжительность периода ОА равна k/g, то

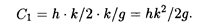
Так как штраф выплачивается в течение периода АВ = (q — k)/g, общее число "товаро-дней", на которые налагается штраф, равно площади треугольника АВС. Площадь состав­ляет

откуда С ₂ = p(q — k) ² / 2 g.

Окончательно

Найдем dC/dk и, решив уравнение dC/dk = 0, получим оптимальное значение:

Взяв k _опт в качестве уровня запасов в начале каждого цикла при условии, что невыполненные заявки будут удовлетворены, сведем суммарные расходы С к минимуму:

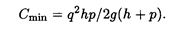
Дата добавления: 2014-10-15