Решение экономических задач с использованием моделей управления запасами

Решим задачу с применением основной модели управления запасами.

Пример 1. Интенсивность равномерного спроса составляет 2000 телевизоров в год. Организационные издержки для од­ной партии составляют 20 тыс. р. Цена единицы товара рав­на 1 тыс. р., а издержки содержания телевизоров составляют 0,1 тыс. р. за один телевизор в год.

Найти оптимальный размер партии, число поставок и про­должительность цикла.

Решение. По условию задачи g = 2000, b = 20, s = 1, h = 0,1.

Общие издержки в течение года:

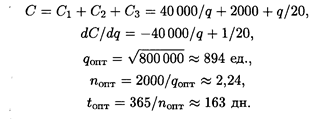
Ответ. Оптимальный размер партии составляет 894 те­левизора, число поставок — 2,24, продолжительность цикла — 163 дня.

Рассмотрим задачу с применением модели производствен­ных поставок.

Пример 2. Интенсивность равномерного спроса выпускаемых фирмой видеомагнитофонов составляет 2000 шт. в год. Органи­зационные издержки равны 20 тыс. р. Цена видеомагнитофона составляет 1 тыс. р., издержки хранения равны 0,1 тыс. р. в расчете на один видеомагнитофон в год. Запасы на складе по­полняются со скоростью 4000 видеомагнитофонов в год. Произ­водственная линия начинает действовать, как только уровень запасов на складе становится равным нулю, и продолжает ра­боту до тех пор, пока не будет произведено q видеомагнитофо­нов.

Найти размер партии, который минимизирует все затраты. Определить число поставок в течение года, время, в течение которого продолжается поставка, продолжительность цикла, максимальный уровень запасов и средний уровень запасов при условии, что размер поставки оптимален.

Решение. Данная модель задачи является моделью произ­водственных поставок со следующими параметрами:

График изменения запасов представлен на рис. 33.6.

Число партий в течение года:

Продолжительность поставки:

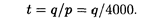
Продолжительность цикла:

Максимальный уровень запасов:

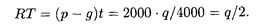
Средний уровень запасов:

Уравнение издержек:

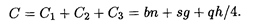
Решив уравнение dC/dq = 0, получим q _опт = = 1265 видеомагнитофонов.

Найдем оптимальные значения поставок, продолжительность поставки, продолжительность цикла:

Ответ. За каждую поставку необходимо доставлять на склад 1265 видеомагнитофонов, оптимальное число поставок составляет 1,6, продолжительность поставки — 115 дней, про­должительность цикла — 230 дней.

Дата добавления: 2014-10-15