Основные алгоритмические конструкции

Элементарные шаги алгоритма можно объединить в следующие алгоритмические конструкции: линейные (последовательные), разветвляющиеся, циклические ( типыалгоритмов )

Линейным называется алгоритм, не содержащий условий. Примером линейного алгоритма может служить описание последовательности действий для вычисления какого-либо арифметического выражения по формуле.

Пример: y = a + b

Y= a + b

Разветвляющимся (с логическим выбором) называется алгоритм, который содержит хотя бы одно условие.

Пример: y=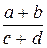

y = (a+b)/(c+d)

Да Нет

Циклическим называется такой алгоритм, часть действий в котором повторяется неоднократно. Такие повторяющиеся действия в алгоритме получили название «цикл». Циклические алгоритмы содержат условия, поэтому они составляют подкласс разветвляющихся алгоритмов.

Массив – это упорядоченная по номерам последовательность однородных элементов. Различаются массивы своей организацией. Они могут быть одномерными (векторными), двумерными (матрицами), трехмерными (кубами) и т.д.

Одномерный массив определяется именем – идентификатором массива и граничной парой.

Например: X[K..N], здесь Х – идентификатор массива, К – номер первого элемента, N – номер последнего элемента.

Пример: найти сумму элементов одномерного массива X[1..N].

i = 1

i = i + 1

S= S + x (i)

Да Нет

Дата добавления: 2014-10-31