Теория познания 2 страница

Можно было бы подумать, что математические объекты этого типа следовало бы поместить среди Форм или άρχαί и что Платон мог бы приравнять научное знание геометра к самому νόησις, однако он весьма пылко отказывается сделать это, и поэтому предположение о том, что Платон подгонял свои гносеологические доктрины под сравнение с линией, которая их разделяет (как пытались доказать некоторые ученые), совершенно неверно. Скорее верно предположение о том, что Платон действительно верил в существование «промежуточного звена», то есть объектов άρχαί, которые в то же время находятся в подчиненном положении по отношению к διάνοια и потому являются объектами рассудка, а не ума. В конце шестой книги «Государства» Платон говорит, что геометры не могут постигнуть область умопостигаемого умом, поскольку они не поднимаются выше своих гипотетических предпосылок. Поэтому «они и не могут дойти до нее умом, хотя она вполне умопостигаема, если постичь ее первоначало». Последние слова Платона свидетельствуют о том, что различия двух верхних отрезков линии соответствуют различиям состояний души, а не только различиям своих объектов. И Платон с жаром утверждает, что рассудок занимает промежуточное положение между мнением δόςα и чистым разумом διάνοια.

Этот вывод подтверждается изучением вопроса о гипотезах. Неттлшип полагал, что Платон имеет в виду то, что математик принимает свои постулаты и аксиомы за истину: сам он их не проблематизирует, а если кто–то другой подвергает их сомнению, математик говорит, что он не желает обсуждать этот вопрос. Платон употребляет слово «гипотеза» не для обозначения суждения, которое считается истинным, но которое может и не быть таковым, а для обозначения суждения, которое он считает самообоснованным и потому не нуждающимся в оправдании и объяснении его связи с бытием. Однако следует отметить, что примеры «гипотез», приведенные в 510 с, представляют собой скорее примеры сущностей, чем суждений, и что Платон говорит скорее об опровержении гипотез, чем о сведении их к самообоснованным или самоочевидным предпосылкам. Более подробное объяснение этого вопроса будет приведено в конце этого раздела.

В своей «Метафизике» Аристотель рассказывает нам, что, по мнению Платона, математические сущности располагаются «между формами и чувственными вещами». «Далее он говорит, что помимо чувственных вещей и форм существуют объекты математики, занимающие промежуточное положение. Они отличаются от чувственных вещей своей вечностью и неизменностью, а от Форм тем, что среди них много похожих, в то время как каждая форма уникальна и неповторима». Учитывая это высказывание Аристотеля, вряд ли было бы справедливо соотносить различие двух отрезков верхней части линии только с состоянием души – должно быть и различие в объектах. (Можно было бы различать только состояния души, если бы τά μαθηματικά объекты математики сами по себе соответствовали бы тому же самому отрезку, что и αί άρχαί, и математик рассматривал бы их как «материалы» для своих гипотез, а затем делал бы выводы. Тогда его душа находилась бы в таком состоянии, которое Платон называл рассудком, ибо он рассматривал бы свои постулаты как самоочевидные, не задавая дополнительных вопросов, и делал бы выводы с помощью наглядных схем. В этом случае математик имел бы дело не со схемами, как таковыми, а с идеальными математическими объектами, поэтому, если бы он рассматривал свои предположения «в связи с первоначалами», он постигал бы их не рассудком, а умом, хотя истинные объекты его размышлений, то есть идеальные математические объекты, оставались бы теми же самыми. Такое толкование, которое связывает два верхних отрезка линии только с состоянием души, подтверждается утверждением Платона, что математические вопросы, рассматриваемые в связи с первоначалами, принадлежат к области чистого разума. Однако замечания Аристотеля на эту тему, если они, конечно, правильно отражают мысль Платона, отрицают это толкование, ибо Аристотель был уверен, что Платоновы математические сущности занимают положение между αί άρχαί и τά δρατά.

Если Аристотель прав и Платон действительно думал, что объекты математики образуют особый вид объектов, отличающийся от других видов, в чем же тогда заключается это отличие? У нас нет нужды рассматривать различие между объектами математики и объектами нижней части линии, τά δρατά, ибо и без того ясно, что математики имеют дело с идеальными и совершенными объектами мысли, а не с эмпирическими окружностями или линиями, к примеру колесами повозки или обручами или даже с геометрическими схемами, как таковыми, то есть с чувственными частностями. Вопрос, таким образом, сводится к следующему: в чем на самом деле заключается различие между объектами математики как объектами рассудка и архетипами как объектами ума?

Естественное толкование высказывания Аристотеля в «Метафизике» заключается в том, что, согласно Платону, математик говорит об умопостигаемых частностях, а не о чувственных частностях и не об универсальных сущностях. К примеру, если геометр утверждает, что две окружности пересекаются, он имеет в виду не какие–то конкретные окружности, нарисованные на чертеже, и не кругообразность, как таковую, – как могла бы кругообразность пересечься с другой кругообразностью? Он говорит об умопостигаемых окружностях, из которых многие похожи, как утверждает Аристотель. И снова сказать, что «два плюс два равно четырем», – вовсе не то же самое, что спросить, что произойдет, если к двоичности прибавить ее саму – эта фраза лишена смысла. Эта мысль подтверждается утверждением Аристотеля, что для Платона «существует некая первая двоица и первая троица и что числа несопоставимы друг с другом»8. Для Платона целые числа, включая 1, образуют такой ряд, в котором 2 состоит не из двух единиц, а является уникальной численной формой. Это все равно, что сказать, что целое число 2 – это двоичность, которая не слагается из двух «единичностей». По–видимому, Платон отождествлял эти целые числа с Формами. И если нельзя сказать, что целое число 2 имеет много подобных (не больше, чем кругообразностей), ясно, что математик, который не поднимается до конечных формальных принципов, в действительности имеет дело с множеством целых чисел 2 и с множеством окружностей. Когда же геометр говорит о пересекающихся окружностях, он имеет дело не с чувственными частностями, а с умопостигаемыми объектами. И поскольку многие из них похожи, они не являются настоящими универсалиями, но образуют вид особых умопостигаемых частностей, располагающихся «выше» чувственных частностей, но «ниже» истинных универсалий. Отсюда вытекает, что Платоновы математические объекты образуют особый вид умопостигаемых частностей.

Профессор А.Э. Тейлор, если я его правильно понял, считает, что математические объекты относятся к области идеальных пространственных величин. Он указывает, что свойства окружностей, например, можно изучать с помощью численных уравнений, но они сами по себе не являются числами, поэтому они не относятся к самому верхнему отрезку линии, где располагаются αί άρχαί или Формы, которые Платон отождествлял с Числами. С другой стороны, идеальные пространственные величины, то есть объекты, изучаемые геометрией, не являются чувственными объектами, поэтому они не могут принадлежать к области τά δρατά. Поэтому они занимают промежуточное положение между Числами–Формами и Чувственными Объектами. Я готов согласиться с тем, что это справедливо по отношению к объектам, которые изучает геометрия (например, пересекающимся окружностям и т. д.), но можно ли исключить из области τά μαθηματικά объекты, которые изучает арифметика? Ведь Платон, говоря о тех, кто постигает рассудком, имел в виду не только тех, кто изучает геометрию, но и тех, кто изучает арифметику и родственные науки. Однако из этого вовсе не следует, что объекты, изучаемые математикой, ограничиваются лишь идеальными пространственными величинами. Мы думаем, что Платон должен был бы ограничить подобным образом сферу математических сущностей, однако мы должны принимать во внимание не то, что он должен был бы утверждать, но и то, что он говорил на самом деле.

Вероятнее всего, он понимал под математическими сущностями объекты и геометрии, и арифметики (и не только этих двух наук, как следует из замечания о «родственных науках»). Как же нам тогда понимать замечание Аристотеля о том, что для Платона числа не складываются друг с другом? Я думаю, что мы должны учесть это замечание, помня, что Платон ясно видел, что числа сами по себе уникальны. С другой стороны, также ясно, что мы можем складывать группы или классы объектов и говорим о числе как о характеристике класса. Числа мы складываем, но они обозначают классы конкретных объектов, хотя они являются объектами, но не чувственного восприятия, а разума. Поэтому о них можно говорить как об умопостигаемых частностях, которые принадлежат к области математики, так же как и идеальные пространственные величины геометрии. Аристотелева теория числа может быть сама по себе ошибочной, и потому он мог в определенном смысле неправильно истолковать теорию Платона; но если он заявлял со всей определенностью, что Платон выделил промежуточный класс математических сущностей, то вряд ли он ошибался. Более того, высказывания самого Платона не оставляют места для сомнений, не только потому, что он действительно выделил такой класс, но и потому, что он вовсе не собирался ограничить этот класс только лишь идеальными пространственными величинами.

(Утверждение Платона о том, что математические гипотезы – он упоминает «чет и нечет, фигуры, три вида углов и прочее в том же роде», – взятые в связи с главным принципом, познаются на более высоком уровне мышления, а также его утверждение, что этот уровень мышления связан с главным принципом, что самоочевидно, позволяют предположить, что он приветствовал бы современные попытки свести чистую математику к их логическим основаниям.)

Осталось вкратце рассмотреть самый верхний отрезок линии. Состояние ума, νόησις, соответствующее ему, – это состояние ума человека, использующего в качестве отправной точки гипотезы рассудка и поднимающегося до первых принципов. Более того, в этом процессе (иными словами, в диалектическом процессе) ум не пользуется «никакими «образами», но лишь самими идеями в их взаимном отношении, и его выводы относятся только к ним». Четко осознав главные принципы, ум делает из них выводы, по–прежнему используя только абстрактные рассуждения, но отнюдь не чувственные образы9. Объекты, соответствующие уму, – это διάνοια главные принципы или Формы. Это не только гносеологические, но и онтологические принципы, и более подробно они будут рассмотрены позже, однако следует упомянуть следующее. Если бы вся проблема заключалась только в том, чтобы познать главные принципы с помощью рассудка (как, например, в современных попытках редукции математики к ее логическим основаниям), тогда можно было бы без труда понять, что имел в виду Платон, но он называл диалектику способом «опровержения гипотез»10, что очень сильно сказано, поскольку хотя диалектика и способна показать необходимость пересмотра математических постулатов, однако трудно понять, хотя бы на первый взгляд, как она может опровергать гипотезы. Мысль Платона станет яснее, если мы рассмотрим одну конкретную гипотезу, которую он упоминает, – четные и нечетные числа. Платон признает существование чисел, которые не являются ни четными, ни нечетными, то есть иррациональных, а в «Послезаконии» он требует признать в качестве чисел квадраты и третьи степени «иррациональных величин». Если это так, то задача диалектики заключается в том, чтобы показать, что традиционная гипотеза математики, гласящая, что иррациональных чисел нет, а есть целые числа, которые могут быть либо четными, либо нечетными, не совсем соответствует истине. Опять же Платон отказался признать пифагорейскую идею «единичной точки» и называл точку «началом линии». По его мнению, единичная точка, то есть точка, имеющая свой собственный размер, – это выдумка геометров, «геометрическая фикция»11, и эту гипотезу следует отбросить.

3. В седьмой книге «Государства» Платон иллюстрирует свою гносеологическую теорию знаменитой аллегорией пещеры. Я вкратце опишу эту аллегорию, поскольку из нее ясно видно (если требуются еще какие–то доказательства), что восхождение души от нижних отрезков линии к верхним представляет собой гносеологический прогресс и что Платон рассматривал этот процесс не как непрерывную эволюцию, а скорее как ряд «переходов» от менее адекватного к более адекватному когнитивному состоянию.

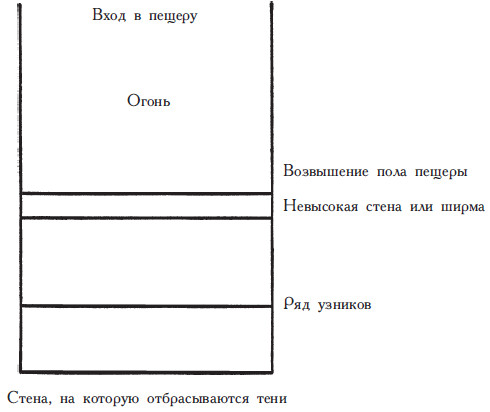
Платон предлагает нам представить подземную пещеру, имеющую выход наружу. В этой пещере живут человеческие существа, у которых с малых лет на ногах и на шее оковы, которыми они прикованы так, что обращены лицом к стене, и видят они только то, что перед глазами. Они никогда не видели солнечного света. За спиной у них на возвышении горит огонь, а между огнем и узниками располагается невысокая стена, нечто вроде ширмы. За этой стеной проносят статуи людей, изображения живых существ и другие вещи – они как бы проплывают над стеной. Узники, лица которых обращены к стене пещеры, не видят ни друг друга, ни предметов, проносимых за их спинами, они видят только свои тени и тени, отбрасываемые движущимися объектами на стену пещеры. Итак, они видят только тени.

Эти узники олицетворяют бо́льшую часть человечества, тех людей, которые проводят всю свою жизнь в состоянии εικασία, воспринимая только тени реального и слыша только эхо истины. Они имеют превратное представление о мире, искаженное «их собственными страстями и предрассудками, а также страстями и предрассудками других людей, передаваемыми им с помощью языка и риторики». И хотя их ум находится на том же уровне развития, что и у детей, они держатся за свои искаженные взгляды со всем упорством взрослых и не имеют никакого желания вырваться из своей тюрьмы. Более того, если бы их вдруг случайно освободили и велели бы взглянуть на реальное положение вещей, от которого они раньше видели только тени, они были бы ослеплены ярким светом и решили бы, что тени гораздо более реальны, чем настоящие предметы.

Однако если один из освобожденных узников привыкнет к свету, то через какое–то время он сможет воспринимать уже конкретные чувственные объекты, от которых он раньше видел только тени. Освещенные светом огня (олицетворяющим солнце), его сотоварищи предстают перед ним уже совсем в другом виде. Мы можем сказать, что ум такого человека достиг состояния πίστις, поскольку он воспринимает уже не мир теней (то есть мир предрассудков, страстей и софистики, а реальный мир, хотя мир умопостигаемых, чувственных реальностей он еще постичь не в состоянии. Он понимает, что все его сотоварищи – пленники, пленники страстей и софистики. Более того, если он проявит настойчивость и выйдет из пещеры на солнечный свет, то увидит светлый мир освещенных солнцем объектов (представляющих собой умопостигаемые реальности), и, наконец, правда не без труда, он сможет увидеть само солнце, которое олицетворяет Идею Бога, Высшей Формы, «всеобщую причину всех вещей, правильных и прекрасных, – источник истины и разума»12. Тогда он достигнет состояния νόησις. (К этой Идее Бога, а также к политическим взглядам Платона, изложенным в «Государстве», мы вернемся позже.)

Платон отмечает, что если тот, кто увидит солнечный свет, вернется в пещеру, то не увидит ничего из–за темноты, а узники будут над ним смеяться. Если же он попытается кого–то освободить и вывести на свет, то узники, любящие темноту и считающие тени истинной реальностью, приговорят его к смерти, если сумеют, конечно, поймать. Здесь мы видим явный намек на судьбу Сократа, который стремился просвещать тех, кто хотел его слушать, показывая, в чем заключается истина и роль разума. Он хотел, чтобы они освободились от власти предрассудков и софистики.

Эта аллегория свидетельствует, что Платон считал «восхождение» души в область умопостигаемого прогрессом, но не автоматическим и непрерывным, а требующим усилий и дисциплины ума. Отсюда то огромное значение, которое он придавал образованию, в процессе которого молодые люди впитывают в себя вечные и абсолютные истины и ценности, спасаясь тем самым от мира теней, где царят ошибки, фальшь, предрассудки, хитросплетения софистов, забвение истинных ценностей и т. д. Особенно важно такое образование для тех, кто будет управлять государством, ведь, пребывая в состоянии εικασία или πίστις, государственные мужи и правители напоминают поводырей слепцов, которые сами ничего не видят, а ведь крушение государственного корабля приносит больше бед, чем гибель небольшой лодчонки. Таким образом, интерес Платона к проблеме гносеологического восхождения не был чисто академическим или узкоспецифическим – он думал о том, как научить людей сознательно управлять своей жизнью и заботиться о душе и благе государства. Человек, не понимающий, в чем заключается благо, не сможет прожить достойную жизнь, а государственный муж, не понимающий, в чем состоит истинное благо государства, и считающий, что для политики не существует вечных нравственных норм, приведет свое государство к гибели.

Может возникнуть вопрос: содержит ли гносеология Платона, проиллюстрированная Линией познания и аллегорией Пещеры, религиозные аспекты? Всем известно, что неоплатоники придали теории Платона религиозную окраску; более того, христианский писатель, к примеру Псевдо–Дионисий, повествующий о мистическом восхождении видимых существ к их невидимому Источнику (то есть Богу), свет которого столь ярок, что ослепляет и душа погружается в состояние, которое можно назвать ослепительным мраком, вне всякого сомнения, опирается на идеи Платона, подхваченные неоплатониками. Однако из этого вовсе не следует, что сам Платон понимал восхождение по линии познания с точки зрения религии. В любом случае этот сложный вопрос нельзя обсуждать до тех пор, пока не будет рассмотрена онтологическая природа и статус Платоновой Идеи Блага, и даже после этого вряд ли можно будет дать на него ясный и недвусмысленный ответ.

Глава 19

Дата добавления: 2014-10-31