Статистический метод определения суммарной погрешности

Содержанием статистического метода является измерение размера (или другого параметра) деталей анализируемой совокупности, вычисление характеристик распределения, построение практической кривой распределения, анализ кривой и характеристик распределения и выбор на этой основе теоретического закона распределения анализируемой совокупности. Все эти данные позволяют вычислить составляющие суммарной погрешности и всю погрешность.

При статистическом анализе точности необходимо соблюдение следующих требований:

а) для анализа брать детали, изготовленные при стабильных условиях, т. е. одним размерным инструментом до его переточки или при одной наладке станка (между двумя подналадками);

б) число деталей в совокупности должно быть значительным. Чем больше взято деталей для анализа, тем с большей достоверностью будут определены характеристики распределения;

в) измерение деталей должно выполняться инструментом, цена деления которого должна быть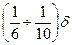, где δ - допуск на измеряемый размер.

Содержание всех этапов статистического метода определения операционной погрешности рассмотрим на примере. На автомате с выдерживанием размеров по настройке была изготовлена партия роликов D = 20_-0,2 в количестве N=100штук. Размеры деталей занесены в таблицу измерений (табл.2). Пользуясь данными таблицы, вычисляем практическое поле рассеивания (размах варьирования, широту распределения):

R=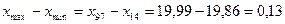мм

Таблица 2- Таблица размеров деталей, мм [7]

19,93 19,87 19,97 19,89 19,95 19,92 19,94 19,89 19,95 19,93

19,97 19,92 19,93 19,86 19,88 19,95 19,88 19,94 19,93 19,94

19,96 19,94 19,92 19,87 19,93 19,89 19,95 19,93 19,94 19,94

19,92 19,96 19,89 19,92 19,94 19,93 19,93 19,94 19,95 19,88

19,97 19,96 19,95 19,88 19,92 19,95 19,89 19,94 19,92 19,95

19,92 19,97 19,95 19,93 19,89 19,92 19,95 19,88 19,91 19,97

19,91 19,96 19,93 19,91 19,90 19,91 19,92 19,90 19,96 19,90

19,90 19,93 19,97 19,90 19,88 19,91 19,97 19,92 19,91 19,91

19,90 19,89 19,91 19,89 19,97 19,91 19,89 19,91 19,92 19,91

19,90 19,88 19,90 19,92 19,90 19,98 19,91 19,99 19,91 19,92

Для удобства обработки статистических данных и построения кривой распределения величину размаха разделяют на разряды (интервалы). Число разрядов kдолжно быть увязано с количеством деталей в совокупности: при N=50—100 шт. k=5—7, при N>100 k=7—11. Кроме того, число разрядов должно быть таким, чтобы цена разряда c=R/k былабольше цены деления мерительного инструмента. Выполнение этого требования необходимо для того, чтобы уменьшить влияние погрешностей измерений. Примем для нашего примера k=7. Тогда расчетная цена разряда будет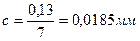. Примем с=0,02 мм. Заметим, что округление цены разряда должно быть минимальным и допустимо в большую сторону.

Для решения поставленной задачи необходимо вычислить главные характеристики распределения: статистический центр группирования или среднее арифметическое значение размера для совокупности х_ср и среднее квадратичное отклонение σ по уравнениям:

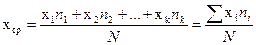(3.16)

σ =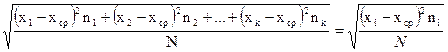 (3.17)

В этих уравнениях x_i, x_2…x_k — значения представителей разрядов;

n₁, n₂,... n_k — количество деталей (частота) в разряде. Важным является выбор границ между разрядами: они должны проходить не по измеренным значениям размеров, а между ними. Примем граничными значения x_i19,855, 19,875 и т. д.

Результаты расчетов x_cр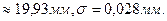

Рис.16 Практическая 1 и теоретическая 2 кривые распределения

Следующим этапом является построение практической кривой распределения. Она строится в координатах x_i, n_i. Масштабы по осям выбираются произвольные, удобные для построения. Практи­ческая кривая для нашего примера приведена на рис.16 (ломаная линия). При ее построении приняты масштабы: по оси x_i0,01 мм соответствует 10 мм; по оси n_i1 деталь — 2 мм. Построение кривой выполняется обычным путем: для всех значений х_i(19,87, 19,89 и т. д.) откладываются по вертикали в масштабе соответствующие им значения n_i. Полученные точки соединяются отрезками прямой.

Практическая кривая служит для первой приближенной оценки точности процесса, оценки «чистоты» эксперимента и правильности обработки результатов измерений и решения вопроса о выборе те­оретического закона для характеристики данного распределения. Приближенной же потому, что форма практической кривой распределения зависит не только от объективных причин — характера распределения размеров, но и от случайных — числа интервалов или разрядов k, количества принятых для анализа деталей N. В связи с этим, для объективной оценки точности обработки прак­тические кривые необходимо заменить теоретическими кривыми, изображающими вполне определенные законы распределения, за­даваемые математическими уравнениями.

В разд. 3.4.1 был сделан краткий обзор теоретических законов распределения. Возникает вопрос — какой из них следует исполь­зовать для характеристики распределения размеров обследован­ной партии деталей. Правильно будет при решении этого вопроса исходить из анализа условий обработки партии деталей и характеpa действия причин, обусловивших распределение погрешностей. Многочисленные исследования показали, что при механической об­работке деталей на металлорежущих станках по способу автомати­ческого достижения заданных размеров (по настройке, с использо­ванием мерного режущего инструмента) распределение размеров подчиняется (в достаточной мере соответствует) закону нормально­го распределения. На этом основании примем этот закон для ха­рактеристики рассматриваемого в примере распределения разме­ров роликов D=20_-0,2.

Для распределения по этому закону, как отмечалось выше, при­нимают шестисигмовое поле рассеивания, т. е. принимают ω_ρ = 6σ. Для нашего примера: ω_ρ = 6σ = 6·0,028 = 0,168 мм. Следует обратить внимание на то, что теоретическая величина поля рассеивания оказалась значительно больше практического поля (размаха варьирования): 0,168>0,13 мм. Объясняется это тем, что размах варьиро­вания R = 0,13 мм характеризует точность конкретной партии с ко­личеством N=100 штук деталей. Теоретическое же поле рассеива­ния позволяет дать оценку метода обработки, прогнозировать точ­ность обработки сколько угодно большого числа деталей. Можно с большой достоверностью утверждать, что если по данному методу на данном станке, при поддержании на принятом уровне всех ос­тальных условий, обрабатывать детали в неограниченном количест­ве и неограниченное время, то поле рассеивания будет составлять

ω_p=0,168мм.

Теперь построим кривую нормального распределения, причем для возможности сопоставления и анализа будем строить ее совме­щенной с эмпирической кривой и согласуем их масштабы. По оси х для эмпирической кривой было принято 0,01→10 мм. Тогда для теоретической кривой σ = 0,028→28 мм. Для увязки масштабов по оси ординат из условия равенства площадей под кривыми используем уравнение

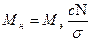, (3.18)

где М_н и М_э — масштабы соответственно для кривой нормального распределения и эмпирической кривой; с — цена разряда (ранее было принято с = 0,02 мм); Ν — число деталей в совокупности (Ν= 100). Для нашего примера

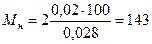. (3.19)

При построении кривой нормального распределения сначала откла­дывается ее ось, соответствующая x_cp= 19,93 мм. Это значение xпринимается за начало отсчета точек на оси xв долях σ. По оси у откладываются ординаты кривой нормального распределения. Для их определения нет необходимости производить каждый раз вычисления по уравнению кривой у=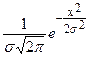, можно воспользоваться табличными значениями этой функции.

Сравнение эмпирической и нормальной кривых по степени совпадения их формы, площадей и положения, позволяет судить о характере влияния факторов процесса на погрешность изготовления детали.

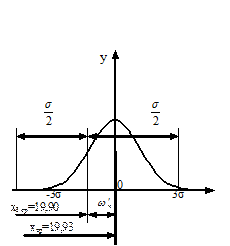
Выше была определена одна составляющая суммарной погрешности — ω_р=6σ. Перейдем теперь к определению другой составляющей — ω_п, учитывающей влияние постоянных систематических погрешностей. На рис.17 изображено поле допуска на размер обрабатываемых в примере деталей δ=0,2 мм с координатой его середины х_δср = 19,90 мм. В этом поле расположена в масштабе кривая нормального распределения для нашего эксперимента с координатой середины поля рассеивания х_ср = 19,93. Из схемы и сопоставления х_δср и х_срследует, что ось кривой распределения смещена с середины поля допуска за счет влияния постоянных систематических погрешностей на величину:

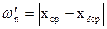(3.20)

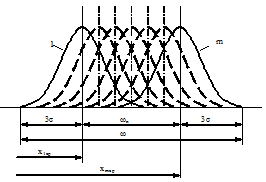
Для нашего примера ω_п' = 19,93—19,90 = 0,03 мм. Величина ω_п' характеризует направление и степень влияния постоянных систематических факторов, действовавших (имевших место) при обработке анализируемой партии деталей. Обычно для производственных и научных целей основным является определение точностных характеристик не отдельной партии деталей, а метода обработки, т.е. генеральной совокупности деталей. Генеральная совокупность (склад) включает детали многих партий, изготовляемых в разное время, на разных станках и при разных наладках (или разными мерными инструментами). Если для каждой партии вычислить ха­рактеристики распределения и для всех партий построить кривые распределения — получилась бы не одна, а семейство кривых, расположенных как показано на рис. 18.

По этой схеме становится очевидной структура уравнения (3.15): ω=ω_п+ω_р= ω_п+6σ.

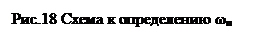
При этом величина постоянной составляющей может быть, определена по формуле:

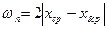(3.21)

Используем это уравнение для оценки влияния постоянных систематических факторов по данным нашего примера: 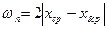= =2(19,93—19,90) =0,06 мм. Тогда, в соответствии с уравнением (3.15) суммарная погрешность использованного в примере метода обработки будет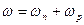= 0,06 + 0,168 = 0,228 мм. Вычисленная величина ω превышает допуск на выполняемый размер: 0,228>0,20 мм. Следовательно, хотя в экспериментальной партии все N=100 штук деталей имели размеры в пределах допуска (см. табл.2), при использовании этого метода в последующем, при обработке неограниченно большого количества деталей, возможен выход размеров части деталей за пределы поля допуска.

Рассмотрим теперь использование результатов статистического анализа и метода кривых распределения.

По форме эмпирической кривой распределения можно судить о доминирующем закономерно изменяющемся факторе. Например, кривая со скругленной, плоской вершиной будет свидетельствовать о большом влиянии размерного износа инструмента. Получение двухвершинной кривой для деталей, обработанных при одной настройке (одним мерным инструментом) указывает на то, что в какой то момент обработки в действие включился непредвиденный постоянный фактор — сбилось положение инструмента и т. п. По положению центра группирования в поле допуска, т. е. по величине 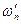можно судить о качестве настройки станка или о соответствии размера мерного инструмента заданному значению.

По соотношению поля рассеивания ω_р = 6σ и поля допуска σможно судить, о возможности обработки деталей по настройке и о до­пуске на настройку.

В тех случаях, когда суммарная погрешность оказывается больше допуска на выполняемый размер, т. е. при ω=ω_п+ω_р>δ, метод кривых распределения позволяет определить вероятный процент годных деталей или вероятный процент брака.

4.Поверхностный слой деталей

Дата добавления: 2014-10-31