
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Уравнения Максвелла
|
|
|
|
Полная система уравнений Максвелла для электромагнитного поля имеет вид:


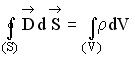

Следующая система уравнений:


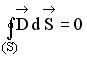

справедлива для переменного электромагнитного поля …
1) при наличии заряженных тел и в отсутствие токов проводимости
2) при наличии заряженных тел и токов проводимости
3) при наличии токов проводимости и в отсутствие заряженных тел
4) в отсутствие заряженных тел и токов проводимости
| Система уравнений Максвелла (для переменных полей) | ||
| № | Уравнение | Что характеризует |

| Это уравнение показывает, что источниками электрического поля могут быть не только электрические заряды, но и изменяющиеся во времени магнитные поля | |

| Это уравнение показывает, что магнитные поля могут возбуждаться либо движущимися зарядами (электрическими токами), либо переменными электрическими полями.
В скобках правой части уравнения указана плотность полного тока, равного сумме токов проводимости j и смещения  . .
| |
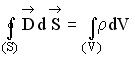
| Это уравнение выражает теорему Гаусса для электростатического поля: поток вектора напряженности электростатического поля сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на  . Если правая часть уравнения равна нулю, т.е. . Если правая часть уравнения равна нулю, т.е.  , то уравнение , то уравнение 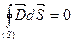 означает об отсутствии зарядов (заряженных тел) внутри замкнутой поверхности. означает об отсутствии зарядов (заряженных тел) внутри замкнутой поверхности.
| |

| Это уравнение показывает на отсутствие в природе магнитных зарядов. | |
Ответ: вариант 3.
Приведенная система уравнений Максвелла справедлива при наличии токов проводимости и в отсутствие заряженных тел. На наличие токов проводимости в системе показывает уравнение 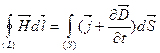 , и отсутствие заряженных тел обусловлено уравнением , и отсутствие заряженных тел обусловлено уравнением 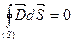 . . 
|
Полная система уравнений Максвелла для электромагнитного поля имеет вид:


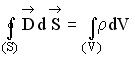

Следующая система уравнений:


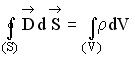

1) справедлива для переменного электромагнитного поля …
2) при наличии заряженных тел и токов проводимости
3) при наличии токов проводимости и в отсутствие заряженных тел
4) при наличии заряженных тел и в отсутствие токов проводимости
5) в отсутствие заряженных тел и токов проводимости
Решение:
В приведенной системе уравнений, в частности  , отсутствует ток проводимости j(см. предыдущее задание).
Ответ: вариант 4. , отсутствует ток проводимости j(см. предыдущее задание).
Ответ: вариант 4.
|
Полная система уравнений Максвелла для электромагнитного поля имеет вид:


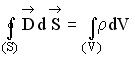

Следующая система уравнений:
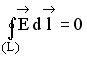

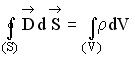

справедлива для …
1) стационарного электромагнитного поля в отсутствие заряженных тел
2) стационарных электрических и магнитных полей
3) стационарного электромагнитного поля в отсутствие токов проводимости
4) переменного электромагнитного поля при наличии заряженных тел и токов проводимости
Система уравнений Максвелла
(для стационарных полей  ) )
| ||
| № | Уравнение | Что характеризует |
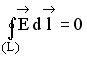
| Это уравнение показывает, что источниками электрического поля в данном случае являются только электрические заряды. Правая часть уравнения  , т.к. , т.к. 
| |

| Это уравнение показывает, что магнитные поля могут возбуждаться в данном случае только движущимися зарядами (токами проводимости). Ток смещения  ,т.к. ,т.к. . .
| |
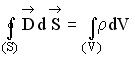
| Это уравнение выражает теорему Гаусса для электростатического поля: поток вектора напряженности электростатического поля сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на  . Если правая часть уравнения равна нулю, т.е. . Если правая часть уравнения равна нулю, т.е.  , то уравнение , то уравнение 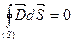 означает об отсутствии зарядов (заряженных тел) внутри замкнутой поверхности. означает об отсутствии зарядов (заряженных тел) внутри замкнутой поверхности.
| |

| Это уравнение показывает на отсутствие в природе магнитных зарядов. | |
| Ответ: вариант 2. Отметим, что последние два уравнения Максвелла при переходе из стационарных полей в переменные, и наоборот, не изменяются. |
Уравнение Максвелла, описывающее отсутствие в природе магнитных зарядов, имеет вид...
1) 
2) 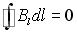
3) 
4) 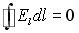
Решение:
Уравнение Максвелла, описывающее отсутствие в природе магнитных зарядов, имеет вид...
 Ответ: вариант 3.
Ответ: вариант 3.
|
|
|
|
|
|
Дата добавления: 2014-10-31; Просмотров: 39424; Нарушение авторских прав?; Мы поможем в написании вашей работы!