Допуски формы и расположения поверхностей

Для обеспечения работоспособности детали в процессе эксплуатации машины или механизма наряду с выполнением размеров детали по чертежу необходимо обеспечить при изготовлении требуемую форму её поверхностей (плоскость, цилиндр, конус и т.п.), а также правильное взаимное расположение поверхностей (параллельность, перпендикулярность, соосность и т.д.). Погрешности формы и расположения поверхностей возникают при механической обработке деталей вследствие упругих деформаций металлорежущего оборудования, инструмента и обрабатываемых деталей, неоднородности материала заготовок деталей и других причин.

Допуски формы и расположения поверхностей указывают на чертежах условными обозначениями в соответствии с ГОСТ 2.308-79. Эти обозначения состоят из графического символа, обозначающего вид допуска (табл. 7.4), числового значения допуска в миллиметрах и буквенного обозначения базы или поверхности, с которой связан допуск расположения.

Допуски формы и допуски расположения поверхностей после их определения округляют до ближайшего числа (мкм) из ряда предпочтительных:

	1,2	1,6		2,5

Таблица 7.4

Знаки условного обозначения допусков формы и расположения поверхностей

На чертежах условное обозначение этих допусков указывают в прямоугольных рамках (рис. 7.4). Рамку знака располагают горизонтально. В необходимых случаях допускается вертикальное расположение рамки.

Рис. 7.4

Разрешается допуски формы и расположения поверхностей указывать текстом в технических требованиях чертежа детали, если отсутствует условный знак допуска.

С элементом детали, к которому относится этот допуск, рамку условного обозначения соединяют сплошной тонкой линией, оканчивающейся стрелкой, направленной на этот элемент (цилиндрическая поверхность, торец, рабочая поверхность шпоночного паза и т.д.).

Базы обозначают зачернённым равносторонним треугольником, высота которого равна высоте размерных чисел. Если базой является поверхность (посадочное отверстие детали, цапфа вала и т.д.), то основание треугольника располагают на видимой контурной линии или на её продолжении на некотором расстоянии от размерной линии. Если же базой является ось (или плоскость) симметрии, то основание треугольника располагают непосредственно под стрелкой размерной линии (рис. 7.5).

Вал и вал-шестерня. Чаще всего базой измерения для этих деталей является общая ось посадочных поверхностей для подшипников качения. Эта ось обозначена на рис. 7.6 буквами АВ.

Рис. 7.5

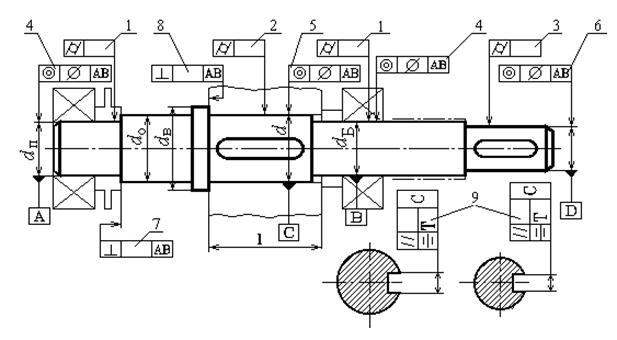
Рис. 7.6

На этом же рисунке приведены обозначения основных диаметров вала (d п, d о, d Би d), а в рамках − условные обозначения допусков формы и расположения и номера позиций, в соответствии с которыми по табл. 7.5 определяют числовые значения этих допусков.

Пример выполнения рабочего чертежа вала приведен на рис.7.7.

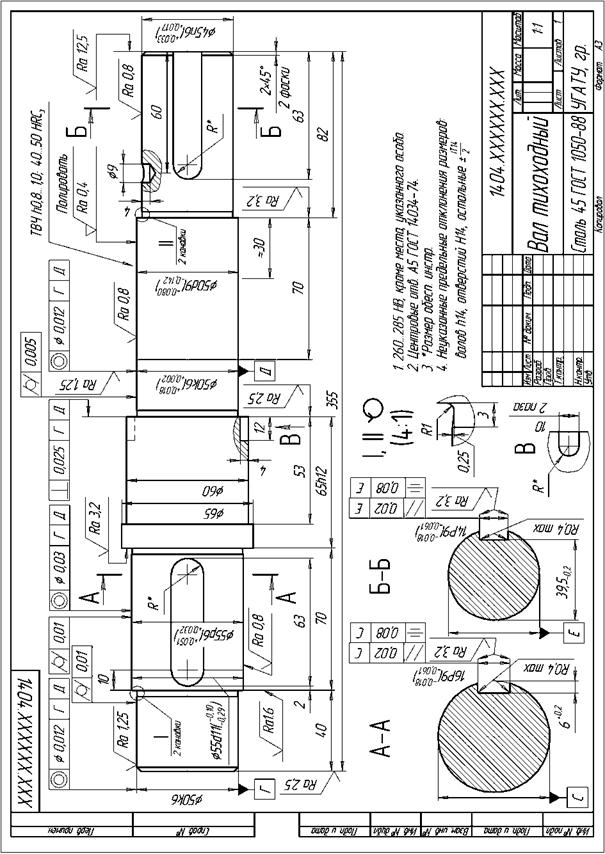
Рис. 7.7

Таблица 7.5

Допуски формы и расположения поверхностей

Позиция	Допуск
1, 2, 3	= 0.5 t, где t − допуск размера поверхности
	TØ на диаметре dn по табл. 7.6, в зависимости от типа подшипника качения.
	TØ на диаметре d по табл. 7.7 Степень точности допуска соосности по табл. 7.8
	TØ = 60 /n мм только для n 1000 об/мин
	Т Ö на диаметре d опо табл. 7.9. Степень точности допуска при базировании подшипников: шариковых − 8, роликовых – 7.
	Т Ö на диаметре dВ при l / d < 0,7 по табл. 7.9 при степени точности допуска перпендикулярности для зубчатых колёс степеней точности по нормам контакта, которую назначают следующим образом: для шестой − 5; для седьмой и восьмой − 6; для девятой – 7.
	Т Õ = 0,5 ∙ t шп, T Ù = 2 ∙ t шп, где t шп− допуск ширины шпоночного паза

Таблица 7.6

Допуск соосности поверхности цапфы вала длиной В = 10 мм

Тип подшипника	TØ, мкм
1. 2. 3. 4. 5.	Радиальный шариковый однорядный Радиально-упорный шариковый однорядный Радиальный с короткими цилиндрическими роликами Радиально-упорный конический роликовый однорядный Радиальный шариковый и роликовый двухрядный сферический
	Примечание: при длине В (мм) посадочного места подшипника на валу, отличного от В1 = 10 мм, табличное значение допуска соосности следует умножить на 0,1 В1.

Таблица 7.7

Допуск соосности поверхности вала

Интервалы диа- метров вала, мм	Степень точности допуска соосности
от	до	Допуск соосности, мкм

Таблица 7.8

Степень точности допуска соосности в зависимости
от кинематической точности зубчатой передачи

Степень кинема- тической точнос- ти передачи	Диаметр делительной окружности колеса, мм
от 50 до 125	от 125 до 280
Степень точности допуска соосности

Зубчатое колесо. На рис. 7.8 показаны несколько зубчатых колёс и условные обозначения баз и допусков формы и расположения поверхностей.

В соответствии с позициями, приведёнными на этом рисунке, в табл. 7.10 даны указания для определения допусков и расположения поверхностей.

Назначение каждого из допусков формы и расположения поверхностей зубчатого колеса следующее:

- в позиции 1 – допуск цилиндрической посадочной поверхности колеса назначают, чтобы ограничить концентрацию напряжений на посадочной поверхности;

Таблица 7.9

Степени точности допусков параллельности, перпендикулярности

Интервалы диаметров, мм	Степень точности допусков параллельности, перпендикулярности
Допуски параллельности, перпендикулярности
от 16 до 25 от 25 до 40 от 40 до 63 от 63 до 100 от 100 до 160

Таблица 7.10

Допуски формы и расположения поверхностей

Позиция	Допуск
	= 0,5 t, где t - допуск размера отверстия d.
	T на диаметре d ст рассчитывают только при l/d 0,7 по таблице 7.9. Степень точности допуска при базировании подшипников: шариковых – 8, роликовых – 7.
	T// на диаметре d ст рассчитывают только при l/d < 0,7 по таблице 7.9. Степень точности допуска при базировании подшипников: шариковых – 7, роликовых – 6.
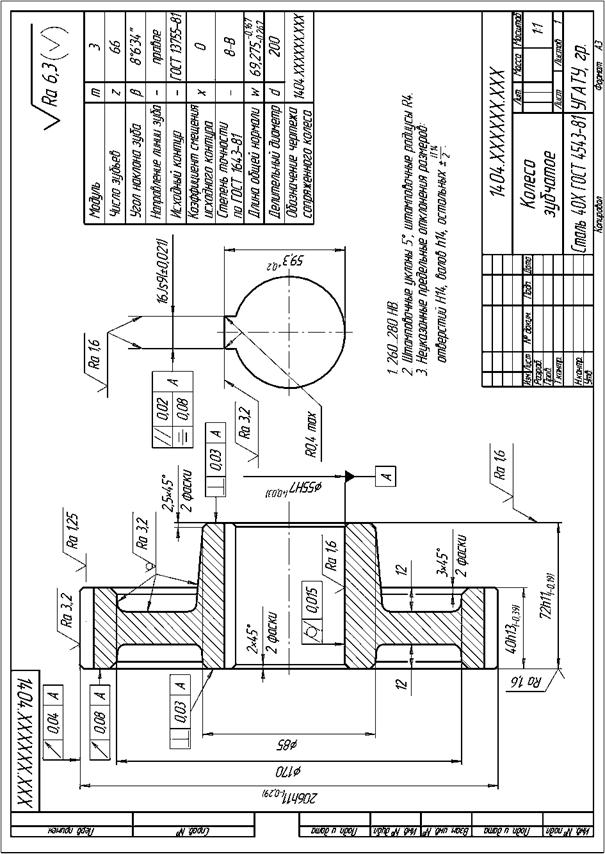
	T//= 0,5 t шп; Т 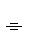= 2 t шп, где t шп- допуск ширины шпоночного паза

Рис.7.8

- в позиции 2 – допуск перпендикулярности торца ступицы колеса задают, чтобы создать точную базу для подшипника качения и уменьшить перекос колец подшипников;

- в позиции 3 – допуск параллельности торцов ступицы для узких колес (l / d < 0,7) задают по тем же соображениям, что и допуск перпендикулярности торца ступицы. Если у колеса нет выточки, следовательно, нет и размера d ст, то допуск параллельности торцов ступицы относится к условному диаметру, равному 1,5…2 размерам посадочного отверстия. Тогда в рамке условного обозначения приводят значение допуска параллельности и условный диаметр измерения, например, для условного диаметра 50 мм при допуске параллельности 0,016 мм.

Если торцы ступицы не участвуют в базировании подшипников, то допуски по позициям 2 и 3 не назначают.

Пример выполнения рабочего чертежа зубчатого колеса приведен на рис.7.9.

Рис. 7.9

Дата добавления: 2014-10-31