Эквивалентные автоматы

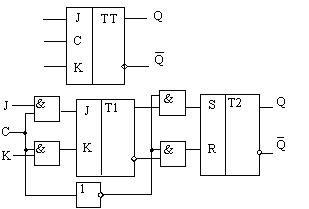
Двухступенчатый триггер

Два автомата S_a и S_b с одинаковыми входными и выходными алфавитами называются эквивалентными. Для любого автомата Мили существует эквивалентный ему автомат Мура, и, обратно, для любого автомата Мура существует эквивалентный ему автомат Мили.

Рассмотрим алгоритм перехода от произвольного конечного автомата Мили к эквивалентному ему автомату Мура.

Пусть дан конечный автомат Мили S_a={A_a,X_a,Y_a,d_a,l_a}, имеющий множество состояний A_a={a₀,a₁,…,a_i,…,a_n}, множество входных и выходных сигналов
X_a={x₁,x₂,…,x_j,…,x_m} и Y={y₁,y₂,…,y_g,…,y_k}, а также функции переходов d_a(a,x) и выходов l_a(a,x).

Требуется построить эквивалентный ему автомат Мура S_b={A_b,X_b,Y_b,d_b,l_b}, у которого X_b=X_a, Y_b=Y_a, так как множества входных и выходных сигналов у эквивалентных автоматов должны совпадать.

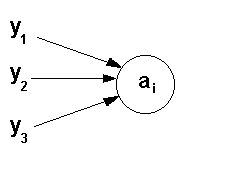
Для определения множества состояний A_b автомата Мура образуем всевозможные пары вида (a_i,y_g), где y_g – выходной сигнал, приписанный к дуге, входящей в состояние a_i. Например, для вершины a_i имеем пары (a_i,y₁), (a_i,y₂), (a_i,y₃).

Если такие пары мы образуем для всех вершин, то получим множество пар, которое является множеством состояний автомата Мура:

A_b={(a₀,y₁), (a₀,y₂),…,(a_n,y_k)}={b₁,b₂,…,b_n}, где b_l=(a_i,y_g).

Функции выходов l_b и переходов d_b определим следующим образом. Каждому состоянию автомата Мура, представляющему собой пару вида (a_i,y_g) поставим в соответствие выходной сигнал y_g, то есть функция выходов равна y_g=l_b[(a_i,y_g)] = l_b[b_l]. Если в автомате Мили S_a был переход
d_a(a_i,x_j)=a_s и при этом выдавался выходной сигнал l_a(a_i,x_j)=y_p, то в эквивалентном автомате Мура будет переход из множества состояний (a_i,y_g), где g принадлежит G, G – множество номеров выходных сигналов, приписанных к входящей a_i дуге, в состояние (a_s,y_p) под действием входного сигнала x_j.

Автомат Мили (фрагмент)

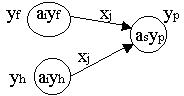
Автомат Мура эквивалентный автомату Мили

Автомат Мили имеет два состояния, а автомат Мура три: (a_i,y_f), (a_i,y_h), (a_i,y_p). Если автомат Мили был в состоянии a_i и пришел входной сигнал x_j, то должен выработаться выходной сигнал y_p. Поэтому в автомате Мура из состояний, порождаемых a_i, то есть из состояний (a_i,y_f) и (a_i,y_h) при поступлении x_j переход должен идти в состояние, отмеченное выходным сигналом y_p, то есть в (a_s, y_p). В качестве начального состояния автомата Мура можно взять любое состояние из множества (a₀, y_r).

Дата добавления: 2014-10-31