
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Полиномиальные счетчики
Счетчик Джонсона
Кодовое кольцо.
Счетчик на кольцевых сдвигающих регистрах
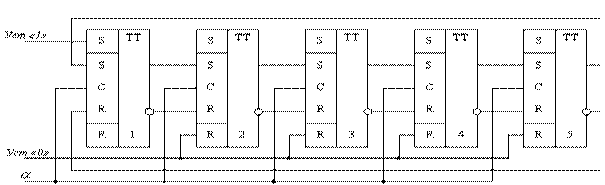
Такой счетчик имеет 5 состояний:
10000 – исходное состояние, затем: 01000, 00100, 00010, 00001,
10000 – вернулись в исходное состояние
Если в приведенной схеме счетчика на кольцевом регистре организовать одну перекрестную связь, т.е. прямой выход последнего триггера соединить со входом R первого триггера, а обратный выход – со входом S, то получится счетчик на регистре с перекрестными связями или счетчик Джонсона. Такой счетчик будет иметь число состояний в два раза больше, чем число разрядов, т.е. k=2n. В нашем примере это состояния: 10000, 11000, 11100, 11110, 11111, 01111, 00111, 00011, 00001, 00000, 10000 и т.д. Т.е. пятиразрядный счетчик имеет коэффициент пересчета, равный десяти. Путем исключения из схемы одного «избыточного» состояния, за счет введения элемента И, можно сделать счетчик Джонсона и с нечетным коэффициентом пересчета k=2n-1. Например, счетчик Джонсона с k =9 на D -триггерах имеет вид:
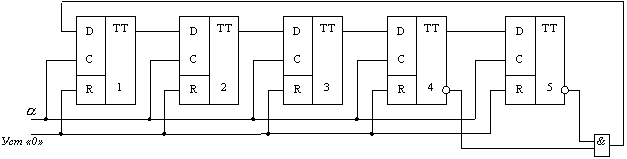
00000 – исходное состояние, затем 10000, 1100, 11100, 11110, 01111, 00111, 00011, 00001, 00000 – вернулись в исходное состояние, состояние 11111 исключено
Полиномиальные счётчики строятся на основе n -разрядного регистра сдвига с линейными обратными связями (с сумматорами по модулю два в цепи обратной связи).
В качестве примера рассмотрим схему счётчика при n = 4:
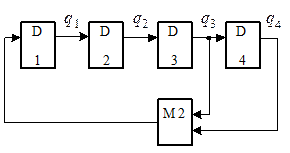
Последовательность состояний регистра сдвига представлена на рисунке (состояние 0 0 0 0 запрещено).
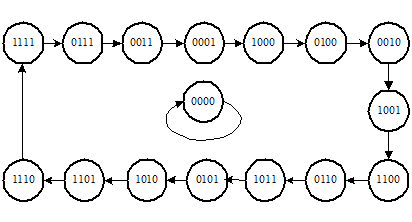
Работа схемы описывается с помощью квадратной матрицы С, связывающей данное 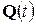 и последующее
и последующее 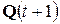 состояния. Для нее состояния триггеров q 1, q 2, q 3и q 4 в момент времени (t+ 1) определятся следующим образом:
состояния. Для нее состояния триггеров q 1, q 2, q 3и q 4 в момент времени (t+ 1) определятся следующим образом:
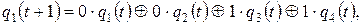
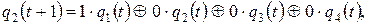
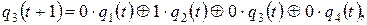
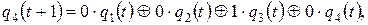
или в матричной форме
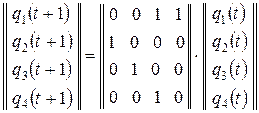
или 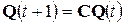 ,
,
где
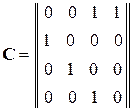 .
.
Первая строка в матрице C определяется видом обратной связи регистра сдвига, остальные единичные элементы матрицы определяют операцию сдвига содержимого регистра.
Периодические свойства последовательностей на выходах счетчика определяются характеристическим многочленом 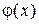 , который является определителем матрицы
, который является определителем матрицы 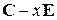 (Е – единичная матрица).
(Е – единичная матрица).
Если многочлен 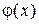 неприводим и примитивен, то счетчик будет формировать последовательность максимальной длины или М- последовательность. Для данного примера характеристический многочлен j (х) неприводим, примитивен и имеет следующий вид:
неприводим и примитивен, то счетчик будет формировать последовательность максимальной длины или М- последовательность. Для данного примера характеристический многочлен j (х) неприводим, примитивен и имеет следующий вид: 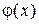 = x 4
= x 4 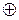 x
x 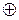 1.
1.
Вероятности появления символа 1 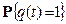 и символа 0
и символа 0 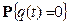 для М-последовательности определяются следующим образом:
для М-последовательности определяются следующим образом:
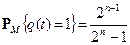 ,
, 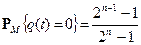 .
.
Известен оригинальный метод построения счетчика на регистре с многошаговым (s -шаговым) сдвигом за один рабочий такт (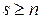 ). Запишем следующие соотношения:
). Запишем следующие соотношения:
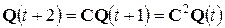 ,
, 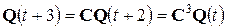 и т.д.
и т.д.
Пусть s = 2. Тогда матрица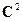 будет имеет вид:
будет имеет вид:
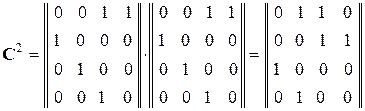 .
.
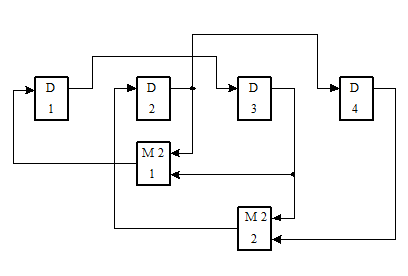
По матрице  построим схему счетчика:
построим схему счетчика:
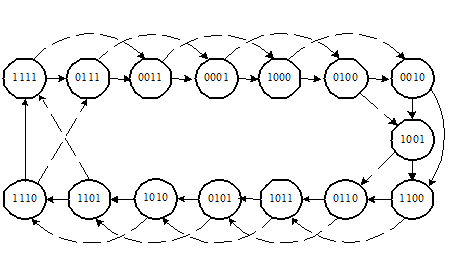
Последовательность состояний регистра сдвига при s = 2 (пунктирные линии) и при s = 1 (сплошные линии) показаны на рисунке.
Как видно из рисунка, счетчик также формирует М-последовательность. Возьмем s = 3. Матрица функционирования счетчика в этом случае имеет вид:
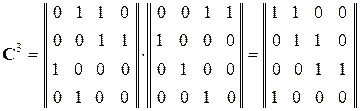 .
.
Рассмотрим схему счетчика при s = 3:
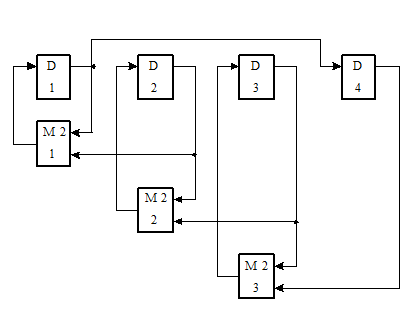
В данном случае D-триггер и сумматор по модулю два в его обратной связи представляют собой T-триггер. Следовательно, эту схему можно преобразовать следующим образом, т.е. она может быть построена только на D- и T-триггерах, соединенных в кольцо.
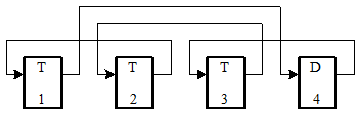

Здесь необходимо отметить, что для того, чтобы каждый выходной разряд счетчика также формировал последовательности максимальной длины, необходимо, чтобы число шагов s и период последовательности M были взаимно простыми числами, т.е. (M, s) = 1. Поскольку в данном примере это условие не выполняется, диаграмма последовательности состояний регистра разбивается на несколько периодов меньшей длины:
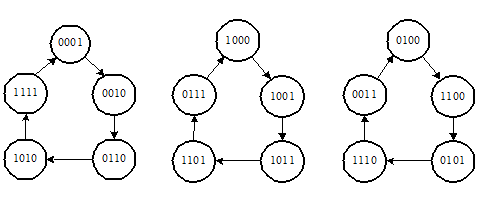
Пусть s = 4. Матрица в этом случае имеет вид:
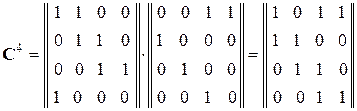 .
.
Схема счетчика приведена на рисунке.
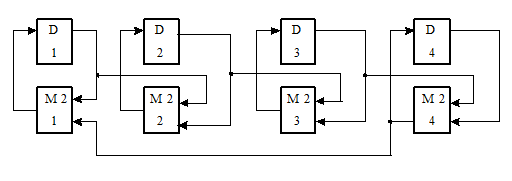
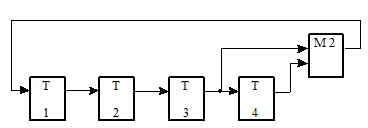
Эта схема может быть построена только на Т -триггерах и одном сумматоре по модулю два:
В общем случае схема полиномиального счетчика на основе n -разрядного регистра сдвига с линейными обратными связями, представлена на рисунке.
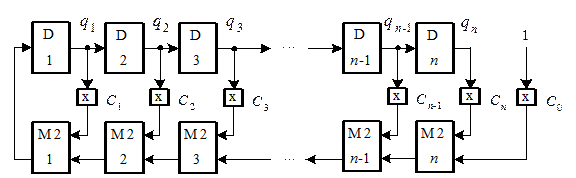
Если коэффициент Ci = 1, то выход i-го триггера подается на вход сумматора по модулю 2, если же Ci =0, то – не подается. В соответствии с коэффициентами многочлена однозначно определяется структура обратной связи регистра сдвига. Есть таблица всех неприводимых многочленов, из которой находят многочлены, представленые в 8-ричной форме.
Например, характеристический многочлен 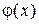 = x 4
= x 4 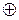 x
x 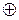 1 в этой таблице будет иметь следующий вид:
1 в этой таблице будет иметь следующий вид:
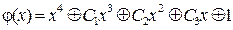 = 1
= 1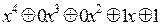 .
.
В двоичном виде этом многочлен запишется как: 10 011, или в 8-ричном виде – 23. По такой записи многочлена однозначно строится схема полиномиального счетчика.
|
|
Дата добавления: 2014-10-31; Просмотров: 1394; Нарушение авторских прав?; Мы поможем в написании вашей работы!