Определение площади палетками

Для определения на плане площадей небольших участков с криволинейными контурами применяют прямолинейные и кри­волинейные палетки. К прямолинейным относят известные и наиболее распространенные квадратные и параллельные палетки.

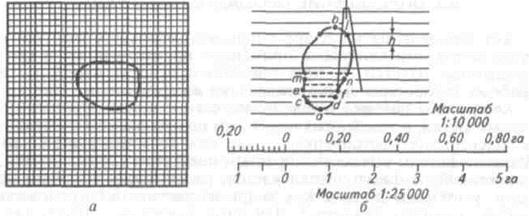
Квадратная палетка представляет сеть взаимно перпендику­лярных линий, проведенных через 1 мм на прозрачном целлулои­де, плексигласе, фотопленке, стекле или восковке (рис.1.1, а). Площадь фигуры вычисляют простым подсчетом клеток палетки, наложенной на фигуру. Доли клеток, рассекаемых контуром на части, учитывают на глаз. Как видно на рисунке 5.2, а, площадь контура занимает 58 клеток¹. Для плана масштаба 1:10 000 пло­щадь клетки со стороной 1 мм равна 10x10= 100 м² = 0,01 га. Сле­довательно, площадь контура равна 0,58 га.

Для упрощения подсчетов проводят утолщенные линии через 0,5 и 1 см, чтобы число клеток можно подсчитать сразу группами (25 и 100 мм²).

Квадратной палеткой не рекомендуют определять площади, большие 2 см² на плане.

Недостаток ее применения помимо того, что площади долей клеток, рассекаемых контуром, приходится оценивать на глаз, со­стоит еще в том, что подсчет числа целых клеток нередко сопро­вождается грубыми ошибками.

Таких недостатков не наблюдается при определении площадей параллельной палеткой, представляющей собой листок прозрачно­го целлулоида, плексигласа или восковки, на котором нанесены параллельные линии, проведенные преимущественно через 2 мм одна от другой (рис.1.1, б).

Площадь контура этой палеткой вычисляют следующим обра­зом. Накладывают ее на контур так, чтобы крайние точки а и b разместились посередине между параллельными линиями палет­ки. Таким образом, весь контур оказывается расчлененным парал­лельными линиями на фигуры, близкие к трапециям с одинако­выми высотами, причем отрезки параллельных линий внутри кон­тура являются средними линиями трапеций. Прерывистыми ли­ниями на рисунке 1.1, б показаны основания этих трапеций. Сумма площадей трапеций, т. е. площадь контура,

P=cdh + efh + mnh +... + klh.

Так как все высоты трапеций равны,

P=h(cd+ef+mn +... + kl)

.

Рис. 1.1 – Определение площади контура квадратной (а) и параллельной (б) палетками

Следовательно, чтобы получить площадь контура, нужно взять сумму средних линий, т. е. сумму отрезков параллельных прямых, проходящих внутри контура, и умножить на расстояние между ними.

Для упрощения определения площади сумму средних линий последовательно набирают в раствор циркуля: сначала берут отрезок cd, затем, не сжимая циркуля, совмещают левую его ножку с точкой /(см. рис. 5.2, б). После этого, не сдвигая правую ножку циркуля с места, увеличивают раствор циркуля, установив левую ножку в точку е. Таким образом, в растворе циркуля получают отрезок, равный cd + ef. Далее левую ножку циркуля устанавливают в точку л, вследствие чего пра­вая ножка встанет от точки п на расстоянии cd + ef После этого, не сдвигая пра­вую ножку с места, раствор циркуля увеличивают, установив левую ножку в точку т, и т.д. Последним отрезом, набираемым в раствор циркуля, будет отрезок к). Набранную в раствор циркуля сумму средних линий определяют по масштабной линейке, и полученную длину умножают на расстояние Л, соответствующее числу метров на местности.

Например, если масштаб плана 1:10 000, h – 20 м и сумма сред­них линий равна 682 м, то площадь контура будет равна 13 640 м², или 1,36 га. Чтобы не выполнять подобных вычислений, для нуж­ного масштаба плана строят специальную шкалу, по которой от­считывают площадь контура, зная сумму средних линий. Рассчи­таем основание шкалы для масштаба 1:10 000. При расстоянии между параллельными линиями 2 мм и при основании шкалы 1 см площадь будет равна 20 • 100 = 2000 м² = 0,20 га. Следовательно, каждому сантиметру шкалы будет соответствовать 0,20 га на мест­ности. Левое основание шкалы делят на 10 частей, как это делают при построении линейного масштаба (см. рис. 1.1, б).

Основанию масштаба 1:25 000, равному 1 см, будет соответство­вать площадь 1,25 га. Такое основание неудобно для определения площадей, поэтому следует рассчитать основание, которому соот­ветствует площадь 1 га. В этом случае длина основания, очевидно, будет равна 0,8 см. Левое основание шкалы также делят на 10 час­тей.

Для масштаба 1:5000 основание принимают 2 см, которое будет соответствовать площади 0,1 га.

После того как сумма средних линий в раствор циркуля набра­на, определяют площадь по шкале так же, как расстояния по ли­нейному масштабу. Палетку и шкалу обычно строит сам исполни­тель. Параллельной палеткой не следует определять площади больше 10 см² на плане.

К криволинейным относят гиперболические палетки, представляющие систе­му гиперболических кривых и применяющиеся для определения площадей про­стейших геометрических фигур. Эти палетки не находят заметного распростране­ния, так как при помощи их нельзя быстро определить площадь участка с криво­линейным контуром.

Дата добавления: 2014-10-31