
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
I. Метод єдиної подібності
|
|
|
|
__ __
Будь-яка філософська система (s) є
або об'єктивно-ідеалістичною (a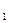 ), або суб'єктивно-ідеалістичною(a
), або суб'єктивно-ідеалістичною(a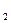 ),
),
або матеріалістичною (b), або дуалістичною (c);
2) розділово-категоричні силогізми – це силогізми, де один із засновків якого – розділове, а інший – категоричне судження.
У розділово-категоричному силогізмі два правильні модуси:
– стверджувально-заперечувальний (modus ponendo tollens):
Структура: S є або A, або B Схема: a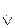 b, а або a
b, а або a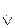 b, b
b, b
‑‑ ‑‑
S є A ~ b ~ a
S не є B
Формули: ((a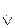 b)
b)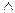 a) →~b; ((a
a) →~b; ((a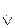 b)
b)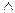 b) →~a – є закони логіки;
b) →~a – є закони логіки;
((a Ú b)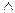 a) →~b; ((a Ú b)
a) →~b; ((a Ú b)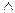 b) →~a – не є закони логіки.
b) →~a – не є закони логіки.
Цей літак (s) або дозвуковий (a), або надзвуковий (b).
Цей літак (s) дозвуковий (a).
Цей літак (s) не надзвуковий (не-b).
– заперечувально-стверджувальний (modus tollendo ponens):
Структура: S є або A, або B
S не є A
S є B
Схеми: a 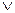 b,~ a a
b,~ a a 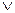 b,~ b a
b,~ b a 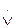 b,~ a a
b,~ a a 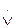 b,~ b
b,~ b
‑ ‑‑‑
b а bа
Формули: ((a 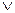 b)
b) 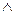 ~ a)→ b; ((a
~ a)→ b; ((a 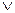 b)
b) 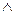 ~ b)→ a – є закони логіки;
~ b)→ a – є закони логіки;
((a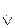 b)
b) 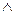 ~ a)→ b; ((a
~ a)→ b; ((a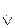 b)
b) 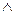 ~ b)→ a – є закони логіки.
~ b)→ a – є закони логіки.
Системи (s) бувають або матеріальні (a), або абстрактні (b).
Ця система (s) не є матеріальною (не-a).
Ця система (s) є абстрактною (b).
Обов'язковою умовою відносно висновків у розділово-категоричному умовиводі є те, що в розділовому засновку мають бути передбачені усі можливі альтернативи, тобто ділення має бути повним.
3) розділово-умовні силогізми – це умовиводи, де один (перший) із засновків є розділовим судженням, а інші засновки є умовними судженнями; кількість інших засновків дорівнює кількості членів розділового судження-засновку.
Структура: S є або A, або B Схема: a Ú b, a→d, b→e
Якщо A, то D d 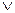 e
e
Якщо B, то E
S є або D, або E
Формула: ((a 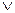 b)
b) 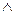 (a→d)
(a→d) 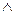 (b→e)) → (d
(b→e)) → (d 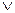 e)
e)
Для отримання знань (s) необхідно
або вчитися в навчальному закладі (a), або вчитися самостійно (b).
Щоб вчитися в навчальному закладі (a), необхідно вступити до нього (d).
Щоб вчитися самостійно (b)
треба самому шукати необхідну інформацію (e).
Для отримання знань (s) треба
або вступити до навчального закладу (d)
або самому шукати необхідну інформацію (e).
2. Індуктивні умовиводи. Принципово інший вид умовиводу – це індуктивний умовивід.
Індуктивний умовивід:
– це метод виробництва загального знання з часткових або одиничних засновків, на відміну від спрямованості думки в дедуктивному умовиводі – від загального до часткового;
– спирається на емпірично спостережувані предмети, які (або їх ознаки) в дедуктивному умовиводі можуть бути присутніми як менший засновок, що не є логічно необхідним;
– дає висновки різного ступеня імовірності, що не заперечує їх логічної правильності, тоді як дедуктивний умовивід визнається логічно правильним тільки у разі демонстративного, тобто логічно необхідного характеру висновку;
– припускає множину суджень-засновків, тобто кількість елементів може бути не визначена точно або бути актуально нескінченою, а дедуктивний умовивід (простий силогізм) завжди є висновок з двох засновків-суджень;
– усі засновки індуктивного умовиводу – рівнозначні, тобто між засновками відсутня відмінність за ступенем загальності (перший засновок, другий, третій і т.д. у будь-якій послідовності), а в дедуктивному умовиводі завжди визначаються більший і менший засновки;
– зв'язок між термінами висновку даний безпосередньо і в кожному засновку, а в дедуктивному умовиводі зв'язок між термінами висновку – S і Р, які є крайніми, не даний ні в одному з засновків, тут зв'язок встановлюється тільки у висновку завдяки відношенню кожного з цих термінів до середнього терміну, присутнього і в одному, і в інших засновках.
Індуктивний умовивід здійснюється за допомогою індукції.
Індукція: в широкому розумінні – це умовивід, в якому думка рухається від знань про одиничне до знань про загальне; у вузькому – це форма правдоподібного умовиводу, в якому на основі знань, відображених у засновках про окремі предмети певної множини, отримують висновок про усю множину (клас) предметів:
S (є) має ознаку Р
S (є) має ознаку Р
S (є) має ознаку Р
...........................................
S (є) має ознаку Р
S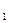 , S
, S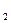 , S
, S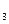 ... S
... S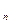 належить класу (
належить класу (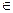 ) К
) К
Імовірно, кожен елемент класу К має ознаку Р (S є Р).
Серед видів індукції виділяють повну, неповну і математичну.
Повна індукція – це такий умовивід, в якому загальний висновок про усі елементи класу предметів робиться на підставі розгляду кожного елементу цього класу, тобто вивчаються усі предмети цього класу, а засновками служать або одиничні, або загальні судження:
Формула: А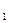 – а
– а
А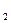 – а
– а
А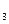 – а
– а
..........
А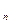 – а
– а
А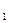 , А
, А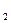 , А
, А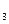 ... А
... А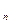 – а (тобто А
– а (тобто А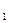 , А
, А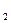 , А
, А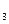 ... А
... А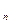 вичерпують клас а).
вичерпують клас а).
‑_
Отже, усі А – а (тобто повна індукція дає достовірні результати, які, однак, не містять нічого нового).
Формула повної індукції в символічній логіці:
Р (х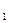 )
)
Р (х 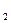 )
)
Р (х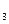 )
)
..........
Р (х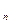 )
)
< х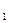 , х
, х 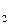 , х
, х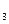 ... х
... х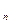 >
> 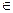 К
К
_‑‑
" х ((х 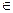 К)→ Р (х))
К)→ Р (х))
Формула читається: «Елементи х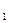 , х
, х 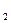 , х
, х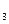 ... х
... х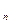 мають ознаку Р. Кінцева множина цих елементів складає клас К. Отже, ознака Р належить усім елементам класу К».
мають ознаку Р. Кінцева множина цих елементів складає клас К. Отже, ознака Р належить усім елементам класу К».
Олексій (А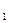 ) вчиться добре з математики (а).
) вчиться добре з математики (а).
Олена (А 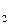 ) вчиться добре з математики (а).
) вчиться добре з математики (а).
Олег (А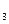 ) вчиться добре з математики (а).
) вчиться добре з математики (а).
...............................................................
і так про кожного із студентів цієї групи (А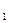 , А
, А 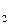 , А
, А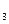 … А
… А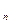 ),
),
що навчаються добре з математики (а).
Усі студенти(А) цієї групи вчаться добре по математиці (а).
Висновки повної індукції мають достовірний характер, оскільки в цьому випадку досліджуються усі предмети певної множини. Якщо засновки такого умовиводу є істинними, то і його висновок теж має бути істинним. Повна індукція використовується тільки при пізнанні закінчених класів. На відміну від дедукції, яка має теж достовірний характер, повна індукція не дає знань про інші предмети, окрім тих, які мисляться в одиничних судженнях-засновках.
Неповна індукція – це умовивід, в якому на підставі повторюваності ознаки у деяких елементів множини (класу) робиться висновок про її приналежність усім елементам:
Формула: А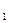 – а
– а
А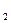 – а
– а
А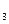 – а
– а
..........
А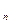 – а
– а
...........
Отже, імовірно, що всі А – а (тобто неповна індукція, навпаки, дає результати, які є новими, але не достовірними, а лише імовірними).
Формула неповної індукції в символічній логіці:
Р (х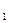 )
)
Р (х 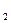 )
)
Р (х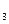 )
)
..........
Р (х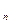 )
)
х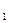 , х
, х 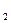 , х
, х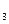 ... х
... х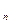 Ì К
Ì К
_‑‑
" х ((х 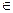 К)→ Р (х))
К)→ Р (х))
Формула неповної індукції відрізняється від повної тим, що множина, або клас, що охоплюється неповною індукцією, є відкритим, внаслідок чого перераховані елементи, що мають фіксовану у засновках і висновку ознаку, складають лише частину або підмножину класу, що зачіпається індукцією.
У цій групі вчиться 20 студентів.
Встановлено, що 18 з них добре склали іспит з історії.
Двоє інших не складали або невідомо, як вони його склали.
На підставі наявної інформації робиться висновок, що
уся група склала іспит добре.
Застосовується, коли, не спостерігаючи усі випадки досліджуваного явища (вони усі невідомі, їх багато, або їх вивчення неможливе), робиться висновок для усіх випадків. Але висновок не є достовірним, тому що, як у наведеному прикладі, не можна стверджувати, що інші студенти, відносно яких немає інформації, теж склали іспит добре. Отже, висновок може бути як істинним, так і неістинним. У той же час, неповна індукція призводить до розширення знання, оскільки ознака, що притаманна відомим явищам, поширюється на область невідомого, емпірично недослідженого. Для підвищення висновку неповної індукції застосовуються спеціальні методи, залежно від яких виділяють три види неповної індукції.
Три види неповної індукції: популярна (або перелічувальна), селективна (від. лат. selectio – вибір, відбір; або індукція через аналіз і відбір фактів) і наукова:
– популярна (перелічувальна) індукція – це індукція, при якій предмети з досліджуваною ознакою перераховуються підряд, у порядку їх появи у сфері чуттєвого сприйняття суб'єкта, або випадковим чином і якщо одна й та ж ознака повторюється у ряді однорідних предметів і відсутній випадок, що суперечить, то робиться загальний (імовірний, а не достовірний) висновок, що ця ознака властива усім предметам цього роду.
Так, довгий час європейці вважали, що лебеді можуть бути тільки білими. Проте це представлення було спростоване, коли в Австралії в 17 ст. були виявлені й чорні лебеді;
– селективна індукція (індукція через аналіз і відбір фактів) – це індукція, де спостереження предметів виключає випадкові висновки, оскільки вивчаються планомірно і цілеспрямовано відібрані, найбільш типові випадки, на основі певної системи критеріїв – кількісний (прикладів спостережуваних предметів повинно бути якомога більше) і якісний (умови фіксації, різноманітність у просторово-часовому і функціональному відношеннях і т.д.).
Наприклад, для отримання репрезентативного, науково обґрунтованого висновку, недоцільно опитувати усю генеральну сукупність, тобто сукупність усіх можливих соціальних об'єктів. Досить правильно зробити вибірку, обмеживши число респондентів з тим, щоб воно забезпечувало помилку висновку, що не перевищує допустимої погрішності;
– наукова індукція – це індукція, в якій на підставі встановлення суттєвих ознак або необхідних (в першу чергу, причинних) зв'язків між предметами класу робиться (достовірний) загальний висновок про усі предмети цього класу.
Наукова індукція припускає використання спеціальних методів, які базуються на поєднанні власне індукції і принципу одноманітності причин і їх наслідків. Наукова індукція названа по іменах розробників її методів – індукція Ф.Бекона-Дж.С.Мілля.
Методи індуктивної логіки (методи встановлення причинних зв'язків) засновані на знанні і використанні загальних рис причинного зв'язку, серед яких необхідно назвати такі:
2) кожне явище світу має причину, яку можна і треба встановити;
2) явище-причина настає в часі раніше, ніж явище-наслідок;
3) після явища-причини неодмінно настає явище-наслідок;
4) за відсутності явища-причини явище-наслідок не настає;
5) зміни в причині призводять до відповідних змін в наслідку.
Основні методи встановлення причинних зв'язків:
Якщо певна обставина постійно передує досліджуваному явищу при зміні усіх інших обставин, то імовірно, що саме вона і є причиною цього явища.
Схема: АВС→а
АDЕ→а
АКМ→а
◊ (А→а), тобто чинники АВС викликають ознаку а; чинники АDЕ викликають ознаку а; чинники АКМ викликають ознаку а; таким чином, імовірно, що А є єдиною причиною ознаки а.
Приклад: При температурі повітря нижче нуля, тобто в мороз (А), вода в рідкому стані, що знаходиться в трьох різних посудинах, – металевій (В), скляній (D) і дерев'яній (К), в різний час доби – ясний день (С), темну ніч (Е) і сутінок (М), перетворюється на лід (а). Загальним для усіх трьох обставин є мороз (А), який при зміні інших обставин (ВС, DЕ, КМ), імовірно, і став причиною перетворення води на лід (а).
ІІ. Метод єдиної відмінності.
Якщо певна обставина є присутньою тоді, коли має місце досліджуване явище, і відсутня тоді, коли це явище відсутнє (а усе інше залишається незмінним), то саме ця обставина і є імовірною причиною досліджуваного явища.
Схема: АВСD→а
ВСD→
◊ (А→а), тобто чинники АВСD викликають ознаку а; чинники ВСD не викликають ознаку а; таким чином, імовірно, що А є єдиною причиною ознаки а.
Приклад: Якщо людина спожила в їжу продукти (ABCD), серед яких був апельсиновий сік (А), який викликав алергічну реакцію (а), оскільки інші продукти були колишніми (BCD), і якщо в наступні дні, коли вона не пила апельсиновий сік, у неї не було алергічних реакцій, а продукти харчування залишалися тими ж (BCD), то, імовірно, апельсиновий сік (А) викликає алергію (а).
|
|
|
|
|
Дата добавления: 2014-10-31; Просмотров: 871; Нарушение авторских прав?; Мы поможем в написании вашей работы!