Информационные характеристики источника дискретных сообщений

Рассмотрим дискретный источник, выдающий последовательность сообщений из некоторого ансамбля возможных сообщений , где , 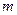- объем алфавита.

Рассмотрим дискретный источник, выдающий последовательность сообщений 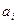из некоторого алфавита.

Среднее количество информации, приходящееся на одно сообщение, выдаваемое дискретным источником, называется энтропией источника:

, .

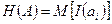Для источника независимых сообщений:

.

Для источника зависимых сообщений вводят понятие условной энтропии, которая характеризует среднее количество информации, которое несет последующий символ сообщения, при условии, что уже известен ряд предыдущих.

,

где - вероятность появления 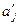при условии, что перед ним появился .

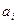Энтропию рассматривают как меру неопределенности в поведении источника. Чем она выше, тем труднее запомнить (записать) сообщение или передать его по каналу связи.

Основные свойства энтропии:

- для дискретных сообщений она – величина вещественная, ограниченная и положительная;

- равна нулю, если с вероятностью 1 всегда выбирается один и тот же символ;

- максимальна, если все символы источника появляются независимо и с одинаковой вероятностью:

;

- энтропия аддитивна, т. е. Если рассматривать последовательность из 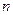сообщений как одно укрупненное сообщение, то энтропия такого источника будет в 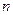раз больше энтропии исходного источника.

Избыточность источника дискретных сообщений.

Количественно оценивается коэффициентом избыточности:

.

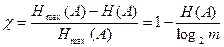Она показывает, какая доля максимально возможной при этом алфавите энтропии не используется источником.

Причины избыточности:

- различные вероятности отдельных сообщений;

- наличие статистических связей между сообщениями.

Устранение избыточности сообщения – это задача эффективного кодирования источников дискретных сообщений.

Производительность источника – среднее количество информации, создаваемой источником в единицу времени. Измеряется в бит/с.

,

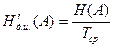где 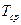- средняя длительность сообщения.

Дата добавления: 2014-10-31