Существенно нелинейный режим работы НЭ

Рассмотрим режим работы, получаемый при сдвиге рабочей точки 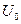влево и увеличении амплитуды возбуждающего напряжения (рисунок 15.4). В данном случае целесообразно применить кусочно-линейную аппроксимацию ВАХ:

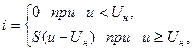
где 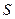- крутизна линейно возрастающего участка ВАХ,

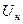- координата его начала.

Форму реакции находим графическим методом. Типичное взаимное расположение ВАХ и сигналов показано на рисунке 16.2.

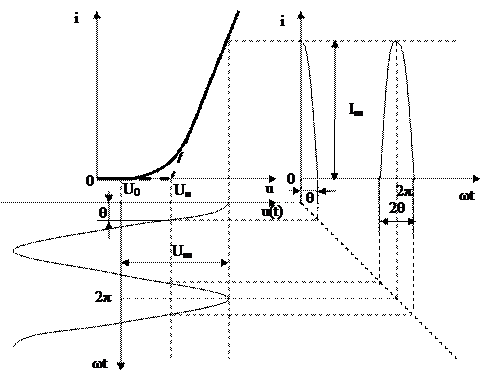
Рисунок 16.2 – Определение формы реакции методом проекций.

Форма реакции имеет вид периодической последовательности косинусоидальных импульсов с отсечкой. Полученные импульсы характеризуются двумя параметрами: высотой 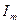и шириной .

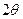Угол, соответствующий половине времени существования импульса, называется углом отсечки 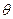. Угол отсечки определяется из равенства:

.

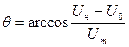В соответствии с формулой при заданной ВАХ (фиксированном 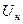) угол отсечки 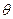регулируется выбором амплитуды 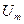величины смещения .

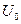Высота (максимальное значение) импульса тока определяется выражением:

.

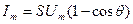Поскольку ток – периодическая функция времени с периодом 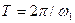, его можно представить в виде ряда Фурье:

.

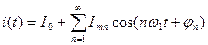Коэффициенты этого ряда являются постоянной составляющей и амплитудами гармоник тока и могут быть вычислены по формулам:

,

,

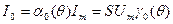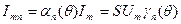где 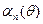- коэффициенты Берга;

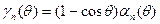- функции Берга.

Для ряда значений 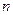коэффициенты и функции Берга табулированы.

Из рассмотрения графиков коэффициентов Берга можно сделать такие заключения: при 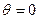ток равен нулю (НЭ заперт на протяжении всего периода); при 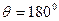отсечка тока отсутствует и режим работы становится линейным; при работе с 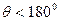отношение амплитуды первой гармоники к постоянной составляющей больше единицы 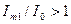и растет с уменьшением 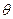; с повышением номера гармоники максимумы амплитуд гармоник перемещаются в область малых значений .

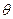Указанные обстоятельства существенно влияют на выбор режима работы НЭ при усилении колебаний, умножении частоты. При умножении частоты для получения наибольшей амплитуды нужной гармоники тока (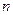-ой) необходимо выбрать оптимальное значение угла отсечки:

.

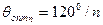Таким образом, вне зависимости от вида аппроксимирующей функции ток через НЭ при гармоническом воздействии представляется суммой постоянной 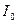и гармонических с амплитудами 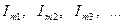и частотами 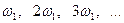, кратными частоте приложенного напряжения, составляющих, т.е. рядом Фурье.

Дата добавления: 2014-10-31