Гармоническая ЧМ

Рассмотрим гармоническую ЧМ (модулирующий сигнал является гармоническим ).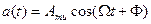

Частота изменяется по закону:

,

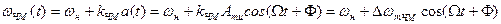где - девиация частоты при ЧМ. Девиация частоты – наибольшее отклонение частоты модулированного сигнала от значения частоты несущей. При ЧМ может принимать значения от единиц герц до сотен мегагерц.

Фаза в момент времени :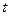

где - индекс частотной модуляции. Является девиацией фазы при ЧМ. Девиация фазы - наибольшее отклонение фазы модулированного сигнала от линейной .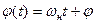

Математическая модель сигнала при гармонической ЧМ:

.

Воспользовавшись тригонометрической формулой: , - преобразуем выражение:

Проведем анализ отдельно для малых и больших индексов модуляции.

В первом случае () имеют место приближенные равенства:

, .

Воспользовавшись тригонометрической формулой: , -

приходим к следующему выражению для ЧМ сигнала:

Рисунок 19.2 – Спектральная диаграмма ЧМ сигнала при М_ЧМ<1.

При малом индексе модуляции – узкополосной ЧМ – амплитудная спектральная диаграмма ЧМ сигнала совпадает по составу (содержит центральную составляющую с частотой несущей 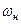, нижнюю и верхнюю боковые составляющие с частотам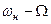и и ) и ширине полосы частот () с АМ сигналом. Отличие заключается в фазовой спектральной диаграмме: фаза нижней боковой составляющей сдвинута на 180⁰.

При малом значении индекса модуляции не будут проявляться преимущества ЧМ (высокая помехозащищенность). Ширина спектра такая же, как и при АМ.

Во втором случае () сложные периодические функции: и 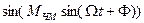- можно разложить в ряд Фурье, а ЧМ сигнал представить в виде суммы гармонических колебаний:

где - функция Бесселя 1-го рода n-го порядка от вещественного аргумента . Табулированы;

n – номер гармонической составляющей: центральная составляющая имеет n=0, боковые – n=1, 2, 3, ….

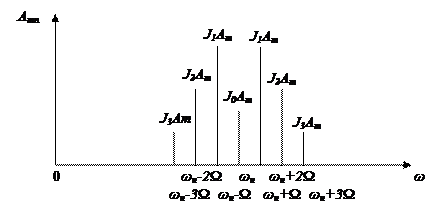
Рисунок 19.3 – Спектр ЧМ сигнала при М_ЧМ=2.

При большом индексе модуляции – широкополосной ЧМ – спектр ЧМ сигнала состоит из бесконечного числа гармоник: из составляющей с частотой несущей 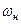, нижней и верхней боковых полос частот, образованных группами составляющих с частотами и 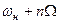. На практике учитывают только те боковые составляющие, амплитуды которых не меньше 5% амплитуды несущей, т.е. для которых . Тогда ширина спектра ЧМ сигнала: .

Данный случай представляет основной практический интерес, поскольку при больших индексах модуляции помехоустойчивость передачи сигнала существенно выше, чем при АМ. Ширина спектра ЧМ сигнала также значительно больше, чем при АМ.

При сложном модулирующем сигнале спектр модулированного сигнала оказывается сложным, содержащим различные комбинационные частоты. Общая полоса частот, занимаемая таким сигналом: , где 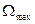- максимальная частота спектра модулирующего сигнала; - индекс модуляции на этой частоте.

Дата добавления: 2014-10-31