Двоичная ЧМн

При двоичной ЧМн (BFSK) символу 1 соответствует отрезок гармонического колебания с частотой 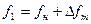, а символу 0 – с частотой 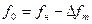, где 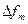- девиация частоты – изменение частоты при передаче 1 (0) относительно ее среднего значения 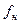. При ЧМн нет пассивной паузы, по этой причине ее называют манипуляцией с активной паузой.

Возможно два случая ЧМн: с разрывом фазы и без разрыва фазы (continuous-phase FSK – CPFSK).

При ЧМн с разрывом фазы назначение каждому двоичному символу своей частоты является произвольным. Полученный сигнал содержит скачки фазы.

t

t

Рисунок 21.3 – Временные сигналов: модулирующего и ЧМн с разрывом фазы.

Наличие разрывов фазы приводит к «размытию» спектра сигнала. Это снижает помехоустойчивость приема и создает помехи другим системам связи. Поэтому при выборе частот следует обеспечить условие плавного (без скачка фазы) перехода от сигнала с частотой 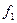к сигналу с частото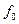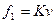й :

и ,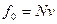

где - число периодов внутри символьного интервала.

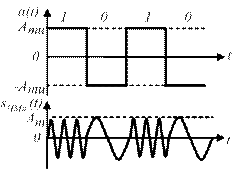
Рисунок 21.4 – Временные диаграммы сигналов: модулирующего и ЧМн

без разрыва фазы.

ЧМн сигнал можно рассматривать как сумму двух отдельных АМн сигналов, один из которых служит только для отображения единиц и имеет несущую частоту 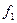, а другой – только нулей и имеет несущую частоту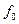. Соответственно, спектр ЧМн сигнала может быть представлен как суперпозиция спектров двух АМн сигналов.

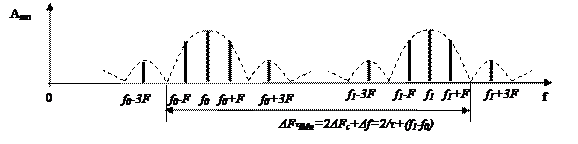
Рисунок 21.5 – Спектральная диаграмма ЧМн сигнала.

Ширина спектра сигнала с двоичной ЧМн определяется выражением:

,

где - разнос частот – расстояние между частотам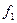и и 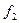. Выбирается таким, чтобы не перекрывались спектры отдельных АМн сигналов;

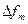- девиация частоты – изменение частоты при передаче 1 (0) относительно ее среднего значения .

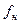ЧМн применяется в радиорелейных и спутниковых системах связи, системах связи с подвижными объектами.

Дата добавления: 2014-10-31