Линейные операторы

Определение. Линейное (векторное) пространство, в котором задано скалярное произведение векторов, удовлетворяющее указанным свойствам с 1 по 4 (рассматриваемым как аксиомы), называется евклидовым пространством.

Евклидово пространство.

Ранее мы определили линейное (векторное) пространство, в котором можно складывать векторы и умножать их на число, ввели понятие размерности и базиса, теперь в данном пространстве введем метрику, т.е. способ измерять длины и углы. Это можно сделать, если ввести понятие скалярного произведения.

Определение. Скалярным произведением двух векторов X = (x₁, x₂,..., x_n) и Y = (y₁, y₂,..., y_n) называется число (Х,У) = x₁y₁ + y₂x₂ +... + y_nx_n (8.1)

Скалярное произведение имеет экономический смысл: если X = (x₁, x₂,..., x_n) – это вектор объемов различных товаров, а Y = (y₁, y₂,..., y_n) – вектор их цен, то скалярное произведение (Х,У) = x₁y₁ + y₂x₂ +... + y_nx_n выражает суммарную стоимость этих товаров.

Скалярное произведение имеет следующие свойства:

1. (X,Y) = (Y,X) – коммутативное свойство;
2. (X,Y + Z) = (X,Y) + (X,Z) – дистрибутивное свойство;
3. ( a X,Y) = a (X,Y) – для любого действительного числа a;
4. (X,X) > 0, если Х – ненулевой вектор; (X,X) = 0, если X – нулевой вектор.

Длиной (нормой) вектора Х в евклидовом пространстве называется корень квадратный из его скалярного квадрата:

(8,2).

Два вектора называются ортогональными, если их скалярное произведение равно нулю. Очевидно, что нулевой вектор ортогонален любому другому вектору. Из определения следует, что если два ненулевых вектора ортогональны, то угол между ними равен p/2 (т.к. cosp/2 = 0)/

Векторы e₁,e₂,... e_n n -мерного евклидова пространства образуют ортонормированный базис, если эти векторы попарно ортогональны и норма каждого из них равна единице, т.е. (e_i,e_j) = 0 при i ¹ j и ç e_i ç= 1 при i = 1,2,...n.

Теорема (без доказательства). Во всяком n -мерном евклидовом пространстве существует ортонормированный базис.

Примером ортонормированного базиса является система n единичных векторов e_i, у которых i – ая компонента равна единице, а остальные компоненты равны нулю: e₁ = (1, 0,... 0), e₂ = (0, 1,..., 0),..., e_n = (0, 0,..., 1).

Рассмотрим два линейных пространства: Rⁿ размерности n и R^m размерности m.

Определение. Если задан закон (правило), по которому каждому вектору Х пространства Rⁿ ставится в соответствие единственный вектор Y пространства R^m, то говорят, что задан оператор (преобразование, отображение) А(Х) и записывают Y = A(X).

Оператор (преобразование) называется линейным, если для любых векторов X и Y пространства Rⁿ и любого числа a выполняются соотношения:

1. A(X+Y) = A(X)+A(Y) – свойство аддитивности оператора;

2. A(aX) = aA(X) – свойство однородности оператора.

Вектор Y = A(X) называется образом вектора Х, а сам вектор Х – прообразом вектора Y.

Если пространства Rⁿ и R^m совпадают, то оператор А отображает пространство Rⁿ в себя. Именно такие операторы мы и будем рассматривать в дальнейшем.

Линейный оператор полностью определяется своими значениями на базисных векторах. В самом деле. пусть в n- мерном линейном пространстве с базисом e₁,e₂,... e_n задано линейное преобразование А. Тогда векторы А(e₁), А(e₂),..., А(e_n) - также векторы этого пространства и их можно представить в виде линейной комбинации векторов базиса:

А(e₁) = a₁₁ e₁ + a₂₁ e₂ +…+ a_n1 e_n

А(e₂) = a₁₂ e₁ + a₂₂ e₂ +…+ a_n2 e_n

……………………………….

А(e_n) = a_n1 e₁ + a_n2 e₂ +…+ a_nn e_n

Тогда таблица (матрица) n´n А = 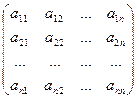называется матрицей линейного преобразования А.

Таким образом, каждому линейному оператору соответствует матрица в данном базисе. И наоборот, каждой матрице размерности n´n соответствует линейный оператор n- мерного пространства.

ГЛАВА 2. МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ.

Дата добавления: 2014-10-31