Линейная зависимость векторов

Определение. Множество векторов с действительными компонентами, в котором определены операции сложения векторов и умножения вектора на число, удовлетворяющие приведенным выше свойствам 1 – 8, называется векторным пространством Rn.

N-мерные векторы и векторные пространства.

Понятие множества является одним из основных в математике.

Определение. Семейство объектов, объединенных по определенному признаку, называется множеством. Объекты, составляющие множество, называются его элементами или точками.

Обычно множества обозначаются большими буквами, а входящие в них элементы – малыми буквами. Элемент x из множества Х - записывается: хÎ Х (х принадлежит Х); если же элемент х не входит в множество Х, то это соответствует записи х Ï Х (х не принадлежит Х). Если все элементы множества Х содержатся в другом множестве Y, то X Ì Y и говорят, что Х является подмножеством множества Y.

Множества всех плоских (2-мерных) или пространственных (3-мерных) векторов, рассмотренных выше, в которых определены операции сложения векторов и умножения вектора на число, являются простейшими примерами векторных пространств. Обобщим понятие вектора для случая n-мерного пространства и дадим определение векторного пространства.

Определение. n-мерным вектором называется упорядоченная совокупность n действительных чисел, записываемых в виде Х = (x₁, x₂,... x_n), где x_i – i- ая компонента (координата) вектора Х.

Понятие n-мерного вектора широко используется в экономике, например, некоторый набор товаров можно охарактеризовать вектором Х = (x₁, x₂,... x_n), где x_i – количество i- го товара, а соответствующие цены можно записать в виде Р = (р₁, р₂,... р_n).

Два n-мерных вектора равны тогда и только тогда, когда равны их соответствующие компоненты: X = Y Û x_i = y_i, i = 1, 2,... n.

Суммой двух векторов одинаковой размерности n называется вектор Z = X + Y, компоненты которого равны сумме соответствующих компонент слагаемых векторов: z_i = x_i + y_i, i = 1, 2,... n.

Произведением вектора Х на действительное число l называется вектор U = l X, компоненты u_i которого равны произведению l на соответствующие компоненты вектора Х: u_i = lx_i, i = 1, 2,... n.

Пусть X, Y, Z – любые векторы одинаковой размерности, a,b - любые числа. Линейные операции над векторами (сумма векторов и умножение вектора на число) удовлетворяют следующим свойствам (аксиомам):

1. X + Y = Y + X;

2. (X + Y) + Z = X + (Y + Z);

3. a(b X) = ( ab )X;

4. a (X + Y) = a X + a Y;

5. (a + b) X = a X + b X;

6. Существует нулевой вектор 0 = (0, 0,..., 0) такой, что X + 0 = X для любого вектора X (особая роль нулевого вектора);

7. Для любого вектора Х существует противоположный вектор (-Х) такой, что Х + (-Х) = 0;

8. 1× Х = Х для любого вектора Х (особая роль числового множителя 1).

Заметим, что под X, Y, Z можно рассматривать не только векторы, но и элементы (объекты) любой природы. В этом случае соответствующее множество элементов называется линейным пространством L.

Определение. Вектор В называется линейной комбинацией векторов А_1, А₂,..., А_n векторного пространства Rⁿ, если он равен сумме произведений этих векторов на произвольные действительные числа: В = a₁ А₁ + a₂ А₂ +...+ a_n А_n, где a_1, a₂,... a_n – любые действительные числа.

Определение. Векторы А_1, А₂,..., А_n называются линейно зависимыми, если существует такая линейная комбинация a₁ А₁ + a₂ А₂ +...+ a_n А_n = 0, при не равных нулю одновременно a_i (i = 1, 2,... n), т.е. .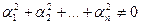

Если же a₁ А₁ + a₂ А₂ +...+ a_n А_n = 0 выполняется только при всех a_i = 0(i = 1, 2,... n), то векторы называются линейно независимыми.

Свойства линейно зависимой системы векторов.

Свойство 1. Если среди векторов А_i ( i = 1, 2,... n) есть нулевой вектор, то эти векторы линейно зависимы.

Свойство 2. Если к системе линейно зависимых векторов добавить один или несколько векторов, то полученная система тоже будет линейно зависима.

Свойство 3. Система векторов линейно зависима тогда и только тогда, когда один из векторов раскладывается в линейную комбинацию остальных векторов.

Геометрический смысл линейной зависимости векторов очевиден для случаев двумерных векторов на плоскости и трехмерных векторов в пространстве:

В случае двух векторов, когда один вектор выражается через другой: 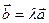, т.е. эти векторы коллинеарны или, что то же самое, они находятся на параллельных прямых.

Свойство 4. Любые 2 коллинеарных вектора линейно зависимы и, наоборот, любые 2 линейно зависимые векторы коллинеарны: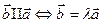

В пространственном случае линейной зависимости трех векторов они параллельны одной плоскости, т.е. компланарны.

Свойство 5. Любые 3 компланарных вектора линейно зависимы и, наоборот, любые 3 линейно зависимые векторы компланарны.

Т.е., достаточно «подправить» соответствующими сомножителями длины этих векторов, чтобы один из них стал суммой двух других (выражался через них).

Утверждение. В пространстве Rⁿ любая система, содержащая m векторов, линейно зависима при m > n.

Дата добавления: 2014-10-31