Вектор. Основные понятия

ЛИНЕЙНАЯ АЛГЕБРА С ЭЛЕМЕНТАМИ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ

I СЕМЕСТР

ГЛАВА 1. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ.

Очень часто для построения экономических моделей требуется простая и i = 1, 2,... n. компактная форма записи сложных экономических процессов. С этой целью будущим экономистам необходимо знать основные понятия и положения такого раздела математики как матричная алгебра. При изложении материала мы будем опираться на понятия и теоремы школьного курса элементарной математики. Например, определения вещественных (действительных) чисел, декартовой системы координат, отображения, точки, прямой, длины отрезка.

Понятие вектора известно из школьного курса математики, но вспомним основные факты, связанные с ним.

Если про две точки известно, какая из них первая, а какая – вторая, то эту пару точек назовем упорядоченной.

Определение. Отрезок, концы которого упорядочены, называется направленным отрезком или вектором. Первый из его концов называется началом, а второй – концом вектора.

В

А

Нулевым вектором называется вектор, начало и конец которого совпадают. Нулевой вектор обозначается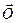. Длина его равна нулю, а направление – любое.

Определение. Длиной (модулем) вектора называется расстояние между началом и концом вектора.

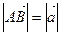
Определение. Векторы называются коллинеарными, если они расположены на одной или параллельных прямых.

Нулевой вектор коллинеарен любому вектору, так как он не имеет определенного направления.

Определение. Для каждого ненулевого вектора вводится понятие противоположного вектора -, который коллинеарен данному, имеет такую же длину, но направлен в противоположную сторону.

Определение. Векторы называются компланарными, если существует плоскость, которой они параллельны.

Коллинеарные векторы всегда компланарны, но не все компланарные векторы коллинеарны.

Определение. Векторы называются равными, если они коллинеарны, одинаково направлены и имеют одинаковые модули.

Всякие векторы можно привести к общему началу, т.е. построить векторы, соответственно равные данным и имеющие общее начало. Из определения равенства векторов следует, что любой вектор имеет бесконечно много векторов, равных ему.

Если компланарные векторы привести к одному началу, то они будут лежать в одной плоскости.

В любой системе координат вектор полностью определяется своими координатами: 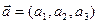. Например, пусть в прямоугольной декартовой системе координат OXYZ координаты начала и конца вектора соответственно A(x₁, y₁, z₁) и B(x_2, y₂, z₂). Тогда координатами этого вектора будут являться его проекции на соответствующие координатные оси и определяются они формулами: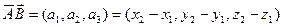

Очевидно, что длина вектора определяется по формуле: .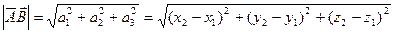

Дата добавления: 2014-10-31