Дифференциальные уравнения движения баллистической ракеты

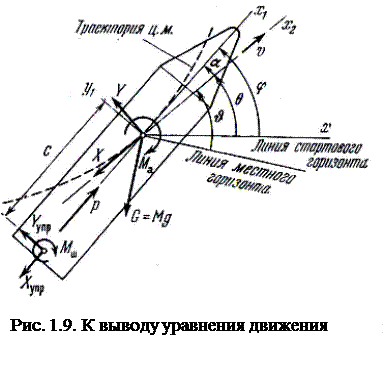Рассмотрим движение ракеты в одной плоскости. Для уча­стка выведения баллистической ракеты такой упрощенный под­ход не ведет к сколь-либо заметным погрешностям.

На рис. 1.9 показана система сил, действующих на ракету при плоском движении. При этом плоскости x₁y₁ и х ₂ у ₂пред­полагаются совпадающи­ми с вертикальной пло­скостью ху.

Согласно закону Нью­тона произведение массы ракеты М на тангенци­альное ускорение dv/dt= и равно сумме проек­ции сил на касательную к траектории. В итоге по­лучаем:

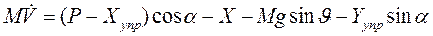(1.2)

Специфические особенности движения ракеты как тела переменной массы здесь уже учтены в выражении тяги Р.

Нормальное ускорение, обусловленное искривлением траек­тории, равно, как известно, , где — радиус кривизны траектории. (На рис. 1.9 траектория показана с положительной кривизной; в действительности ее кривизна отрицательна.)

Выражение кривизны может быть написано в виде

где θ —угол наклона касательной к траектории, отсчитываемый от неподвижного стартового горизонта (рис. 1.9), a ds — эле­мент дуги траектории.

Таким образом, нормальное ускорение, направленное к цент­ру кривизны, оказывается равным .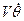

Спроектировав все силы на нормаль к траектории полета, получим:

. (1.3)

Остается составить еще одно уравнение, связанное с враще­нием ракеты как жесткого целого в плоскости тангажа.

Угловое ускорение ракеты определяется второй производной от угла φ по времени. Если бы масса ракеты оставалась неиз­менной, то искомое уравнение мы получили бы, приравняв произведе­ние I 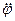сумме моментов, показанных на рис. 1.9. Но дело в том, что I - момент инерции ракеты относительно поперечной оси зависит от времени. Поэтому, для того чтобы со­ставить уравнение вращательного движения в этом простейшем слу­чае, необходимо предварительно проделать операции, подобные тем, которые производились нами ранее при выводе уравнения поступательного движения тела перемен­ной массы.

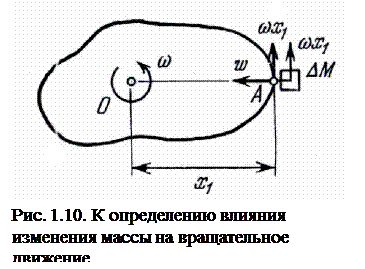
Представим себе некоторое тело (рис. 1.10), которое вращает­ся относительно оси 0 с угловой скоростью ω. Пусть за время Δt к этому телу в радиальном направлении в точке А на расстоя­нии x₁от оси с нулевой относительной круговой скоростью при­соединяется масса ΔM. Момент количества движения тела после присоединения массы ΔM мы формально записываем в виде:

Приравняв изменение момента количества движения им­пульсу моментов M_i внешних сил, получим:

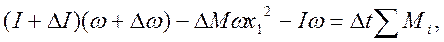
где ωx ₁— поперечная составляющая скорости присоединяемой массы, а — ее момент количества движения до присое­динения.

Затем перейдем к пределу. Тогда

где 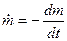— радиальный секундный массовый расход.

В нашем случае 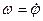. Поэтому . Слагаемое 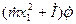, имеющее размерность момента, как раз и отражает специфику переменной массы в условиях вра­щательного движения. Эту величину можно одновременно трак­товать и как некоторый демпфирующий момент кориолисовых сил, возникающих в результате поворота потока частиц, дви­жущихся в баках, трубопроводах и камере двигателя. Подроб­нее мы поговорим об этом при рассмотрении демпфирующих моментов, действующих на ракету.

Теперь можно написать уравнение вращательного движения в плоскости полета в следующем виде:

(1.4)

где момент кориолисовых сил

(1.5)

Система дифференциальных уравнений (1.2) —(1.4) еще не является полной, и не только потому, что описывает движение ракеты в одной плоскости. Как раз для целей баллистических расчетов модель плоской траектории позволяет в достаточной мере точно определить все интересующие нас траекторные па­раметры. Дело совсем в другом.

Уравнения следует дополнить условиями выведения ракеты на активном участке траектории. А это, как мы знаем, обеспечивается, прежде всего, програм­мой изменения угла тангажа.

Таким образом, на три полученных уравнения накладывается условие:

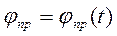(1.6)

Но коль скоро угол 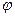заранее известным образом зависит от времени, уравнение (1.4) теряет свою дифференциальную форму и превращается в некоторую функциональную зависи­мость входящих в него величин. Так бы оно и было, если бы ракета в своем движении точно следовала нашим предписа­ниям. Но фактический угол тангажа 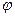в уравнении (1.4) и но­минальный программный угол в выражении (1.6) — не одно и то же. В реальных условиях полета ракета совершает некото­рые угловые колебания относительно поперечных и продольной осей. Частота и амплитуда этих колебаний зависят, конечно, от моментов инерции ракеты, но главное, — от изменения управ­ляющих усилий во времени, в данном случае — от Y _упр. А уп­равляющие усилия, в свою очередь, зависят от принципиальной схемы и параметров настройки автомата стабилизации. Значит, система уравнений (1.2) — (1.4) должна быть дополнена еще уравнениями управления, которые указывают нам, каким обра­зом Y _упр зависит от фактического угла тангажа. Но об этом речь еще впереди.

Сейчас же следует отметить, что уравнения движения (1.2) — (1.4) могут быть положены в основу решения двоякого рода задач: с одной стороны, — баллистических, а с другой, — задач устойчивости, управления и стабилизации. Баллистика как раз­дел механики дает нам закон движения центра масс: координа­ты, скорость, ускорение номинального движения в зависимости от времени. Теория устойчивости движения, со своей стороны, отвечает на вопрос о том, в какой мере в реальных условиях выдерживается угловая ориентация ракеты на траектории. Пер­вый класс задач для участка выведения баллистических ракет, как мы уже сказали, в проектной постановке относительно без­болезненно вписывается в схему плоского движения. Для пол­ного решения задач второго типа необходимо рассматривать угловые перемещения по всем трем осям.

Возвращаясь к структуре уравнений (1.2) — (1.4),.мы видим, что входящие в них величины остаются пока нераскрытыми. Чтобы произвести интегрирование, необходимо знать, что от чего и как зависит.

Совершенно ясно, что аэродинамические силы зависят от скорости, высоты полета и угловой ориентации ракеты относи­тельно потока. Сила тяги не остается постоянной; она меняется хотя бы уже потому, что с высотой меняется атмосферное дав­ление, а, кроме того, может меняться и расход компонентов. Масса ракеты во времени уменьшается в соответствии с расхо­дом топлива. Наконец, даже ускорение силы тяжести g, если речь идет о больших высотах, должно рассматриваться как ве­личина переменная.

Все эти вопросы мы сейчас и рассмотрим. Начнем со свойств атмосферы и аэродинамических сил.

Дата добавления: 2014-10-31