Различные виды уравнений прямой на плоскости

ПРЯМАЯ НА ПЛОСКОСТИ

Задачи для самостоятельного решения

а) Даны векторы 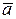= (1, 1, -3), 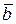= (-2, 2, 1) и 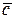= (3, -2, 5). Вычислить .

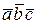б) В треугольной пирамиде с вершинами в точках А (1, 1, 1), В (2, 0, 2), С (2, 2, 2) и D (3, 4, -3) вычислить высоту h = ||.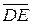

в) Доказать, что четыре точки А (1, 2, 1), В (0, 1, 5), С (-1, 2, 1) и

D (2, 1, 5) лежат в одной плоскости.

Общее уравнение прямой имеет вид

Ах + Ву + С = 0, (8.1)

причем вектор 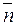= (А, В) ¹ 0. Вектор 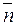является ортогональным к прямой (8.1) и его называют вектором нормали. Если С = 0, то прямая (8.1) проходит через начало координат. Если же С ¹ 0, то после деления уравнения (8.1) на (- С) получаем уравнение прямой в отрезках

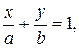(8.2)

где ; , причем (а, 0) и (0, b) - координаты точек пересечения прямой (8.2) с осями координат.

Пример. Составим уравнение прямой, отсекающей на осях координат отрезки а = 0,2, -0,1.

Воспользовавшись уравнением (8.2), имеем

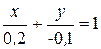или 5 х - 10 у - 1 = 0.

Если в уравнении (8.1) В = 0, то прямая параллельна оси Оy. Если же

В ¹ 0, то уравнение (8.1) можно преобразовать к уравнению прямой с угловым коэффициентом

у = kх + b, (8.3)

где , причем k = tga, а a - угол, образованный прямой с положительным направлением оси Ох. Свободный член b в (8.3) - ордината точки пересечения прямой с осью Оу.

Примеры.

а) Составим уравнение прямой, отсекающей от оси Оу отрезок b = -3 и образующей с этой осью угол b = p/6.

Заметив, что , из уравнения (8.3) выводим у = х· tg a - 3 = х· tg(p/2 -p/6) - 3 = .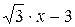

б) Представим общее уравнение прямой 12 х - 5 у - 65 = 0 в виде уравнения в отрезках и уравнения с угловым коэффициентом.

Разрешив общее уравнение прямой относительно у, получим уравнение с угловым коэффициентом: у = 2,4 х - 13 (k = -12/-5=2,4, b = -(-65/-5)= -13).

Разделив общее уравнение прямой на 65 и перенеся 1 направо, получим уравнение в отрезках: (а = 65/12, = - 13).

Если заданы две прямые:

А ₁ х + В ₁ у + С ₁ = 0 или у = k ₁ х + b ₁,

А ₂ х + В ₂ у + С ₂ = 0 или у = k ₂ х + b ₂,

то для острого угла j между ними справедливы формулы:

(8.4)

(8.5)

Отсюда легко получаем условия параллельности прямых:

А ₁/ А ₂ = В ₁/ В ₂ или k ₁ = k ₂ (8.6)

и ортогональности прямых:

А ₁ А ₂ + В ₁ В ₂ = 0, или k ₁ = - 1/ k ₂. (8.7)

Примеры.

а) Определим острый угол между прямыми у = -3х + 7 и у = 2х + 1.

Из формулы (8.5) имеем

tg j = |(2 - (-3))/(1 + (-3)2)| = 5/5 = 1, j = p/4.

б) Покажем, что прямые 4 х - 6 у + 7 = 0 и 20 х - 30 у - 11 = 0 параллельны.

Из условий (8.6) имеем 4/20 = (-6)/(-30) = 1/5, т.е. прямые параллельны.

в) Покажем, что прямые 3 х - 5 у + 7 = 0 и 10 х + 6 у - 3 = 0 ортогональны.

Применяя условие ортогональности (8.7), имеем 3∙10 - 5∙6 = 0 и делаем заключение об ортогональности прямых.

Уравнение прямой, проходящей через точку (х ₀, у ₀) записывается в виде

А(х - х ₀ ) + В(у - у ₀ ) = 0 (8.8)

Дата добавления: 2014-10-31