Построение наклонного сечения

В машиностроительных чертежах встречаются детали, для выявления внутренней конструкции которых следует выполнить наклонное сечение или разрез (рис. 14). Построение изображений должно быть максимально упрощено, поэтому в качестве секущих плоскостей всегда используют плоскости частного положения.

В задании на выполнение расчетно-графической работы «Проекционное чер­чение» предусмотрено построение наклонного сечения. Положение секущей фронтально-проецирующей плоскости задано на виде спереди, с помощью засечек.

Для построения натурального вида наклонного сечения используют способ за­ме­ны плоскостей проекций. Тогда фигура сечения проецируется на дополни­тель­ную плоскость, параллельную секущей плоскости, без искажения.

Любую деталь можно разбить на составляющие её простейшие геометрические фигуры, поэтому рассмотрим сначала построение натурального вида вынесенных наклонных сечений таких фигур.

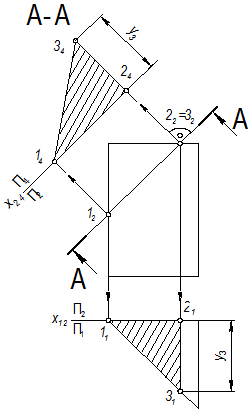
На рис. 28 изображено построение натурального вида сечения призмы фронтально-проецирующей плоскостью А-А, которая пересекает призму по тре­уголь­нику 1-2-3. Фронтальная проекция треугольника совпадает с плоскостью А-А, горизонтальная — проецируется с искажением. Сначала отмечают фронтальные проекции этих точек, а затем по линиям связи находят их горизонтальные проекции.

При построениях нет необходимости фиксировать оси и плоскости проекций — достаточно просто провести в качестве ориентира в произвольном месте чертежа прямую, параллельную секущей плоскости А-А (рис. 29), и отложить на перпен­ди­ку­ля­рах к этой прямой соответствующие расстояния, найденные на горизонтальной проекции.

Рис. 28		Рис. 29

На рис. 29 фронтально-проецирующая плоскость А-А пересекает пирамиду по четырехугольнику 1-2-3-4, который строится по точкам пересечения каждого ребра пирамиды с плоскостью А-А. Сначала отмечают фронтальные проекции этих точек, а затем по линиям связи находят их горизонтальные проекции. Параллельно А-А в произвольном месте проведена прямая-ориентир для построения натуральной величины четырехугольника. На этой прямой находят проекцию 1₄ точки 1, которая расположена на линии связи, перпендикулярной А-А, а остальные точки строят на соответствующих линиях связи относительно прямой-ориентира и 1₄.

За ориентир при построении натуральной величины сечения взята прямая (ось х ₂₄), параллельная плоскости А-А. Расстояния до точек 1, 2, 3 определены по горизонтальной проекции треугольника по правилу: расстояние от новой оси до новой проекции точки равно расстоянию от предыдущей оси до заменяемой проекции точки [3, 4].

Натуральную величину плоского сечения можно определить и способом вращения вокруг фронтально-проецирующей оси i ^ P₂, как это показано на рис. 30. Однако такой способ требует большего места на чертеже, поэтому все последующие примеры выполнены заменой плоскостей проекции, как самым простым способом.

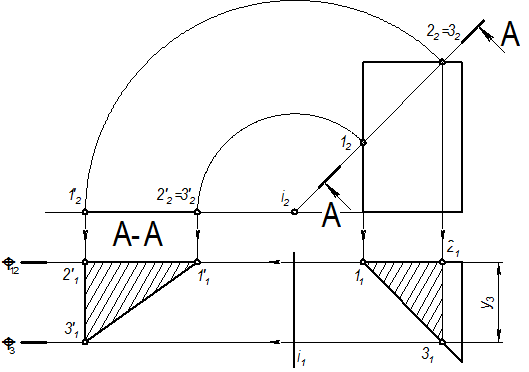
Рис. 30

Фигуру сечения рекомендуется строить в такой же последовательности, в какой секущая плоскость пересекает отдельные элементы детали, например, слева направо, (рис. 29).

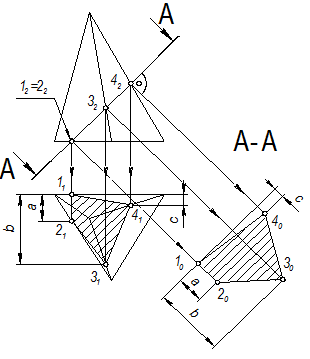
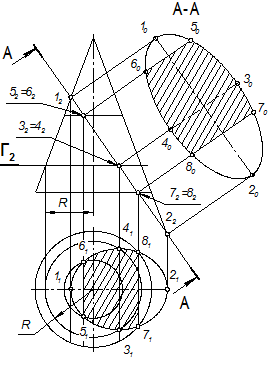
Построение натуральной величины сечения цилиндра и конуса фронтально-проецирующей поверхностью А-А показано на рис. 31 и 32.

Как известно, в рассматриваемых примерах плоскость А-А пересекает цилиндр и конус по эллипсам, а эллипс - фигура симметричная. Если в сечении намечается симметричная фигура, базой для её построения может служить ось симметрии (рис. 31 и рис. 32), которую располагают параллельно заданной секущей плоскости А-А.

Большая ось натуральной величины эллипса равна отрезку 1₂2₂, малая — отрезку 3₁4₁, который проходит через середину большой оси перпендикулярно к ней. Малая ось сечения цилиндра всегда равна его диаметру. Для определения величины малой оси эллиптического сечения конуса проводят вспомогательную горизонтальную плоскость-посредник Г || P₁ через точки 3₂ и 4₂. Эта плоскость пересекает конус по окружности радиуса R, а секущую плоскость А-А по прямой, совпадающей с линией связи. На виде сверху эти линии пересекаются в точках 3₁ и 4₁, которые на горизонтальной плоскости проекций и ограничивают малую ось. На сечении откладывается отрезок, равный найденной величине малой оси эллипса 3₁4₁ = 3₀4₀.

Рис. 31		Рис. 32

Аналогично можно найти любые промежуточные точки натуральной величины сечения. На рис. 31 секущая плоскость пересекает основание цилиндра по хорде 5-6, длину которой определяют по горизонтальной проекции цилиндра (так же, как и расстояния между промежуточными точками 7 и 8). На рис. 32 аналогично построены точки эллипса (5-6 и 7-8), расположенные на основаниях усеченного конуса.

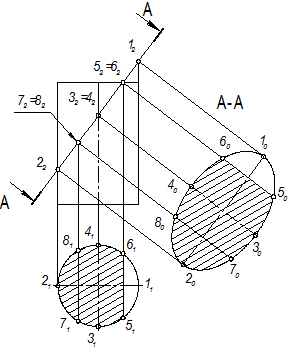
Разберем пример построения вынесенного наклонного сечения А-А, показанного на рис. 33. Разрезы, выполненные на изображениях детали, не отражаются на форме сечения. Прежде чем приступить к выполнению построений, надо тонкими линиями нанести невидимый контур и выявить, какие поверхности пересекаются плоскостью А-А и какие линии требуется построить. После построения наклонного сечения вспо­мо­гательные линии необходимо убрать, чтобы не затемнять чертеж. Для большей ясности на рис. 33 показана горизонтальная проекция сечения (заштрихо­вана), которую обычно не строят. Это вспомогательная проекция, она не дает действитель­ной величины сечения, но помогает при его построении. Фигура сечения симметрич­на, поэтому базой для построения служит ось симметрии. Новую ось проекций — прямую, параллельную секущей плоскости А-А, проводят в произволь­ном свободном месте чертежа. При выполнении РГР рекомендуется эту прямую располагать над основной надписью.

Затем вдоль базовой прямой откладывают отрезки, перенесенные с фронтальной проекции, а по перпендикулярному направлению линии связи в обе стороны от оси сим­метрии откладывают величины, взятые с горизонтальной проекции фигуры сечения.

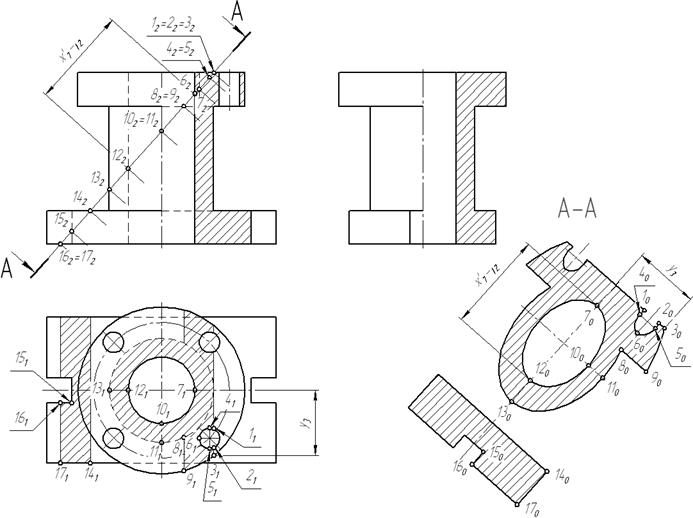
Рис. 33

В качестве примера на рис. 33 показано построение точки 1. Остальные точки строятся аналогично. Секущая плоскость пересекает все образующие внутреннего цилиндра, поэтому в сечении получается эллипс, у которого большая ось определяется по фронтальной проекции как расстояние между точками пересечения крайних образующих 11₂13₂, а малая ось равна диаметру цилиндра.

Четыре других цилиндра пересекаются плоскостью частично, поэтому в сечении получаются только дуги эллипсов. Остальные пересекаемые поверхности — плоскости, которые в сечении дают отрезки прямых.

Для построения контура сечения необходимо соединить проекции найденных то­чек в логической последовательности. Затем выполняют штриховку сечения.

Располагать сечение допускается на любом свободном месте чертежа и вне проекционной связи, то есть со смещением вдоль оси симметрии (рис. 33) или с поворотом. В последнем случае надпись сечения сопровождают знаком «повернуто», который выполняют согласно рис. 10, а.

Итак, любая точка контура сечения может быть построена или проведена по двум координатам, одна из которых измеряется вдоль базовой прямой (размер определяется на виде спереди), а другая — по перпендикулярному направлению (размер определяется на виде сверху).

Дата добавления: 2014-11-06