
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Векторы в декартовой системе координат
|
|
|
|
Выражение физических законов в векторной форме отличается изяществом и лаконичностью. Однако бывает полезно перейти от векторов к определенным системам координат, из которых наиболее удобной является прямоугольная декартовая система координат.
Декартова система координат определяется заданием любой правой тройки взаимно перпендикулярных единичных векторов 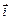 ,
, 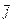 ,
,  . Направление вектора
. Направление вектора  определяется правилом правого винта, т. е.
определяется правилом правого винта, т. е.  .
.
Любой вектор 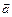 можно выразить так:
можно выразить так:

Здесь 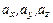 – проекции вектора
– проекции вектора 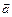 на соответствующие координатные оси:
на соответствующие координатные оси:
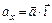 ,
,  ,
,  .
.
Любой вектор считается заданным тройкой чисел (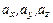 ) в данной системе координат.
) в данной системе координат.
Найдем скалярное произведение двух векторов в декартовой системе координат, воспользовавшись естественными равенствами:
 ,
,  ,
,  ,
,  ,
, 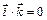 ,
, 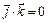 .
.

Для квадрата вектора 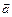 имеем
имеем
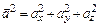 .
.
Векторное произведение единичных векторов равно:
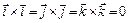 ,
, 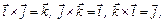
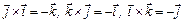 ,
,
поэтому векторное произведение двух векторов равно:

Эквивалентная запись векторного произведения через определитель:
 .
.
1.1
 |
Определите проекции на оси ОX и OY векторов представленных на рисунке 1.
Пример:  ;
; 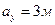
1.2 Запишите векторы представленные на рисунке 1 в декартовой системе координат (через единичные орты осей ОX и OY  и
и 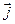 ).
).
Пример: 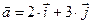
1.3 Найдите сумму векторов с рисунка 1 графически и аналитически:
а) 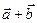 ; б)
; б) 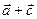 ;в)
;в)  ; г)
; г)  ; д)
; д)  ; е)
; е) 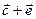 ; ж)
; ж) 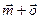 ; з)
; з)  ; и)
; и)  ; к)
; к) 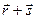 ; л)
; л) 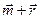 ; м)
; м)  ; н)
; н) 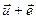 ; о)
; о)  .
.
Пример: 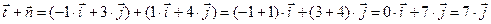
1.4 Найдите разность векторов с рисунка 1 графически и аналитически:
а) 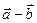 ; б)
; б)  ;в)
;в) 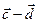 ; г)
; г)  ; д)
; д) 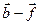 ; е)
; е)  ; ж)
; ж)  ; з)
; з) 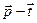 ; и)
; и) 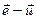 ; к)
; к)  ; л)
; л) 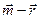 ; м)
; м) 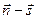 ; н)
; н) 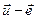 ; о)
; о) 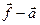 .
.
Пример: 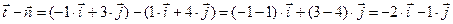
1.5 Определите скалярное произведение двух векторов с рисунка 1
а)  ; б)
; б)  ;в)
;в)  ; г)
; г)  ; д)
; д)  ; е)
; е) 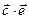 ; ж)
; ж)  ;
;
з)  ; и)
; и)  ; к)
; к)  ; л)
; л)  ; м)
; м)  ; н)
; н) 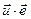 ; о)
; о)  .
.
Пример: 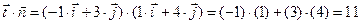
1.6 Определите векторное произведение двух векторов с рисунка 1
а)  ; б)
; б)  ;в)
;в)  ; г)
; г)  ; д)
; д) 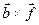 ; е)
; е) 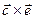 ; ж)
; ж)  ;
;
з) 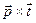 ; и)
; и)  ; к)
; к) 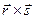 ; л)
; л)  ; м)
; м)  ; н)
; н) 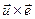 ; о)
; о) 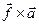 .
.
Пример: 
Приложение 2
Основы математического анализа
Если функция f имеет в точке x производную, то существует предел:
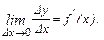 где
где  .
.
Отсюда следует, что
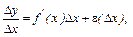 где
где 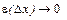 при
при 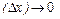
Таким образом,  (1)
(1)
Если ввести обозначение  , то равенство (1) можно записать следующим образом:
, то равенство (1) можно записать следующим образом:
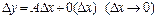 (2)
(2)
говорят, что функция f дифференцируема в точке если ее приращение Dy в этой точке можно записать в виде (2), где А – некоторая константа, не зависящая от Dx, но вообще говоря зависящая от x. Если функция 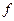 имеет в точке x производную, то она дифференцируема в этой точке (
имеет в точке x производную, то она дифференцируема в этой точке ( ). Верно и обратное утверждение: если функция дифференцируема в точке x, т. е. ее приращение в точке x представимо в виде (2), то она имеет производную в точке x равную А.
). Верно и обратное утверждение: если функция дифференцируема в точке x, т. е. ее приращение в точке x представимо в виде (2), то она имеет производную в точке x равную А.
Если 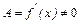 , то приращение функции эквивалентно при
, то приращение функции эквивалентно при  первому слагаемому правой части (2)
первому слагаемому правой части (2)  (
( ). В этом случае, когда
). В этом случае, когда  , член
, член 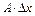 называют главным линейным членом приращения. Приближенно, пренебрегая бесконечно малой
называют главным линейным членом приращения. Приближенно, пренебрегая бесконечно малой 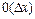 высшего порядка, при малых
высшего порядка, при малых 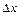 можно считать
можно считать 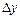 равным главному члену.
равным главному члену.
Главный линейный член приращения называют дифференциалом функции 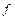 в точке
в точке 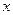 (соответствующим приращению
(соответствующим приращению 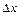 независимой переменной
независимой переменной 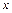 ) и обозначают так:
) и обозначают так:
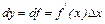 .
.
Приращение 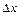 независимой переменной обозначают
независимой переменной обозначают  (
( для дифференциала функции
для дифференциала функции 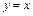 от
от 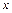 ), таким образом дифференциал функции
), таким образом дифференциал функции 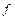 в точке
в точке 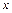 записывается так
записывается так
 .
.
Отметим очевидные формулы:

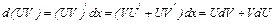
 .
.
Производная функции от функции
Пусть задана функция от функции  , где
, где  ,
, 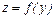 . При этом функция
. При этом функция 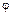 имеет производную в точке
имеет производную в точке 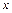 , а функция
, а функция 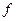 имеет производную в точке
имеет производную в точке 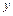 . Тогда существует производная от
. Тогда существует производная от 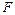 в точке
в точке 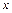 , равная:
, равная:
 .
.
Таблица производных простейших элементарных функций.
1. 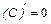

2. 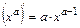 , а – любое число
, а – любое число
3. 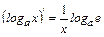 , в частности
, в частности 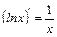
4. 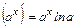 , в частности, при
, в частности, при  :
: 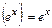
5. 
6. 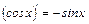
7. 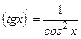
8. 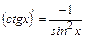
9. 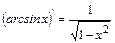
10. 
11. 
12. 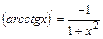
|
|
|
|
|
Дата добавления: 2014-11-06; Просмотров: 934; Нарушение авторских прав?; Мы поможем в написании вашей работы!