Характеристика электромагнитных колебаний

ИЗУЧЕНИЕ ЗАТУХАЮЩИХ КОЛЕБАНИЙ

Лабораторная работа № 44

Цель работы – экспериментально и теоретически установить зависимости периода колебаний Т, логарифмического декремента Θ, добротности Q от параметров контура (R, L, C).

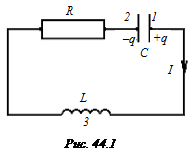Идеальный колебательный контур состоит из конденсатора ёмкостью С и катушки индуктивностью L. После сообщения конденсатору заряда q₀, в контуре появилась разность потенциалов (напряжение U между обкладками конденсатора), следовательно система (колебательный контур) выведена из равновесного состояния. Заряд конденсатора начнёт убывать (конденсатор разряжается) и в цепи появится нарастающий электрический ток. Протекая через катушку, переменный ток породит в ней ЭДС самоиндукции, которая препятствует нарастанию тока, то есть появилась «возвращающая сила». Когда заряд и напряжение на конденсаторе станут равными нулю, а ток в цепи достигнет максимального значения, процесс «повернёт обратно», то есть ток через катушку начнёт убывать, а заряд на конденсаторе возрастать. Убывающий ток в катушке породит ЭДС самоиндукции, препятствующую убыванию тока. На обкладках конденсатора будет накапливаться заряд противоположный по знаку начальным. Когда ток через катушку станет равным нулю, завершился один цикл, то есть прошёл по времени один период. За период конденсатор заряжается и разряжается по 2 раза.

В реальном колебательном контуре (рис. 44.1) существует активное сопротивление R и при протекании электрического тока (по закону Джоуля-Ленца), проводники нагреваются. Вследствие этого энергия электромагнитного поля, первоначально запасенная в контуре, непрерывно расходуется на выделение тепла в сопротивлении R, что приведёт к постепенному затуханию колебаний. Таким образом, в реальном контуре свободные электромагнитные колебания являются затухающими.

Чтобы найти уравнение колебаний в контуре, воспользуемся правилом Кирхгофа:

, (44.1)

где U_R – напряжение на сопротивлении, U_C- напряжение на конденсаторе, e - ЭДС самоиндукции.

Выражая в (44.1) напряжения , и ЭДС самоиндукции e через заряд конденсатора q и параметры контура, получим дифференциальное уравнение затухающих колебаний в контуре

. (44.2)

Введём постоянные коэффициенты

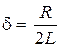-коэффициент затухания (44.3)

и

-собственная частота контура, то есть частота свободных незатухающих колебаний без потерь энергии (при R=0). (44.4)

Тогда уравнение (44.2) можно преобразовать к виду:

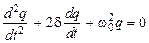. (44.5)

Если затухание мало, т. е. < 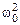, решение уравнения (44.5) имеет вид

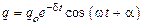, (44.6)

где

- циклическая частота затухающих колебаний в контуре. (44.7)

Таким образом, при замыкании заряженного конденсатора на цепь из последовательно соединенных катушки индуктивностью L и резистора сопротивлением R, заряд на обкладках конденсатора изменяется с течением времени согласно выражению (44.6). Частота затухающих колебаний w определяется параметрами контура R, L, С, причем w < w₀. Если же активное сопротивление контура R =0, то w = w₀.

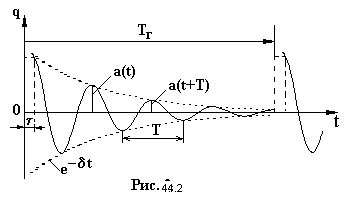
Затухающие колебания не являются, строго говоря, периодическим процессом, так как изменяющаяся со временем величина, например, заряд, не принимает одинакового значения через промежуток времени, равный периоду колебаний Т. Тем не менее, в рассматриваемом случае, когда затухание мало, можно говорить о затухающих колебаниях, как о периодических (рис. 44.2).

Дата добавления: 2014-11-06