
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Матричные игры
|
|
|
|
Транспортная задача
Задача линейного программирования
Сетевое планирование.
Матричные игры.
Рассмотрим пример задачи линейного программирования:


В этой задаче требуется найти наибольшее значение функции  на множестве решений данной системы.
на множестве решений данной системы.
Так как задача содержит две переменные, то её можно решить графически.
Множество решений системы представляет собой многоугольник. Для того, чтобы его построить сначала проведём прямые:
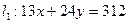 ,
,
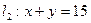 ,
,
 ,
,
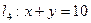 .
.
Каждая прямая разбивает плоскость на две полуплоскости. Одна из полуплоскостей определяет множество решений соответствующего неравенства системы. Полуплоскость определяется с помощью контрольной точки, например (0;0).
Пересечением построенных полуплоскостей является шестиугольник  :
:
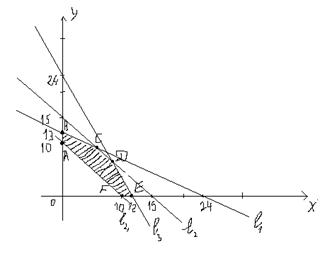
Для нахождения наибольшего значения функции  построим из начала координат градиент функции
построим из начала координат градиент функции 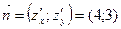 и перпендикулярную ему линию уровня
и перпендикулярную ему линию уровня  , то есть прямую
, то есть прямую 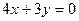 .
.

Далее проводим прямую через многоугольник  , параллельную линии уровня
, параллельную линии уровня  . Затем эту прямую передвигаем параллельно самой себе в направлении вектора
. Затем эту прямую передвигаем параллельно самой себе в направлении вектора  . В последней пересекаемой вершине
. В последней пересекаемой вершине 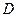 получаем наибольшее значение функции
получаем наибольшее значение функции  . Вершина
. Вершина 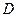 это точка пересечения прямых
это точка пересечения прямых  и
и 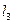 .
.
Координаты точки 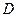 находят из системы уравнений:
находят из системы уравнений:
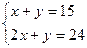
Система имеет решение 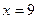 ,
,  .
.
Следовательно,  - наибольшее значение.
- наибольшее значение.
Для того, чтобы найти наименьшее значение функции надо прямую, параллельную линии уровня  , передвигать в противоположном направлении.
, передвигать в противоположном направлении.
Транспортная задача - задача о наиболее экономном плане перевозок однородного груза из пунктов отправления в пункты назначения.
Предположим, что в пунктах отправления  находится однородный груз в количестве 200, 205, 225 единиц. Груз требуется перевезти в пункты потребления
находится однородный груз в количестве 200, 205, 225 единиц. Груз требуется перевезти в пункты потребления  , потребности которых составляют 190, 130, 80, 100, 130 единиц. Стоимости
, потребности которых составляют 190, 130, 80, 100, 130 единиц. Стоимости 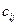 перевозки единицы груза из каждого пункта отправления
перевозки единицы груза из каждого пункта отправления 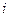 в каждый пункт назначения
в каждый пункт назначения 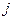 известны и записаны в транспортной таблице:
известны и записаны в транспортной таблице:
| B A | 
| 
| 
| 
| 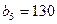
|

| 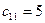
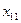
| 
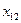
| 
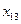
| 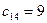

| 

|

| 
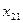
| 
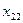
| 
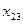
| 

| 

|

| 
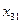
| 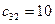
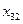
| 

| 

| 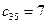

|
В транспортной таблице  - количество груза, перевозимое из пункта
- количество груза, перевозимое из пункта 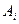 в пункт
в пункт  .
.
Требуется найти такие  , чтобы суммарная стоимость перевозок была бы минимальная.
, чтобы суммарная стоимость перевозок была бы минимальная.
Транспортная задача называется закрытой, если  . В противном случае открытой. От открытой задачи всегда можно перейти к закрытой.
. В противном случае открытой. От открытой задачи всегда можно перейти к закрытой.
Если  , то вводят фиктивный пункт потребления с потребностью
, то вводят фиктивный пункт потребления с потребностью  с нулевыми стоимостями перевозок.
с нулевыми стоимостями перевозок.
Если  , то вводят фиктивный пункт отправления с запасами
, то вводят фиктивный пункт отправления с запасами  с нулевыми стоимостями перевозок.
с нулевыми стоимостями перевозок.
Закрытую транспортную задачу решают методом потенциалов.
Первый план перевозок находят методом северо-западного угла. Он заключается в том, что последовательно вывозится груз из каждого пункта отправления в пункты назначения  .
.
Первый план перевозок можно найти методом наименьшей стоимости:
в клетке (2,3) наименьшая стоимость 3 и туда отправляем весь необходимый груз 80. Далее наименьшая стоимость 4 в клетках (2,4) и (2,2). В клетку (2,4) направляем все 100 единиц необходимого груза, а в клетку (2,2) – оставшиеся в пункте 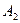 25 единиц груза. Теперь наименьшая стоимость 5 в клетках (1,1) и (1,5). В клетку (1,1) направляем 190 единиц необходимого груза, а в клетку (1,5) – 10 единиц груза оставшегося а пункте
25 единиц груза. Теперь наименьшая стоимость 5 в клетках (1,1) и (1,5). В клетку (1,1) направляем 190 единиц необходимого груза, а в клетку (1,5) – 10 единиц груза оставшегося а пункте 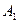 . Затем направляем 120 единиц груза в клетку (3,5) и 105 единиц груза в клетку (3,2). Получим первый план перевозок:
. Затем направляем 120 единиц груза в клетку (3,5) и 105 единиц груза в клетку (3,2). Получим первый план перевозок:
Проверим оптимальность полученного плана перевозок методом потенциалов.
Для того чтобы некоторый план перевозок был оптимальным, необходимо и достаточно, чтобы ему соответствовала система чисел  , удовлетворяющая условиям:
, удовлетворяющая условиям:

для занятых клеток и

для свободных клеток.
Числа  называются потенциалами соответственно поставщиков и потребителей.
называются потенциалами соответственно поставщиков и потребителей.
Найдём потенциалы:
 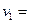 5 5
|
 8 8
|
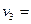 7 7
|
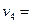 8 8
|
 5 5
| |
 0 0
| |||||
 -4 -4
| |||||
 2 2
|
Так как для клетки (3,3) не выполняется условие оптимальности, то перейдём к следующему плану. В клетку (3,3) направим  единиц груза и перераспределим груз в занятых клетках:
единиц груза и перераспределим груз в занятых клетках:
| 25+t | 80-t | ||||
| 105-t | t |
Перераспределение производим так, чтобы в строке было бы только два  и в столбце – два
и в столбце – два  .
.
Подберём  такое, чтобы одна из занятых клеток стала свободной. Это возможно при
такое, чтобы одна из занятых клеток стала свободной. Это возможно при 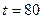 .
.
Новый план имеет вид:
Найдём потенциалы:
 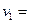 5 5
|
 8 8
|
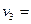 4 4
|
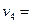 8 8
|
 5 5
| |
 0 0
| |||||
 -4 -4
| |||||
 2 2
|
Для клетки (3,4) условие оптимальности не выполняется. В эту клетку направим  единиц груза и перераспределим груз в занятых клетках.
единиц груза и перераспределим груз в занятых клетках.
| 105+t | 100-t | ||||
| 25-t | t |
Возьмём  . Новый план имеет вид:
. Новый план имеет вид:
Проверим план на оптимальность:
 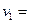 5 5
|
 6 6
|
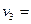 4 4
|
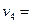 6 6
|
 5 5
| |
 0 0
| |||||
 -2 -2
| |||||
 2 2
|
Полученный план является оптимальным.
Транспортные расходы при этом будут минимальными:
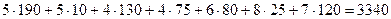 .
.
Рассмотрим следующую игру. Дана матрица, предположим размера 3 4,
4,
 .
.
Два игрока независимо друг от друга выбирают номера строк и столбцов. Если первый игрок выбирает 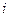 строку, а второй
строку, а второй 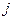 столбец, то элемент
столбец, то элемент 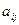 есть выигрыш первого игрока и одновременно проигрыш второго.
есть выигрыш первого игрока и одновременно проигрыш второго.
Стратегией первого игрока называется вектор  , где
, где  - вероятность выбора
- вероятность выбора 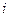 строки.
строки.
Стратегией второго игрока называется вектор  , где
, где  - вероятность выбора
- вероятность выбора 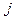 строки.
строки.
Если одна координата стратегии равна 1, а остальные – 0, то она называется чистой, в противном случае – смешанной.
Первый игрок располагает тремя чистыми стратегиями:
 ,
,  ,
,  .
.
Второй – четырьмя:
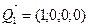 ,
,  ,
,  ,
,  .
.
Средний выигрыш первого игрока равен:
 .
.
Стратегии  и
и  называются оптимальными, если выполняется неравенство:
называются оптимальными, если выполняется неравенство:
 ,
,
где  и
и  произвольные стратегии.
произвольные стратегии.
Средний выигрыш 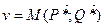 называется ценой игры.
называется ценой игры.
Для оптимальности стратегий  и
и  необходимо и достаточно выполнения условия:
необходимо и достаточно выполнения условия:
 .
.
Отсюда следует, что игра имеет решение в чистых стратегиях тогда и только тогда, когда существует элемент матрицы минимальный в своей строке и в тоже время максимальный в столбце. Номер строки и номер столбца, которые имеет этот элемент, определяют седловую точку. Для существования седловой точки необходимо и достаточно, чтобы  , где
, где  - называется нижним значением игры,
- называется нижним значением игры,  - называется верхним значением игры.
- называется верхним значением игры.
Рассмотрим графическое решение игры  .
.
Для определённости рассмотрим игру  :
:
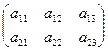 .
.
Найдём оптимальную стратегию первого игрока  . Так как
. Так как  , то
, то
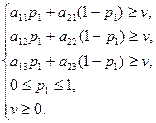
Найдём такое  , при котором
, при котором  принимает максимальное значение. Полученная задача – задача линейного программирования с двумя переменными
принимает максимальное значение. Полученная задача – задача линейного программирования с двумя переменными  и
и  , которую можно решить графическим методом. Задача имеет решение, если элементы матрицы неотрицательны. Пусть в точке
, которую можно решить графическим методом. Задача имеет решение, если элементы матрицы неотрицательны. Пусть в точке 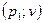 пересечения первой и второй прямой выигрыш первого игрока наибольший, тогда оптимальная стратегия второго игрока имеет вид
пересечения первой и второй прямой выигрыш первого игрока наибольший, тогда оптимальная стратегия второго игрока имеет вид 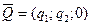 . Координату
. Координату  находят из уравнения
находят из уравнения 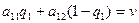 .
.
Рассмотрим графическое решение игры  .
.
Для определённости рассмотрим игру  :
:
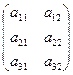 .
.
Найдём оптимальную стратегию второго игрока  . Так как
. Так как 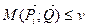 , то
, то

Найдём такое  , при котором
, при котором  принимает минимальное значение. Полученная задача – задача линейного программирования с двумя переменными
принимает минимальное значение. Полученная задача – задача линейного программирования с двумя переменными  и
и  , которую можно решить графическим методом. Задача имеет решение, если элементы матрицы неотрицательны. Пусть в точке
, которую можно решить графическим методом. Задача имеет решение, если элементы матрицы неотрицательны. Пусть в точке  пересечения первой и второй прямой выигрыш второго игрока наименьший, тогда оптимальная стратегия первого игрока имеет вид
пересечения первой и второй прямой выигрыш второго игрока наименьший, тогда оптимальная стратегия первого игрока имеет вид  . Координату
. Координату  находят из уравнения
находят из уравнения  .
.
Задача 12. Найти оптимальные стратегии игроков и цену игры
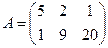 .
.
Решение.
Найдём оптимальную стратегию первого игрока  .
.
Для этого составим задачу линейного программирования:


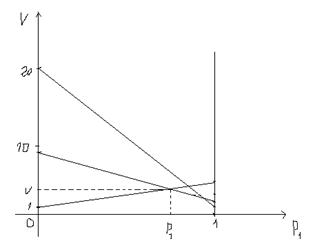
Решением является точка с координатами 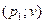 . Эта точка - пересечение прямой
. Эта точка - пересечение прямой  и прямой
и прямой 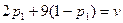 :
:
 ,
,
 ,
,
 ,
, 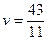 .
.
Оптимальная стратегия первого игрока 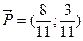 , цена игры
, цена игры 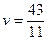 .
.
Оптимальная стратегия второго игрока имеет вид 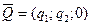 . Координату
. Координату  находят из уравнения
находят из уравнения  . Уравнение имеет решение
. Уравнение имеет решение 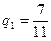 .
.
Следовательно,  .
.
|
|
|
|
|
Дата добавления: 2014-10-15; Просмотров: 425; Нарушение авторских прав?; Мы поможем в написании вашей работы!