Сетевое планирование

Сетевое планирование применяют для организации и выполнения некоторых работ, например, строительство большого объекта. Порядок выполнения работ можно определить с помощью метода критического пути. Для использования этого метода нужно разбить проект на отдельные операции, выяснить очерёдность их выполнения и определить время, необходимое для выполнения каждой операции. Всё это обычно вносится в таблицу:

Операция	Предшествующие операции	Время
	-
	-
	-

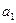
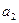
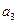
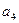
Далее строят ориентированный граф. Дуги графа являются операциями, а вершины – событиями. Операции изображают сплошными линиями. В графе могут быть дуги, которые являются связями. Они изображаются пунктирными линиями. Временем наступления события считают время, когда завершено выполнение всех операций, входящих в соответствующую вершину.

Построенный граф называется сетевым графиком.

После построения сетевого графика нумеруют его вершины. Нумерацию, при которой номер начала любой дуги меньше номера её конца, называют правильной. Пусть вершины сетевого графика. Если продолжительность операции , то её записывают на соответствующей дуге.

Пример правильной нумерации сетевого графика с продолжительностями операций:

Пусть в вершину 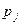входят работы , то ранний срок наступления события равен .

Пусть из вершины выходят работы , то поздний срок наступления события равен .

Ранний срок наступления конечного события называется критическим временем и обозначается .

Всякий путь длины равной из начальной вершины в конечную называется критическим путём.

Поздний срок наступления конечного события, как правило, полагают равным .

Каждой вершине присвоим ранний срок наступления события, номер соответствующей вершины и поздний срок наступления события:

Построение критического пути начинают с конечной вершины. Её вторая координата определяет вершину критического пути. Вторая координата этой вершины определяет ещё одну вершину критического пути и так далее до начальной вершины. На рисунке критический путь выделен волнистой линией:

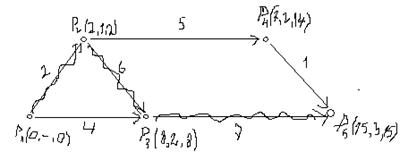
Найдём время, которое можно выделить для выполнения работы без задержки срока окончания всего проекта. Работа не может быть начата раньше срока 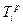и должна быть закончена не позднее времени . Для выполнения этой работы нужно затратить не более единиц времени. По плану работу можно сделать за единиц времени. Максимально допустимое время, на которое можно увеличить продолжительность работы , называется полным резервом времени. Полный резерв времени равен:

.

Очевидно, что полный резерв времени работ, лежащих на критическом пути, равен нулю.

Дата добавления: 2014-10-15