Обнаружение вирусов

Определение 2.3.

Алгоритм A обнаруживает вирус V для любой программы p: A(p) завершает работу и печатает 1 .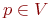

Аналогично, алгоритм A обнаруживает множество вирусов S для любой программы p: A(p) завершает работу и печатает 1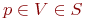

По сути это то же определение обнаружения, что и использованное Ф. Коэном в его дебютной работе.

Полученный Ф. Коэном результат, о том, что не существует алгоритма A, способного обнаруживать множество всех возможных компьютерных вирусов, можно расширить и вывести, что даже имея один из экземпляров вируса V, нельзя создать алгоритм, способный обнаруживать все экземпляры вируса V.

Доказательство этого факта строится по той же схеме, что и доказательство Ф. Коэна. Рассмотрим такой полиморфный вирус, что для любого реализуемого алгоритма X программа p:

• если X(p), то прекратить работу, иначе размножаться
• будет являться экземпляром этого вируса (при условии, конечно, что такая программа вообще способна размножаться)

Очевидно, не существует алгоритма B, который был бы способен обнаруживать все экземпляры такого вируса, поскольку для любого алгоритма B, претендующего на роль детектора, существует программа q:

• если B(q), то прекратить работу, иначе размножаться
• для которой алгоритм B будет возвращать неверный результат. Действительно, если B(q) возвращает 1, значит q никогда не размножается и не является экземпляром описанного или любого другого вируса. Если же B(q) возвращает 0, тогда q в действительности размножается и является экземпляром вируса.

Возникает вопрос о существовании подобного полиморфного вируса и ответ на этот вопрос положительный. Рассмотрим следующий вирус W одним из экземпляров которого является r:

если Sub1(r), то завершить работу, иначе {

заменить текст подпрограммы Sub1 текстом произвольной программы;

размножаться;

завершить работу;

}

Sub1:

Вернуть 0;

Для любого алгоритма C, претендующего на обнаружение всех экземпляров вируса W, найдется программа s:

если Sub1(s), то завершить работу, иначе {

заменить текст подпрограммы Sub1 текстом произвольной программы;

размножаться;

завершить работу;

}

Sub1:

Вернуть С(аргумент);

для которой алгоритм С возвращает ошибочный результат. Если С(s) возвращает 1, значит s всегда просто завершает свою работу и не является экземпляром вируса W или любого другого вируса. Если же C(s) возвращает 0, значит s является экземпляром W. Соответственно, не существует алгоритма C, способного безошибочно определять все экземпляры вируса W и только их.

Дата добавления: 2014-11-20