Машина Тьюринга

Вычислительная машина с хранением программ в памяти с произвольной выборкой

Развитием формализма вычислительной машины с произвольной выборкой является вычислительная машина с хранением программ в памяти с произвольной выборкой (Random Access Stored Program Machine, RASPM), отличие которой состоит только в том, что программа сохраняется в памяти, а значит может изменять сама себя в процессе выполнения.

Набор инструкций для RASPM в общем случае может не отличаться от набора инструкций RAM. Впрочем, некоторые инструкции могут быть упрощены. Так, вместо непрямой адресации можно использовать возможность модификации инструкций программы для получения того же эффекта.

Известно, что имеют место две теоремы:

Теорема 2.1. Если стоимость инструкции является величиной постоянной или находится в логарифмической зависимости от длины операнда, то для любой программы RAM, имеющей сложность T(n), найдется константа k и эквивалентная программа RASPM, сложность которой будет не больше kT(n).

Теорема 2.2. Если стоимость инструкции является величиной постоянной или находится в логарифмической зависимости от длины операнда, то для любой программы RASPM, имеющей сложность T(n), найдется константа k и эквивалентная программа RAM, сложность которой будет не больше kT(n).

Большинство теоретических результатов относительно вычислительной способности различных автоматов (к которым относятся RAM и RASPM) получено для Машины Тьюринга. Следовательно, для применения к RASPM уже известных результатов, необходимо установить отношение между этими формальными системами.

Определение 2.5. Машина Тьюринга с одной лентой может быть определена как совокупность семи элементов:

,

где Q - множество состояний Машины Тьюринга, S - множество символов, которые могут быть записаны на ленте, I - множество символов входящей последовательности, 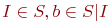- пустой символ, q₀ - начальное состояние Машины Тьюринга, q_f - конечное состояние Машины Тьюринга, d: Q x S -> Q x S x {l, r, s} - множество функций перехода, которые состоянию и символу ленты ставят в соответствие новое состояние, новый символ и перемещение по ленте: на шаг влево, на шаг вправо, остаться на месте

Машина начинает свою работу в состоянии q₀ и в дальнейшем меняет состояния согласно функциям перехода в зависимости от текущего состояния и значения ячейки ленты. Попутно ячейки ленты перезаписываются новыми значениями согласно тем же функциям перехода.

Машина Тьюринга может содержать и большее количество лент, но вычислительная способность такой машины будет находиться в полиномиальной зависимости от вычислительной способности Машины Тьюринга с одной лентой. Помимо этого имеют место следующая теорема:

Теорема 2.3. Вычислительные способности Машины Тьюринга и RASPM эквивалентны, а их затраты на вычисление полиноминально сравнимы, если стоимость выполнения инструкции является величиной постоянной или находится в логарифмической зависимости от длины операнда

Кроме того доказан фундаментальный результат.

Теорема 2.4. Не существует такой Машины Тьюринга, которая сможет определить остановится ли произвольная Машина Тьюринга на произвольном входе (проблема остановки)

Дата добавления: 2014-11-20