Операции над комплексными числами

Суммой комплексных чисел 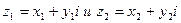называют комплексное число 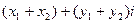Его обозначают 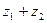. Таким образом,

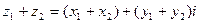(2)

При сложении комплексных чисел складываются их действительные и мнимые части.

Комплексное число 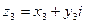называется разностью двух комплексных чисел 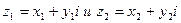, если 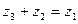. Разность комплексных чисел 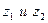обозначается .

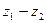Из определения следует, что

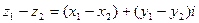. (3)

При вычитании из действительной и мнимой части уменьшаемого соответственно вычитается действительная и мнимая часть вычитаемого.

Умножение двух комплексных чисел 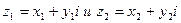вводится равенством

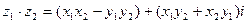. (4)

Равенство (4) следует, из

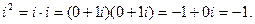(5)

Действительно,

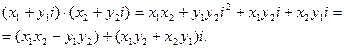
Если при умножении двух комплексных чисел 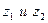получится некоторое число 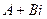, то при умножении сопряженных им чисел 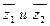получится число сопряженное, т. е. .

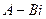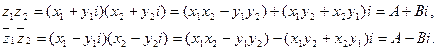
Деление вводится как действие, обратное умножению. Частным от деления числа 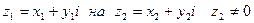называют число 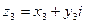, такое, что 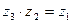, т. е.

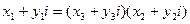. (6)

Отсюда, на основании равенства (4), получаем:

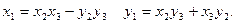(7)

Решая систему (7) относительно 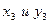находим:

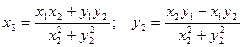(8)

(где 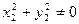, так как по условию ).

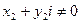Таким образом,

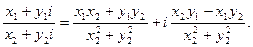(9)

Нетрудно заметить, что равенство (9) может быть получено путем умножения числителя и знаменателя дроби 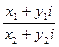на число, комплексно сопряженное знаменателю.

Возведение комплексного числа z в натуральную степень п рассматривается как частный случай умножения комплексных чисел:

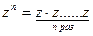
Комплексные числа можно рассматривать как расширение множества действительных чисел. В самом деле, алгебраические операции над комплексными числами введены так, что совокупность всех «действительных» комплексных чисел (т. е. чисел вида 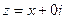или, короче,

z = x с указанными операциями над ними совпадает с совокупностью действительных чисел и известными действиями над этими числами.

Тригонометрическая форма комплексного числа. Выберем на плоскости XOY полярную систему координат (рис. 1) так, чтобы полюс совпал с началом координат, а полярная ось пошла бы по положительному направлению действительной оси. Обозначим полярный радиус точки через ρ, а полярный угол через φ. Полярный радиус ρ называется модулем комплексного числа и обозначается 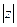. Полярный угол φ называется аргументом комплексного числа и обозначается arg z, если берется главное значение угла 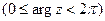, и Argz, если берется общее значение угла. Таким образом,

,

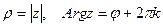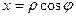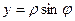где k — произвольное целое число, а φ — любое из значений аргумента z. Так как , а , то

(*)

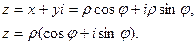Выражение (*) называется тригонометрической формой записи комплексного числа. Очевидно, что

Например,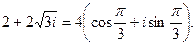

Геометрическая интерпретация сложения комплексных чисел. Пусть плоскости комплексной переменной даются два числа 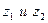(рис. 2).

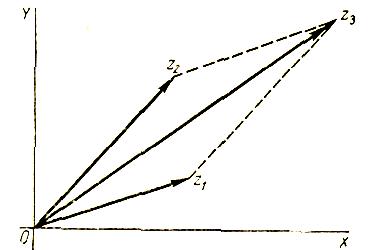
Рис. 2.

Проведя радиусы-векторы точек 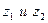получим два вектора 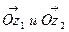, которые соответствуют комплексным числам 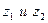. При сложении комплексных чисел складываются их действительные и мнимые части, а при сложении векторов складываются соответствующие координаты. Это позволяет сложение комплексных чисел представлять в виде сложения векторов. Вектор 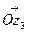, являющийся диагональю параллелограмма, построенного на векторах 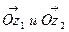и представляет комплексное число: .

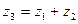Дата добавления: 2014-11-08