КУРС ФИЗИКИ 28 страница

Чувствительность человеческого уха различна для разных частот. Для того чтобы вызвать звуковое ощущение, волна должна обладать некоторой минимальной интенсив­ностью, но если эта интенсивность превышает определенный предел, то звук не слышен и вызывает только болевое ощущение. Таким образом, для каждой частоты колебаний существуют наименьшая (порог слышимости) и наибольшая (порог болевого ощущения) интенсивности звука, которые способны вызвать звуковое восприятие. На рис. 223 представлены зависимости порогов слышимости и болевого ощущения от частоты звука. Область, расположенная между этими двумя кривыми, является областью слышимости.

Если интенсивность звука является величиной, объективно характеризующей вол­новой процесс, то субъективной характеристикой звука, связанной с его интенсив­ностью, является громкость звука, зависящая от частоты. Согласно физиологическому закону Вебера — Фехнера, с ростом интенсивности звука громкость возрастает по логарифмическому закону. На этом основании вводят объективную оценку громкости звука по измеренному значению его интенсивности:

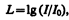
где I ₀ — интенсивность звука на пороге слышимости, принимаемая для всех звуков равной 10^–12 Вт/м². Величина L называется уровнем интенсивности звука и выражается в белах (в честь изобретателя телефона Белла). Обычно пользуются единицами, в 10 раз меньшими, — децибелами (дБ).

Физиологической характеристикой звука является уровень громкости, который вы­ражается в фонах (фон). Громкость для звука в 1000 Гц (частота стандартного чистого тона) равна 1 фон, если его уровень интенсивности равен 1 дБ. Например, шум в вагоне метро при большой скорости соответствует»90 фон, а шепот на расстоянии 1м —»20 фон.

Реальный звук является наложением гармонических колебаний с большим набором частот, т. е. звук обладает акустическим спектром, который может быть сплошным (в некотором интервале присутствуют колебания всех частот) и линейчатым (присутству­ют колебания отделенных друг от друга определенных частот).

Звук характеризуетсяпомимо громкости еще высотой и тембром. Высота зву­ка — качество звука, определяемое человеком субъективно на слух и зависящее от частоты звука. С ростом частоты высота звука увеличивается, т. е. звук становится «выше». Характер акустического спектра и распределения энергии между определен­ными частотами определяет своеобразие звукового ощущения, называемое тембром звука. Так, различные певцы, берущие одну и ту же ноту, имеют различный акустичес­кий спектр, т. е. их голоса имеют различный тембр.

Источником звука может быть всякое тело, колеблющееся в упругой среде со звуковой частотой (например, в струнных инструментах источником звука является струна, соединенная с корпусом инструмента).

Совершая колебания, тело вызывает колебания прилегающих к нему частиц среды с такой же частотой. Состояние колебательного движения последовательно передается к все более удаленным от тела частицам среды, т. е. в среде распространяется волна с частотой колебаний, равной частоте ее источника, и с определенной скоростью, зависящей от плотности и упругих свойств среды. Скорость распространения звуковых волн в газах вычисляется по формуле

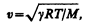(158.1)

где R — молярная газовая постоянная, М — молярная масса, g=С_р/С_V — отношение молярных теплоемкостей газа при постоянных давлении и объеме, Т — термодинами­ческая температура. Из формулы (158.1) вытекает, что скорость звука в газе не зависит от давления р газа, но возрастает с повышением температуры. Чем больше молярная масса газа, тем меньше в нем скорость звука. Например, при T =273 К скорость звука в воздухе (M =29×10^–3 кг/моль) v =331 м/с, в водороде (M =2×10^–3 кг/моль) v =1260 м/с. Выражение (158.1) соответствует опытным данным.

При распространении звука в атмосфере необходимо учитывать целый ряд фак­торов: скорость и направление ветра, влажность воздуха, молекулярную структуру газовой среды, явления преломления и отражения звука на границе двух сред. Кроме того, любая реальная среда обладает вязкостью, поэтому наблюдается затухание звука, т. е. уменьшение его амплитуды и, следовательно, интенсивности звуковой волны по мере ее распространения. Затухание звука обусловлено в значительной мере его поглощением в среде, связанным с необратимым переходом звуковой энергии в другие формы энергии (в основном в тепловую).

Для акустики помещений большое значение имеет реверберация звука — процесс постепенного затухания звука в закрытых помещениях после выключения его источ­ника. Если помещения пустые, то происходит медленное затухание звука и создается «гулкость» помещения. Если звуки затухают быстро (при применении звукопоглоща­ющих материалов), то они воспринимаются приглушенными. Время реверберации — это время, в течение которого интенсивность звука в помещении ослабляется в миллион раз, а его уровень — на 60 дБ. Помещение обладает хорошей акустикой, если время реверберации составляет 0,5—1,5 с.

S 159. Эффект Доплере в акустике

Эффектом Доплера* называется изменение частоты колебаний, воспринимаемой приемником, при движении источника этих колебаний и приемника друг относительно друга. Например, из опыта известно, что тон гудка поезда повышается по мере его приближения к платформе и понижается при удалении, т. е. движение источника колебаний (гудка) относительно приемника (уха) изменяет частоту принимаемых коле­баний.

* X. Доплер (1803—1853) — австрийский физик, математик и астроном.

Для рассмотрения эффекта Доплера предположим, что источник и приемник звука движутся вдоль соединяющей их прямой; v _ист и v _пр — соответственно скорости движе­ния источника и приемника, причем они положительны, если источник (приемник) приближается к приемнику (источнику), и отрицательны, если удаляется. Частота колебаний источника равна v ₀.

1. Источник и приемник покоятся относительно среды, т. е. v _ист = v _пр=0. Если v — скорость распространения звуковой волны в рассматриваемой среда, то длина волны l=vT=v/v ₀. Распространяясь в среде, волна достигнет приемника и вызовет колебания его звукочувствительного элемента с частотой

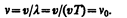
Следовательно, частота v звука, которую зарегистрирует приемник, равна частоте v ₀, с которой звуковая волна излучается источником.

2. Приемник приближается к источнику, а источник покоится, т. е. v _пр>0, v _ист=0. В данном случае скорость распространения волны относительно приемника станет равной v + v _пр. Так как длина волны при этом не меняется, то

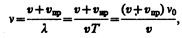
т. е. частота колебаний, воспринимаемых приемником, в (v+v _пр) /v раз больше частоты колебаний источника.

3. Источник приближается к преемнику, а приемник покоится, т. е. v _ист >0, v _пр=0.

Скорость распространения колебаний зависит лишь от свойств среды, поэтому за время, равное периоду колебаний источника, излученная им волна пройдет в направле­нии к приемнику расстояние vT (равное длине волны l) независимо от того, движется ли источник или покоится. За это же время источник пройдет в направлении волны расстояние v _ист T (рис. 224), т. е. длина волны в направлении движения сократится и станет равной l '= l — v _ист Т =(v — v _ист) T, тогда

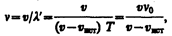
т. е. частота n колебаний, воспринимаемых приемником, увеличится в v /(v – v _ист) раз. В случаях 2 и 3, если v _ист<0 и v _пр<0, знак будет обратным.

4. Источник и приемник движутся относительно друг друга. Используя результаты, полученные для случаев 2 и 3, можно записать выражение для частоты колебаний, воспринимаемых приемником:

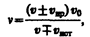(159.1)

причем верхний знак берется, если при движении источника или приемника происходит их сближение, нижний знак — в случае их взаимного удаления.

Из приведенных формул следует, что эффект Доплера различен в зависимости от того, движется ли источник или приемник. Если направления скоростей v _пр и v _ист не совпадают с проходящей через источник и приемник прямой, то вместо этих скоростей в формуле (159.1) надо брать их проекции на направление этой прямой.

§ 160. Ультразвук и его применение

По своей природе ультразвук представляет собой упругие волны, и в этом он не отличается от звука (см. § 158). Однако ультразвук, обладая высокими частотами (n >20 кГц) и, следовательно, малыми длинами волн, характеризуется особыми свойствами, что позволяет выделить его в отдельный класс явлений. Из-за малых длин волн ультразвуко­вые волны, как и свет, могут быть получены в виде строго направленных пучков. Для генерации ультразвука используются в основном два явления. Обратный пьезоэлектрический эффект (см. также § 91) — это возникновение дефор­мации в вырезанной определенным образом кварцевой пластинке (в последнее время вместо кварца применяется титанат бария) под действием электрического поля. Если такую пластинку поместить в высокочастотное переменное поле, то можно вызвать ее вынужденные колебания. При резонансе на собственной частоте пластинки получают большие амплитуды колебаний и, следовательно, большие интенсивности излучаемой ультразвуковой волны. Идея кварцевого ультразвукового генератора принадлежит французскому физику П. Ланжевену (1872—1946).

Магнитострикция — это возникновение деформации в ферромагнетиках под дейст­вием магнитного поля. Поместив ферромагнитный стержень (например, из никеля или железа) в быстропеременное магнитное поле, возбуждают его механические колебания, амплитуда которых максимальна в случае резонанса.

Ультразвуки широко используются в технике, например для направленной подводкой сигнализации, обнаружения подводных предметов и определения глубин (гидролока­тор, эхолот). Например, в эхолоте от пьезокварцевого генератора, укрепленного на судне, посылаются направленные ультразвуковые сигналы, которые, достигнув дна, отражаются от него и возвращаются обратно. Зная скорость их распространения в воде и определяя время прохождения (от подачи до возвращения) ультразвукового сигнала, можно вычислить глубину. Прием эха также производится с помощью пьезокварца. Звуковые колебания, дойдя да пьезокварца, вызывают в нем упругие колебания, в результате чего на противоположных поверхностях кварца возникают электрические заряды, которые измеряются.

Если пропускать ультразвуковой сигнал через исследуемую деталь, то можно обнаружить в ней дефекты по характерному рассеянию пучка и по появлению ультра­звуковой тени. На этом принципе создана целая отрасль техники — ультразвуковая дефектоскопия, начало которой положено С. Я. Соколовым (1897—1957). Применение ультразвука легло также в основу новой области акустики — акустоэлектроники, по­зволяющей на ее основе разрабатывать приборы для обработки сигнальной инфор­мации в микрорадиоэлектронике.

Ультразвук применяют для воздействия на различные процессы (кристаллизацию, диффузию, тепло- и массообмен в металлургии и т. д.) и биологические объекты (повышение интенсивности процессов обмена и т. д.), для изучения физических свойств веществ (поглощения, структуры вещества и т. д.). Ультразвук используется также для механической обработки очень твердых и очень хрупких тел, в медицине (диагностика, ультразвуковая хирургия, микромассаж тканей) и т. д.

19.1. Плоская гармоническая волна распространяется вдоль прямой, совпадающей с положи­тельным направлением оси х в среде, не поглощающей энергию, со скоростью v =12 м/с. Две точки, находящиеся на этой прямой на расстояниях x ₁ = 7 м и x ₂=12 м от источника колебаний, колеблются с разностью фаз D j = ⁵/₆ p. Амплитуда волны А = 6 см. Опреде­лить: 1) длину волны l; 2) уравнение волны; 3) смещение x ₂ второй точки в момент времени t = 3 с. [1) 12 см; 2) x (х, t) = 0,06 cos (2 pt – pх /6); 3) 6 см]

19.2. Два динамика расположены на расстоянии 2 м друг от друга и воспроизводят один и тот же музыкальный тон на частоте 1000 Гц. Приемник находится на расстоянии 4 м от центра динамиков. Принимая скорость звука 340 м/с, определить, на какое расстояние от центра­льной линии параллельно динамикам надо отодвинуть приемник, чтобы он зафиксировал первый интерференционный минимум. [0,34 м]

19.3. Для определения скорости звука в воздухе методом акустического резонанса исполь­зуется труба с поршнем и звуковой мембраной, закрывающей один из ее торцов. Расстоя­ние между соседними положениями поршня, при котором наблюдается резонанс на частоте 1700 Гц, составляет 10 см. Определить скорость звука в воздухе. [340 м/с]

19.4. Средняя квадратичная скорость молекул двухатомного газа при некоторых условиях составляет 461 м/с. Определить скорость распространения звука при тех же условиях. [315 м/с]

19.5. Поезд проходит со скоростью 54 км/ч мимо неподвижного приемника и подает звуковой сигнал. Приемник воспринимает скачок частоты D n = 54 Гц. Принимая скорость звука равной 340 м/с, определить частоту тона звукового сигнала гудка поезда. [611 Гц]

Глава 20Электромагнитные волны

§ 161. Экспериментальное получение электромагнитных волн

Существование электромагнитных волн — переменного электромагнитного поля, распространяющегося в пространстве с конечной скоростью, — вытекает из уравнений Максвелла (см. § 139). Уравнения Максвелла сформулированы в 1865 г. на основе обобщения эмпирических законов электрических и магнитных явлений. Как уже указы­валось, решающую роль для утверждения максвелловской теории сыграли опыты Герца (1888), доказавшие, что электрические и магнитные поля действительно рас­пространяются в виде воли, поведение которых полностью описывается уравнениями Максвелла.

Источником электромагнитных волн в действительности может быть любой элект­рический колебательный контур ила проводник, по которому течет переменный элект­рический ток, таккак для возбуждения электромагнитных волн необходимо создать в пространстве переменное электрическое поле (ток смещения) или соответственно переменное магнитное поле. Однако излучающая способность источника определяется его формой, размерами и частотой колебаний. Чтобы излучение играло заметную роль, необходимо увеличить объем пространства, в котором переменное электромаг­нитное поле создается. Поэтому для получения электромагнитных волн непригодны закрытые колебательные контуры, так как в них электрическое поле сосредоточено между обкладками конденсатора, а магнитное — внутри катушки индуктивности.

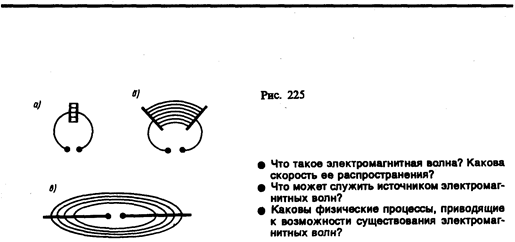
Герц в своих опытах, уменьшая число витков катушки и площадь пластин конден­сатора, а также раздвигая их (рис. 225, а, б), совершил переход от закрытого колеба­тельного контурак открытому колебательному контуру (вибратору Герца), представ­ляющему собой два стрежня, разделенных искровым промежутком (рис. 225, в). Если в закрытом колебательном контуре переменное электрическое поле сосредоточено внутри конденсатора (рис. 225, а), то в открытом оно заполняет окружающее контур пространство (рис. 255, в), что существенно повышает интенсивность электромагнит­ного излучения. Колебания в такой системе поддерживаются за счет источника э.д.с., подключенного к обкладкам конденсатора, а искровой промежуток применяется для того, чтобы увеличить разность потенциалов, до которой первоначально заряжаются обкладки.

Для возбуждения электромагнитных воли вибратор Герца В подключался к индуктору И (рис. 226). Когда напряжение на искровом промежутке достигало пробивного значения, возникала искра, закорачивающая обе половины вибратора, и в нем воз­никали свободные затухающие колебания. При исчезновении искры контур размыкался и колебания прекращались. Затем индуктор снова заряжал конденсатор, возникала искра и в контуре опять наблюдались колебания и т. д. Для регистрации электромаг­нитных воли Герц пользовался вторым вибратором, называемым резонатором Р, имеющим такую же частоту собственных колебаний, что и излучающий вибратор, т. е. настроенным в резонанс с вибратором. Когда электромагнитные волны достигали резонатора, то в его зазоре проскакивала электрическая искра.

С помощью описанного вибратора Герц экспериментировал с электромагнитными волнами, длина волны которых составляла примерно 3 м. П. Н. Лебедев, применяя миниатюрный вибратор из тонких платиновых стерженьков, получил миллиметровые электромагнитные волны с l = 6 – 4 мм. Дальнейшее развитие методики эксперимен­та в этом направлении позволило в 1923 г. российскому физику А. А. Глаголе­вой-Аркадьевой (1884—1945) сконструировать массовый излучатель, в котором корот­кие электромагнитные волны, возбуждаемые колебаниями электрических зарядов в атомах и молекулах, генерировались с помощью искр, проскакиваемых между металлическими опилками, взвешенными в масле. Так были получены волны с l от 50 мм до 80 мкм. Тем самым было доказано существование волн, перекрывающих интервал между радиоволнами и инфракрасным излучением.

Недостатком вибраторов Герца и Лебедева и массового излучателя Глаголе­вой-Аркадьевой являлось то, что свободные колебания в них быстро затухали и об­ладали малой мощностью. Для получения незатухающих колебаний необходимо со­здать автоколебательную систему (см. § 146), которая обеспечивала бы подачу энергии с частотой, равной частоте собственных колебаний контура. Поэтому в 20-х годах нашего столетия перешли к генерированию электромагнитных волн с помощью элект­ронных ламп. Ламповые генераторы позволяют получать колебания заданной (прак­тически любой) мощности и синусоидальной формы.

Электромагнитные волны, обладая широким диапазоном частот (или длин волн l = c / n, где с — скорость электромагнитных волн в вакууме), отличаются друг от друга по способам их генерации и регистрации, а также по своим свойствам. Поэтому электромагнитные волны делятся на несколько видов: радиоволны, световые волны, рентгеновское и g -излучения (табл.5). Следует отметить, что границы между различ­ными видами электромагнитных волн довольно условны.

Таблица 5

Продолжение табл. 5

§ 162. Дифференциальное уравнение электромагнитной волны

Как уже указывалось (см. § 161), одним из важнейших следствий уравнений Максвелла (см. § 139) является существование электромагнитных воли. Можно показать, что для однородной и изотропной среды вдали от зарядов и токов, создающих электромагнитное поле, из уравнений Максвелла следует, что векторы напряженностей Е и Н переменного электромагнитного поля удовлетворяют волновому уравнению типа (154.9):

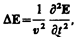(162.1)

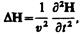(162.2)

где 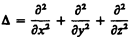— оператор Лапласа, v — фазовая скорость.

Всякая функция, удовлетворяющая уравнениям (162.1) и (162.2), описывает некото­рую волну. Следовательно, электромагнитные поля действительно могут существовать в виде электромагнитных волн. Фазовая скорость электромагнитных воли определяет­ся выражением

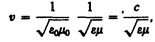(162.3)

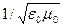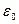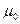где с = , и — соответственно электрическая и магнитная постоянные, e и m — соответственно электрическая и магнитная проницаемости среды.

В вакууме (при e =1 и m =l) скорость распространения электромагнитных волн совпадает со скоростью с. Так как em > 1, то скорость распространения электромагнит­ных воли в веществе всегда меньше, чем в вакууме.

При вычислении скорости распространения электромагнитного поля по формуле (162.3) получается результат, достаточно хорошо совпадающий с экспериментальными данными, если учитывать зависимость e и m от частоты. Совпадение же размерного коэффициента в (162.3) со скоростью распространения света в вакууме указывает на глубокую связь между электромагнитными и оптическими явлениями, позволившую Максвеллу создать электромагнитную теорию света, согласно которой свет представ­ляет собой электромагнитные волны.

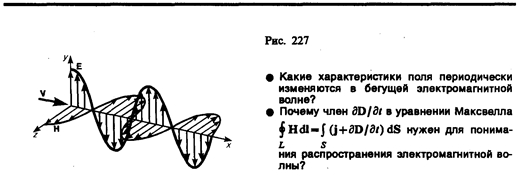
Следствием теории Максвелла является поперечность электромагнитных волн: век­торы Е и Н напряженностей электрического и магнитного полей волны взаимно перпендикулярны (на рис. 227 показана моментальная «фотография» плоской электро­магнитной волны) и лежат в плоскости, перпендикулярной вектору v скорости рас­пространения волны, причем векторы Е, Н и v образуют правовинтовую систему. Из уравнений Максвелла следует также, что в электромагнитной волне векторы Е и Н все­гда колеблются в одинаковых фазах (см. рис. 227), причем мгновенные значения Е и Н в любой точке связаны соотношением

(162.4)

Следовательно, Е и Н одновременно достигают максимума, одновременно обраща­ются в нуль и т. д. От уравнений (162.1) и (162.2) можно перейти к уравнениям

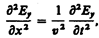(162.5)

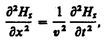(162.6)

где соответственно индексы у и z при Е и Н подчеркивают лишь то, что векторы Е и Н направлены вдоль взаимно перпендикулярных осей y и z.

Уравнениям (162.5) и (162.6) удовлетворяют, в частности, плоские монохроматические электромагнитные волны (электромагнитные волны одной строго определенной частоты), описываемые уравнениями

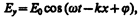(162.7)

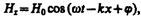(162.8)

где E ₀ и Н ₀ — соответственно амплитуды напряженностей электрического и магнит­ного полей волны, w — круговая частота волны, k=w/v — волновое число, j — на­чальные фазы колебаний в точках с координатой х= 0. В уравнениях (162.7) и (162.8) j одинаково, так как колебания электрического и магнитного векторов в электромаг­нитной волне происходят в одинаковых фазах.

§ 163. Энергия электромагнитных волн. Импульс электромагнитного поля

Возможность обнаружения электромагнитных воли указывает на то, что они переносят энергию. Объемная плотность w энергии электромагнитной волны складывается из объемных плотностей w _эл (см. (95.8)) и w _м, (см. (130.3)) электрического и магнитного полей:

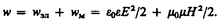
Учитывая выражение (162.4), получим, что плотности энергии электрического и маг­нитного полей в каждый момент времени одинаковы, т. е. w _эл = w _м. Поэтому

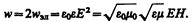
Умножив плотность энергии w на скорость v распространения волны в среде (см. (162.3)), получим модуль плотности потока энергии:

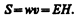
Tax как векторы Е и Н взаимно перпендикулярны и образуют с направлением распространения волны правовинтовую систему, то направление вектора [ ЕН ] совпада­ет с направлением переноса энергии, а модуль этого вектора равен ЕН. Вектор плотности потока электромагнитной энергии называется вектором Умова — Пойнтинга:

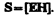
Вектор S направлен в сторону распространения электромагнитной волны, а его модуль равен энергии, переносимой электромагнитной волной за единицу времени через единичную площадку, перпендикулярную направлению распространения волны.

Если электромагнитные волны поглощаются или отражаются телами (эти явления подтверждены опытами Г. Герца), то из теории Максвелла следует, что электромаг­нитные волны должны оказывать на тела давление. Давление электромагнитных волн объясняется тем, что под действием электрического поля волны заряженные частицы вещества начинают упорядоченно двигаться и подвергаются со стороны магнитного поля волны действию сил Лоренца. Однако значение этого давления ничтожно мало. Можно оценить, что при средней мощности солнечного излучения, приходящего на Землю, давление для абсолютно поглощающей поверхности составляет примерно 5 мкПа. В исключительно тонких экспериментах, ставших классическими, П. Н. Лебе­дев в 1899 г. доказал существование светового давления на твердые тела, а в 1910 г. — на газы. Опыты Лебедева имели огромное значение для утверждения выводов теории Максвелла о том, что свет представляет собой электромагнитные волны.

Существование давления электромагнитных воли приводит к выводу о том, что электромагнитному полю присущ механический импульс. Импульс электрома­гнитного поля

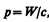
где W — энергия электромагнитного поля. Выражая импульс как р=тс (поле в ваку­уме распространяется со скоростью с), получим р=тс= W/c, откуда

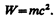(163.1)

Это соотношение между массой и энергией электромагнитного поля является универ­сальным законом природы (см. также § 40). Согласно специальной теории относитель­ности, выражение (163.1) имеет общее значение и справедливо для любых тел независи­мо от их внутреннего строения.

Таким образом, рассмотренные свойства электромагнитных волн, определяемые теорией Максвелла, полностью подтверждаются опытами Герца, Лебедева и выводами специальной теории относительности, сыгравшими решающую роль для подтвержде­ния и быстрого признания этой теории.

§ 164. Излучение диполя. Применение электромагнитных волн

Простейшим излучателем электромагнитных волн является электрический диполь, электрический момент которого изменяется во времени по гармоническому закону

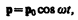
где р ₀ — амплитуда вектора р. Примером подобного диполя может служить система, состоящая из покоящегося положительного заряда + Q и отрицательного заряда –Q, гармонически колеблющегося вдоль направления р с частотой w.

Задача об излучении диполя имеет в теории излучающих систем важное значение, так как всякую реальную излучающую систему (например, антенну) можно рассчиты­вать рассматривая излучение диполя. Кроме того, многие вопросы взаимодействия излучения с веществом можно объяснить на основе классической теории, рассматривая атомы как системы зарядов, в которых электроны совершают гармонические колеба­ния около их положений равновесия.

Дата добавления: 2014-11-25