КУРС ФИЗИКИ 26 страница

Автоколебания принципиально отличаются от свободных незатухающих колебаний, происходящих без действия сил, а также от вынужденных колебаний (см. § 147), происходящих под действием периодической силы. Автоколебательная система сама управляет внешними воздействиями, обеспечивая согласованность поступления энер­гии определенными порциями в нужный момент времени (в такт с ее колебаниями).

Примером автоколебательной системы могут служить часы. Храповой механизм подталкивает маятник в такт с его колебаниями. Энергия, передаваемая при этом маятнику, берется либо за счет раскручивающейся пружины, либо за счет опуска­ющегося груза. Колебания воздуха в духовых инструментах и органных трубах также возникают вследствие автоколебаний, поддерживаемых воздушной струёй.

Автоколебательными системами являются также двигатели внутреннего сгорания, паровые турбины, ламповый генератор и т. д.

§ 147. Дифференциальное уравнение вынужденных колебаний (механических и электромагнитных) и его решение

Чтобы в реальной колебательной системе получить незатухающие колебания, надо компенсировать потери энергии. Такая компенсация возможна с помощью какого-либо периодически действующего фактора X (t), изменяющего по гармоническому закону:

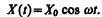
Если рассматривать механические колебания, то роль X (t) играет внешняя вынуж­дающая сила

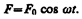(147.1)

С учетом (147.1) закон движения для пружинного маятника (146.9) запишется в виде

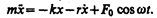
Используя (142.2) и (146.10), придем к уравнению

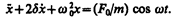(147.2)

Если рассматривать электрический колебательный контур, то роль X (t) играет подводимая к контуру внешняя периодически изменяющаяся по гармоническому закону э.д.с. или переменное напряжение

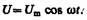(147.3)

Тогда уравнение (143.2) с учетом (147.3) можно записать в виде

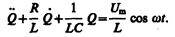
Используя (143.4) и (146.11), придем к уравнению

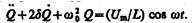(147.4)

Колебания, возникающие под действием внешней периодически изменяющейся силы или внешней периодически изменяющейся э.д.с., называются соответственно вынужденными механическими и вынужденными электромагнитными колебаниями.

Уравнения (147.2) и (147.4) можно свести к линейному неоднородному дифференци­альному уравнению

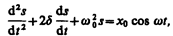(147.5)

применяя впоследствии его решение для вынужденных колебаний конкретной физичес­кой природы (x ₀ в случае механических колебаний равно F ₀ /m, в случае электромагнит­ных — U _m/ L).

Решение уравнения (147.5) равно сумме общего решения (146.5) однородного урав­нения (146.1) и частного решения неоднородного уравнения. Частное решение найдем в комплексной форме (см. § 140). Заменим правую часть уравнения (147.5) на комплексную величину х ₀ :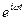

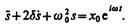(147.6)

Частное решение этого уравнения будем искать в виде

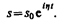
Подставляя выражение для s и его производных 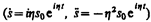в уравнение (147.6), получаем

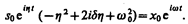(147.7)

Так как это равенство должно быть справедливым для всех моментов времени, то время t из него должно исключаться. Отсюда следует, что h=w. Учитывая это, из уравнения (147.7) найдем величину s ₀ и умножим ее числитель и знаменатель на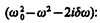

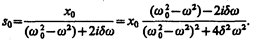
Это комплексное число удобно представить в экспоненциальной форме:

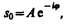
где

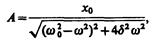(147.8)

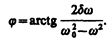(147.9)

Следовательно, решение уравнения (147.6) в комплексной форме примет вид

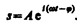
Его вещественная часть, являющаяся решением уравнения (147.5), равна

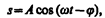(147.10)

где А и j задаются соответственно формулами (147.8) и (147.9).

Таким образом, частное решение неоднородного уравнения (147.5) имеет вид

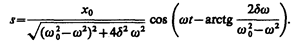(147.11)

Решение уравнения (147.5) равно сумме общего решения однородного уравнения

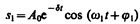(147.12)

(см. (146.5)) и частного решения (147.11). Слагаемое (147.12) играет существенную роль только в начальной стадии процесса (при установлении колебаний) до тех пор, пока амплитуда вынужденных колебаний не достигнет значения, определяемого равенством (147.8). Графически вынужденные колебания представлены на рис. 209. Следовательно, в установившемся режиме вынужденные колебания происходят с частотой w и являют­ся гармоническими; амплитуда и фаза колебаний, определяемые выражениями (147.8) и (147.9), также зависят от w.

Запишем формулы (147.10), (147.8) и (147.9) для электромагнитных колебаний, учитывая, что 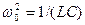(см. (143.4)) и 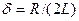(см. (146.11)):

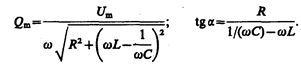(147.13)

Продифференцировав Q=Q _mcos(wt–a) по t, найдем силу тока в контуре при устано­вившихся колебаниях:

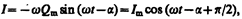(147.14)

где

(147.15)

Выражение (147.14) может быть записано в ввде

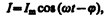
где j = a – p /2 — сдвиг по фазе между током и приложенным напряжением (см. (147.3)). В соответствии с выражением (147.13)

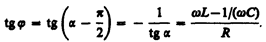(147.16)

Из формулы (147.16) вытекает, что ток отстает по фазе от напряжения (j> 0), если wL> 1/(w С), и опережает напряжение (j< 0), если wL< 1/(w С).

Формулы (147.15) и (147.16) можно также получить с помощью векторной диаграм­мы. Это сделано в §149 для переменных токов.

§ 148. Амплитуда и фаза вынужденных колебаний (механических и электромагнитных). Резонанс

Рассмотрим зависимость амплитуды А вынужденных колебаний от частоты w. Меха­нические и электромагнитные колебания будем рассматривать одновременно, называя колеблющуюся величину либо смещением (х) колеблющегося тела из положения равновесия, либо зарядом (Q) конденсатора.

Из формулы (147.8) следует, что амплитуда А смещения (заряда) имеет максимум. Чтобы определить резонансную частоту w _рез, — частоту, при которой амплитуда А сме­щения (заряда) достигает максимума, — нужно найти максимум функции (147.8), или, что то же самое, минимум подкоренного выражения. Продифференцировав подкорен­ное выражение по w и приравняв его нулю, получим условие, определяющее w _рез:

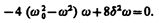
Это равенство выполняется при w =0, ± 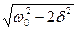, у которых только лишь положи­тельное значение имеет физический смысл. Следовательно, резонансная частота

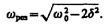(148.1)

Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы (частоты вынуждающего переменного напряжения) к ча­стоте, равной или близкой собственной частоте колебательной системы, называется резонансом (соответственно механическим или электрическим). При значение w _рез практически совпадает с собственной частотой w ₀ колебательной системы. Подста­вляя (148.1) в формулу (147.8), получим

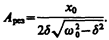(148.2)

На рис. 210 приведены зависимости амплитуды вынужденных колебаний от часто­ты при различных значениях d. Из (148.1) и (148.2) вытекает, что чем меньше d, тем выше и правее лежит максимум данной кривой. Если w ® 0, то все кривые (см. также (147.8)) достигают одного в того же, отличного от нуля, предельного значения 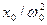, которое называют статическим отклонением. В случае механических колебаний 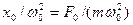, в случае электромагнитных – U _m / (L 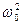). Если w ®¥, то вое кривые асимптотически стремятся к нулю. Приведенная совокупность кривых называется резонансными кривыми.

Из формулы (148.2) вытекает, что при малом затухании () резонансная амплитуда смещения (заряда)

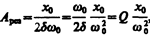
где Q — добротность колебательной системы (см. (146.8)), 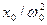— рассмотренное выше статическое отклонение. Отсюда следует, что добротность Q характеризует резонансные свойства колебательной системы: чем больше Q, тем больше А _рез.

На рис. 211 представлены резонансные кривые для амплитуды скорости (тока). Амплитуда скорости (тока)

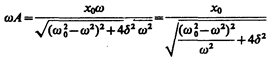
максимальна при w _рез =w ₀ и равна 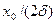, т. е. чем больше коэффициент затухания d, тем ниже максимум резонансной кривой. Используя формулы (142.2), (146.10) и (143.4), (146.11), получим, что амплитуда скорости при механическом резонансе равна

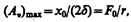
а амплитуда тока при электрическом резонансе

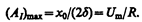
Из выражения tg j = 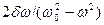(см. (147.9)) следует, что если затухание в системе отсутствует (d= 0), то только в этом случае колебания и вынуждающая сила (прило­женное переменное напряжение) имеют одинаковые фазы; во всех других случаях j ¹0.

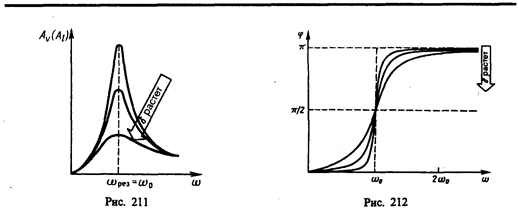
Зависимость j от w при разных коэффициентах d графически представлена на рис. 212, из которого следует, что при изменении w изменяется и сдвиг фаз j. Из формулы (147.9) вытекает, что при w =0 j =0, а при w = w ₀ независимо от значения коэффициента затухания j = p /2, т. е. сила (напряжение) опережает по фазе колебания на p /2. При дальнейшем увеличении w сдвиг фаз возрастает и при w >> w ₀ j ® p, т. е. фаза колебаний почти противоположна фазе внешней силы (переменного напряжения). Семейство кривых, изображенных на рис. 212, называется фазовыми резонансными кривыми.

Явления резонанса могут быть как вредными, так и полезными. Например, при конструировании машин и различного рода сооружений необходимо, чтобы собствен­ная частота колебаний их не совпадала с частотой возможных внешних воздействий, в противном случае возникнут вибрации, которые могут вызвать серьезные разруше­ния. С другой стороны, наличие резонанса позволяет обнаружить даже очень слабые колебания, если их частота совпадает с частотой собственных колебаний прибора. Так, радиотехника, прикладная акустика, электротехника используют явление резонанса.

§ 148. Переменный ток

Установившиеся вынужденные электромагнитные колебания (см. § 147) можно рас­сматривать как протекание в цепи, содержащей резистор, катушку индуктивности и конденсатор, переменного тока. Переменный ток можно считать квазистационарным, т. е. для него мгновенные значения силы тока во всех сечениях цепи практически одинаковы, таккак их изменения происходят достаточно медленно, а электромагнит­ные возмущения распространяются по цепи со скоростью, равной скорости света. Для мгновенных значений квазистационарных токов выполняются закон Ома и вытека­ющие из него правила Кирхгофа, которые будут использованы применительно к пере­менным токам (эти законы уже использовались при рассмотрении электромагнитных колебаний).

Рассмотрим последовательно процессы, происходящие на участке цепи, содер­жащем резистор, катушку индуктивности и конденсатор, к концам которого приложено переменное напряжение

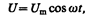(149.1)

где U _m — амплитуда напряжения.

1. Переменный ток, текущий через резистор сопротивлением R (L ®0, C ®0) (рис. 213, а). При выполнении условия квазистационарности ток через резистор опреде­ляется законом Ома:

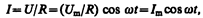
где амплитуда силы тока I _m= U _m /R.

Для наглядного изображения соотношений между переменными токами и напряже­ниями воспользуемся методом векторных диаграмм. На рис. 213, б дана векторная диаграмма амплитудных значений тока I _m и напряжения U _m на резисторе (сдвиг фаз между I _m и U _m равен нулю).

2. Переменный ток, текущий через катушку индуктивностью L (R ®0, C ®0) (рис. 214, а). Если в цепи приложено переменное напряжение (149.1), то в ней потечет переменный ток, в результате чего возникнет э.д.с. самоиндукции (см. (126.3)) 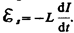. Тогда закон Ома (см. (100.3)) для рассматриваемого участка цепи имеет вид

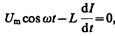
откуда

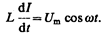(149.2)

Таккак внешнее напряжение приложено к катушке индуктивности, то

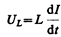(149.3)

есть падение напряжения на катушке. Из уравнения (149.2) следует, что

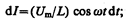
после интегрирования, учитывая, что постоянная интегрирования равна нулю (так как отсутствует постоянная составляющая тока), получим

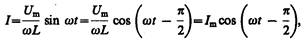(149.4)

где I _m= U _m/(wL). Величина

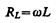(149.5)

называется реактивным индуктивным сопротивлением (или индуктивным сопротивлени­ем). Из выражения (149.5) вытекает, что для постоянного тока (w = 0) катушка индук­тивности не имеет сопротивления. Подстановка значения U _m =wLI _m в выражение (149.2) с учетом (149.3) приводит к следующему значению падения напряжения на катушке индуктивности:

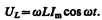(149.6)

Сравнение выражений (149.4) и (149.6) приводит к выводу, что падение напряжения U_L опережает по фазе ток I, текущий через катушку, на p /2, что и показано на векторной диаграмме (рис. 214, б).

3. Переменный ток, текущий через конденсатор емкостью С (R ®0, L ®0) (рис. 215, в). Если переменное напряжение (149.1) приложено к конденсатору, то он все время перезаряжается, и в цепи течет переменный ток. Так как все внешнее напряжение приложено к конденсатору, а сопротивлением подводящих проводов можно пренеб­речь, то

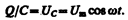
Сила тока

(149.7)

где

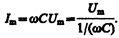
Величина

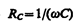
называется реактивным емкостным сопротивлением (или емкостным сопротивлением). Для постоянного тока (w = 0) R_С = ¥, т. е. постоянный ток через конденсатор течь не может. Падение напряжения на конденсаторе

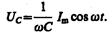(149.8)

Сравнение выражений (149.7) и (149.8) приводит к выводу, что падение напряжения U_С отстает по фазе от текущего через конденсатор тока I на p /2. Это показано на векторной диаграмме (рис. 215, б).

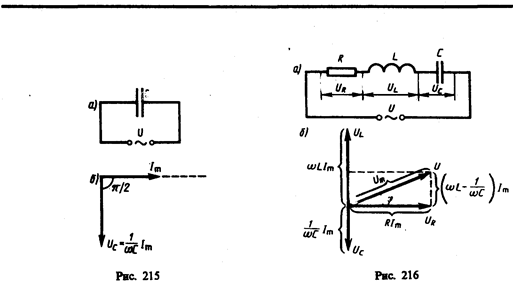
4. Цепь переменного тока, содержащая последовательно включенные резистор, ка­тушку индуктивности и конденсатор. На рис. 216, а представлен участок цепи, содер­жащий резистор сопротивлением R, катушку индуктивностью L и конденсатор ем­костью С, к концам которого приложено переменное напряжение (149.1). В цепи возникнет переменный ток, который вызовет на всех элементах цепи соответствующие падения напряжения U_R, U_L и U_C. На рис. 216, б представлена векторная диаграмма амплитуд падений напряжений на резисторе (U_R), катушке (U_L) и конденсаторе (U_C). Амплитуда U _m приложенного напряжения должна быть равна векторной сумме амп­литуд этих падений напряжений. Как видно из рис. 216, б, угол j определяет разность фаз между напряжением и силой тока. Из рисунка следует, что (см. также формулу (147.16))

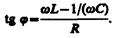(149.9)

Из прямоугольного треугольника получаем 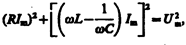откуда ам­плитуда силы тока имеет значение

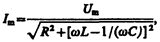(149.10)

совпадающее с (147.15).

Следовательно, если напряжение в цепи изменяется по закону U = U _m cos w t, то в цепи течет ток

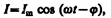(149.11)

где j и I _m определяются соответственно формулами (149.9) и (149.10). Величина

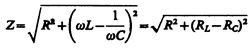(149.12)

называется полным сопротивлением цепи, а величина

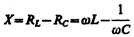
– реактивным сопротивлением.

Рассмотрим частный случай, когда в цепи отсутствует конденсатор. В данном случае падения напряжений U_R и U_L в сумме равны приложенному напряжению U. Векторная диаграмма для данного случая представлена на рис. 217, из которого следует, что

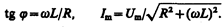(149.13)

Выражения (149.9) и (149.10) совпадают с (149.13), если в них 1/(wC) = 0, т.е. С =¥. Следовательно, отсутствие конденсатора в цепи означает С =¥, а не С= 0. Данный вывод можно трактовать следующим образом: сближая обкладки конденсатора до их полного соприкосновения, получим цепь, в которой конденсатор отсутствует (расстоя­ние между обкладками стремится к нулю, а емкость — к бесконечности; см. (94.3)).

§ 150. Резонанс напряжений

Если в цепи переменного тока, содержащей последовательно включенные конденсатор, катушку индуктивности и резистор (см. рис. 216),

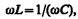(150.1)

то угол сдвига фаз между током и напряжением (149.9) обращается в нуль (j =0), т. е. изменения тока и напряжения происходят синфазно. Условию (150.1) удовлетворяет частота

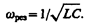(150.2)

В данном случае полное сопротивление цепи Z (149.12) становится минимальным, равным активному сопротивлению R цепи, и ток в цепи определяется этим сопротивле­нием, принимая максимальные (возможные при данном U _m) значения. При этом падение напряжения на активном сопротивлении равно внешнему напряжению, прило­женному к цепи (U_R = U), а падения напряжений на конденсаторе (U_C) и катушке индуктивности (U_L) одинаковы по амплитуде и противоположны по фазе. Это явление называется резонансом напряжений (последовательным резонансом), а частота (150.2) — резонансной частотой. Векторная диаграмма для резонанса напряжений при­ведена на рис. 218, а зависимость амплитуды силы тока от w уже была дана на рис. 211.

В случае резонанса напряжений

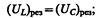
подставив в эту формулу значения резонансной частоты и амплитуды напряжений на катушке индуктивности и конденсаторе, получим

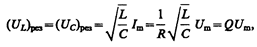
где Q — добротность контура, определяемая выражением (146.14). Так как доброт­ность обычных колебательных контуров больше единицы, то напряжение как на катушке индуктивности, так и на конденсаторе превышает напряжение, приложенное к цепи. Поэтому явление резонанса напряжений используется в технике для усиления колебания напряжения какой-либо определенной частоты. Например, в случае резонан­са на конденсаторе можно получить напряжение с амплитудой QU _m (Q в данном случае—добротность контура, которая может быть значительно больше U _m). Это усиление напряжения возможно только для узкого интервала частот вблизи резонанс­ной частоты контура, что позволяет выделить из многих сигналов одно колебание определенной частоты, т. е. на радиоприемнике настроиться на нужную длину волны. Явление резонанса напряжений необходимо учитывать при расчете изоляции элект­рических линий, содержащих конденсаторы и катушки индуктивности, так как иначе может наблюдаться их пробой.

§ 151. Резонанс токов

Рассмотрим цепь переменного тока, содержащую параллельно включенные конден­сатор емкостью С и катушку индуктивностью L (рис. 219). Для простоты допустим, что активное сопротивление обеих ветвей настолько мало, что им можно пренебречь. Если приложенное напряжение изменяется по закону U= U _m сos w t (см. (149.1)), то, согласно формуле (149.11),в ветви 1С2 течет ток

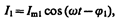
амплитуда которого определяется из выражения (149.10) при условии R= 0 и L =0:

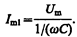
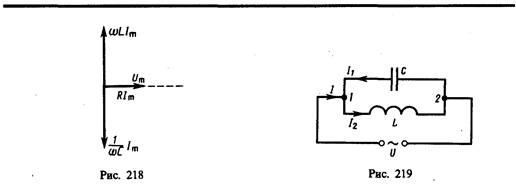
Начальная фаза j ₁ этого тока по формуле (149.9) определяется равенством

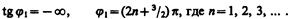(151.1)

Аналогично, сила тока в ветви 1L2

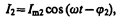
амплитуда которого определяется из (149.10) при условии R= 0 и С =¥ (условие отсутствия емкости в цепи, см. § 149):

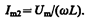
Начальная фаза j ₂ этого тока (см. (149.9))

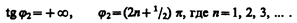(151.2)

Из сравнения выражений (151.1) и (151.2) вытекает, что разность фаз токов в ветвях 1С2 н 1L2 равна j ₁ —j ₂ =p, т. е. токи в ветвях противоположны по фазе. Амплитуда силы тока во внешней (неразветвленной) цепи

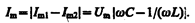
Если w = w _рез = , то I _m1= I _m2и I _m=0. Явление резкого уменьшения амплитуды силы тока во внешней цепи, питающей параллельно включенные конденсатор и катуш­ку индуктивности, при приближении частоты w приложенного напряжения к резонанс­ной частоте w _рез называется резонансом токов (параллельным резонансом). В данном случае для резонансной частоты получили такое же значение, как и при резонансе напряжений (см. § 150).

Амплитуда силы тока I _m оказалась равна нулю потому, что активным сопротивле­нием контура пренебрегли. Если учесть сопротивление R, то разность фаз j ₁ —j ₂будет равна p, поэтому при резонансе токов амплитуда силы тока I _m будет отлична от нуля, но примет наименьшее возможное значение. Таким образом, при резонансе токов во внешней цепи токи I ₁ и I ₂ компенсируются и сила тока I в подводящих проводах достигает минимального значения, обусловленного только током через резистор. При резонансе токов силы токов I ₁ и I ₂ могут значительно превышать силу тока I.

Рассмотренный контур оказывает большое сопротивление переменному току с ча­стотой, близкой к резонансной. Поэтому это свойство резонанса токов используется в резонансных усилителях, позволяющих выделять одно определенное колебание из сигнала сложной формы. Кроме того, резонанс токов используется в индукционных печах, где нагревание металлов производится вихревыми токами (см. § 125). В них емкость конденсатора, включенного параллельно нагревательной катушке, подбирает­ся так, чтобы при частоте генератора получился резонанс токов, в результате чего сила тока через нагревательную катушку будет гораздо больше, чем сила тока в подводя­щих проводах.

§ 152. Мощность, выделяемая в цепи переменного тока

Мгновенное значение мощности переменного тока равно произведению мгновенных значений напряжения и силы тока:

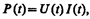
где U(t)=U _mcos wt, I(t)=I _mcos(wt – j) (см. выражения (149.1) и (149.11)). Раскрыв cos(wt – j), получим

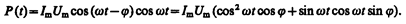
Практический интерес представляет не мгновенное значение мощности, а ее среднее значение за период колебания. Учитывая, что ácos² w t ñ= ¹/₂, ásin w t cos w t ñ = 0, получим

Дата добавления: 2014-11-25